НОУ ИНТУИТ | Лекция | Числа

Аннотация: В лекции подробно рассмотрена работа с числами — целыми и вещественными, знаковыми и беззнаковыми. Дан материал по различным операциям с числами, их преобразовании в другие типы данных, вывод на экран в нужном формате. Материал закрепляется практикой — созданием программы для определения Индекса Массы Тела.

Цель лекции

Получение знаний по работе с числами всех типов, преобразование чисел в другие типы данных, закрепление материала на практике.

Целые числа

В Lazarus (а точнее, в Free Pascal), как и в любом другом языке программирования, числа играют довольно важную роль. Трудно представить себе программу, в которой не использовались бы числа. Даже когда вы просто установите какой-то компонент на форму, автоматически начинают действовать множество настроек. Left, Top, Height, Width — все эти свойства есть в любом визуальном компоненте, и они содержат числа. Числа бывают целые и вещественные, знаковые и беззнаковые.

В этом разделе поговорим о целых числах, как знаковых, так и беззнаковых. Что такое целое число? Это число без запятой, то есть, без десятичной части. Знаковым называют число со знаком: -1, например. Беззнаковое число — это число от нуля и больше.

В программировании базовым целым числом является integer, который мы уже не раз использовали. Но вы, вероятно, догадались, что это не единственный возможный целый тип? Есть разные типы целых чисел, они могут быть со знаком и без него, имеют разный диапазон возможных значений и, соответственно, занимают разный размер оперативной памяти. Разберем эти типы:

Таблица 8.1. Целые числа

Тип	Диапазон	Размер в байтах
Byte	0…255	1
ShortInt	-128…127	1
Word	0…65 535	2
Smallint	-32 768…32 767	2
LongWord	0…4 294 967 295	4
Cardinal	0…4 294 967 295	4
LongInt	-2 147 483 648…2 147 483 647	4
Integer	-2 147 483 648…2 147 483 647	4
Int64		8

intuit.ru/2010/edi»>Обратите внимание, здесь диапазон и размер Integer совпадает с LongInt. Вообще-то, это зависит от режима компилятора FPC. Проект можно скомпилировать в разных режимах, с поддержкой Delphi, например, или TP (Turbo Pascal). По умолчанию, выставлен режим Object Pascal, это можно проверить, выполнив в среде Lazarus команду меню Проект -> Параметры проекта, затем в разделе Параметры компилятора выбрать Обработка. В верхней части там указан Режим синтаксиса, по умолчанию это Object Pascal, но при необходимости его можно и поменять.

Так вот, если там выставлен режим Object Pascal или Delphi, тогда Integer имеет размер 32 бита, или 4 байта. Если же выставлен старый режим Turbo Pascal или Free Pascal, то Integer будет иметь размер в 16 бит или 2 байта, и будет соответствовать типу Smallint.

Зачем нужно такое разнообразие целых типов? В былые времена оперативная память была довольно маленькой.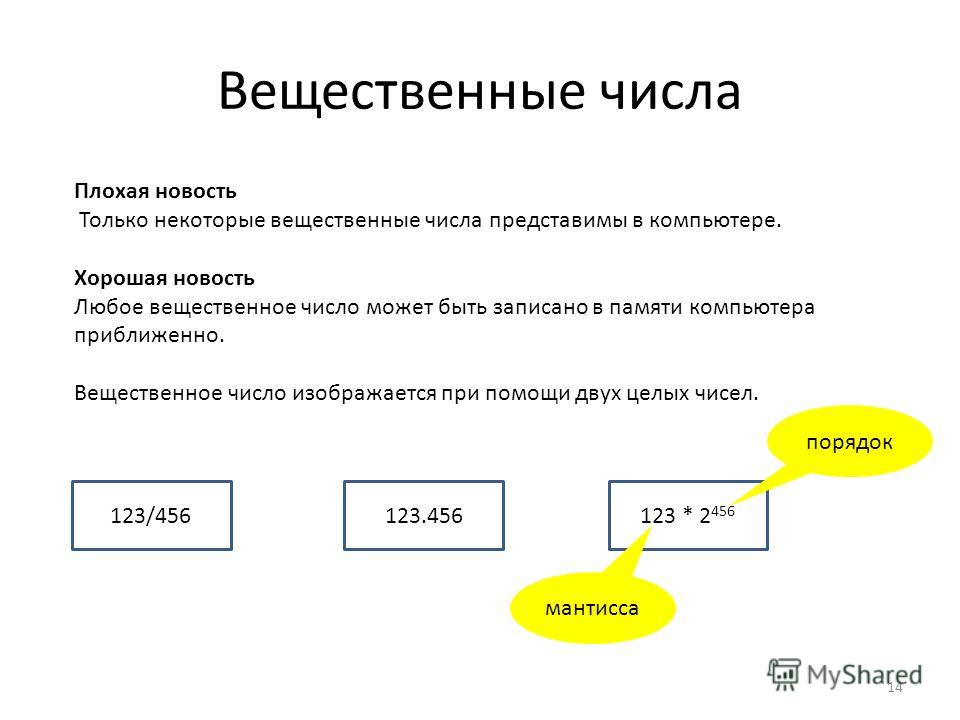 Если сейчас у меня на ПК установлена оперативная память 4 Гб, то когда-то давно я был вынужден обходиться компьютером с процессором 486 и оперативкой аж в 16 мегабайт, и можете поверить, это был далеко не самый худший компьютер! В те времена программисты сражались за каждый байт памяти, переписывая и минимизируя код, выбирая самые маленькие из возможных типы данных. Это называлось оптимизацией кода. Допустим, вам нужно выполнить какой-то цикл 10 раз. Для подсчета шагов цикла вам придется создать переменную целого типа. Но зачем использовать переменную Integer в 4 байта, когда вполне можно обойтись однобайтовым Byte? Сейчас конечно, это не играет такой большой роли, как прежде, но всё равно, оптимизация кода — это признак хорошего программиста, это хороший тон в программировании. Так что старайтесь не тратить понапрасну лишнюю память.

Рекомендации тут следующие: если вы знаете, что число будет без знака, то и выбирайте беззнаковые типы.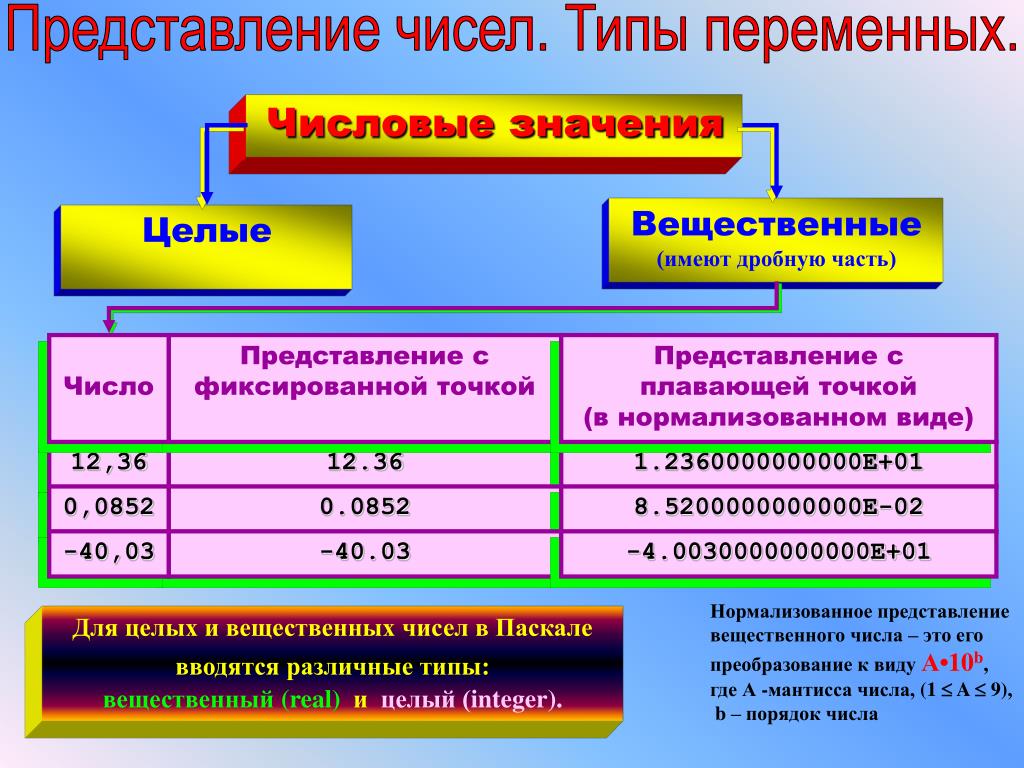 Если вы точно знаете, что максимальное число в переменной будет маленьким, выбирайте типы поменьше. Если вам неизвестно, какого размера число попадет в переменную, то выбирайте Integer — это универсальный тип, годный для большинства случаев. Ну а если вы уверены, что число будет очень большим, то используйте 4-х или даже 8-ми байтовые типы.

Вещественные числа

Вещественными называются числа с дробной частью, причем, если дробная часть равна нулю, её все равно нужно указать. Например:

Такие числа еще называют числами с плавающей точкой

, поскольку количество цифр после точки может быть различным. Записываются вещественные числа по определенным правилам. Если в математике мы дробную часть отделяем запятой, в Lazarus для этого используют точку. При указании очень большого числа можно выбрать сокращенную форму. Если в математике для этого число умножают на десятичную степень, например,

intuit.ru/2010/edi»>то в Lazarus вместо 10 указывают букву E (от англ. exponent — показатель степени):

Степени могут быть и отрицательными:

Вещественных типов тоже много. В характеристике вещественных чисел роль играет не только размер, занимаемый в памяти, но и количество значащих цифр:

Таблица 8.2. Вещественные числа

Тип	Диапазон	Количество значащих цифр	Размер в байтах
Single	1.5E-45…3.4E38	7-8	4
Real	5. 0E-324…1.7E308	15-16	8
Double	5.0E-324…1.7E308	15-16	8
Comp	-2E64+1…2E63-1	19-20	8
Currency	-922 337 203 685 477.5808 … 922 337 203 685 477.5807	19-20	8
Extended	1.9E-4932…1.1E4932	19-20	10

Как видите, вещественные числа куда больше целых, процессорного времени на обработку таких чисел тратится тоже больше. Поэтому вещественные числа имеет смысл применять только по необходимости, когда целыми числами явно не обойтись. Не слушайте тех, кто предлагает на все случаи жизни использовать тип Real — и для целых, и для вещественных чисел.

Рекомендации тут такие же, как и для целых чисел — выбирайте типы по необходимости. Особо выделю тип Currency — его создали специально для финансовых расчетов, поэтому для всякого рода бухгалтерских расчетов лучше выбирать именно этот тип, как наиболее точный. Но чаще всего обходятся типом Real (или Double).

Операции над целыми и вещественными числами

Целые числа можно складывать (+), отнимать (-) и умножать (*) друг на друга. С делением дело обстоит сложней. Допустим, нам нужно 10 разделить на 3. Получится 3,33333…, а это уже не целое число. Поэтому для целых чисел в Паскале предусмотрено деление нацело. Операция div обеспечивает деление нацело, и возвращает целую часть, отбрасывая дробную. Например, 10 разделить на 8 будет равно 1,25. Если применить целочисленное деление, то 10 div 8 = 1. Чтобы узнать остаток от такого деления, применяют операцию mod. 10 mod 8 = 2.

Арифметика над вещественными числами еще проще, здесь применяют следующие стандартные операции: + (сложение), — (вычитание), * (умножение), / (деление).

Кроме того, как целые, так и вещественные числа можно сравнивать между собой, используя для этого логические операторы: = (равно), <> (не равно), > (больше), < (меньше), >= (больше или равно), <= (меньше или равно).

Очень часто приходится использовать большие и сложные выражения, где вместе с арифметическими используются и логические операторы. Здесь главное — не забывать о приоритетах. Возьмем выражение

Что попадет в переменную r? Если вы ответили 11, то вы правы.

Чтобы сначала выполнить сложение, его нужно поместить в скобки, которые имеют высший приоритет:

В этом случае, в переменную r попадет число 14.

Таблица 8.3. Приоритеты

Порядок	Операции
1	( ) — То, что в круглых скобках, вычисляется в первую очередь
2	NOT
3	*, /, DIV, MOD, AND
4	+, -, OR, XOR
5	=, <>, >, <, >=, <=

Примечание: Если в выражении встречаются операции одинакового приоритета, они выполняются слева — направо.

Примечание: Ни целое, ни вещественное число НЕЛЬЗЯ ДЕЛИТЬ НА НОЛЬ! Если такое произойдет, возникнет Исключительная ситуация, и будет выведена ошибка. Программисты обычно всегда проверяют, что и на что пользователь делит. Если он пытается делить на ноль, выводится понятное сообщение об ошибке, а само деление не производится. Это называется «защита от дурака».

1.6 Переменные и константы [Оберон / Компонентный Паскаль / Вики]

1.6 Переменные и константы

1. Типы данных

Под понятием Тип данных скрывается семантическое свойство информации. Для компьютера все байты информации представляют из себя пакеты из 8 бит. Каждый из битов может быть включенным или выключенным. В зависимости от того, как принято понимать эти состояния (прямая или инверсная логика) — эти значения принимаются равными «0» или «1». Больше о содержимом ячеек памяти компьютер не знает ничего.

Но для программиста даже один байт может содержать различные типы информации. Например, 8 бит (= 1 байт), с точки зрения программиста — может содержать числа от 0 до 255. А может и код символа в однобайтовой кодировке («а», «б», «в»…). А может и вообще что-то иное. Но все байты одинаковы, у них нет признака того, что они хранят. В какой-то момент, программист вполне может решить, что вот эта ячейка памяти хранит число от 0 до 255¹⁾. А на самом деле, в самом начале, программист задумывал хранить в этой ячейке памяти код символа для последующей печати. Более того, вполне может быть, что программист решил использовать под свои нужды не одну, а сразу две (или даже тысячу) ячеек? Помнить где расположена каждая ячейка? Такое программирование превратится в ад! И такие ошибки встречаются и у новичков, и у опытных программистов. Как решить эту проблему?

Проблема решается тем, что помнить о том, где расположена каждая ячейка памяти, и что она хранит — должен Компонентный Паскаль. Этой информации нет в самой ячейке, зато есть у языка программирования. Это и есть семантическое свойство информации, в данном случае — её тип. Таким образом описанная ячейка называется «переменная». Свой тип она не меняет с момента её описания, до момента окончания выполнения программы. Исключений не бывает²⁾.

2. Целые числа

2.1 Логический тип

Логический тип, в полном смысле этого слова не является целым. Но и к дробным числам этот тип можно отнести ещё меньше. Переменная такого типа может принимать только два значения. В Компонентном Паскале эти два значения определены как TRUE («Истина») и FALSE («Ложь»). Этот тип переменных используется даже шире, чем об этом задумываются многие программисты. Логический тип можно использовать явно (через переменную), а можно и неявно (например, через сравнение двух чисел, строк, результатов вызовов процедур). Обозначается такой тип через ключевое слово BOOLEAN. Пример:

бНоль: BOOLEAN; (* флаг признака нуля *)
бСепар: BOOLEAN; (* сепаратор; отвечает за разделение глав *)

Стоит обратить внимание на выравнивание двоеточий и ключевых слов. Двоеточие, если проводить аналогию с русским языком может выступать как указатель на обстоятельство, как во фразе: «Итак: всё плохо!». Только в случае с КП этот разделитель служит для указания типа (справа) для переменной (что слева).

2.2 Байтовый тип

Или просто байт. Обозначается ключевым словом BYTE. Переменная такого типа может принимать значения от 0 до 255. Это совсем не много, но для многих целей может оказаться вполне достаточно. Например, не существует минут и секунд более 60. Или например не бывает дня в месяце с номером 32. Пример описания переменной типа BYTE:

день   : BYTE;
уровень: BYTE;

Важно не забывать ставить точку с запятой после всех определений переменных (после определения последней переменной точку с запятой тоже нужно ставить). Кроме того, следует помнить, что особенности современных компьютеров: они не работают с одним байтом, они работают, скажем, сразу с 4-мя байтами. Поэтому возможны такие эффекты, как неэкономное расходование памяти. Как избежать таких эффектов будет рассмотрено в дальнейших частях.

2.3 Короткое целое

Короткое целое число в Компонентном Паскале определено как 2 байта. В редакции 1.7 сказано, что размеры типов не зависят от аппаратной платформы, но в текущей реализации Компонентного Паскаля, которая была скомпилирована под архитектуру 32 бита, короткое целое именно 2 байта. Диапазон чисел, которые умещаются в эти 2 байта составляет примерно от -32000 до +32000. Короткое целое обозначается ключевым словом SHORTINT.

Пример объявления коротких целых:

кцПачк_всего : SHORTINT; (*счётчик пачек *)
кцПалет_всего: SHORTINT; (*всего палет*)

Как видно, в целом, определение переменных базовых типов однообразно и их легко запомнить. Загадочные буквы впереди имён – это префиксы, для напоминания типа переменной программисту. Подставлять их совсем не обязательно, но автор рекомендует это делать.

2.4 Целое

Целое число является основным типом целых чисел для машин с 32 битами на машинное слово. Для Компонентного Паскаля это именно тот случай. Целое число занимает в памяти 4 байта. Такого количества памяти хватает на описание числа примерно от -2,1 млрд. до +2,1 млрд. Не часто встречаются числа с таким динамическим размахом. Целый тип описывается ключевым словом INTEGER:

цСчётчик1: INTEGER;
цСчётчик2: INTEGER;

И здесь ничего нет такого, чтобы потребовало особого способа описания переменных.

2.5 Длинное целое

Самый широкий диапазон целых чисел, который встроен в Компонентном Паскале. Занимает 8 байт, представляет целые числа в диапазоне примерно от -9,2×10¹⁸ до 9,2×10¹⁸. Даже сложно представить, где такие числа вообще могут потребоваться обычным людям. Обозначаются такие переменные как LONGINT:

дцСолнце_дист: LONGINT; (* расстояние до Солнца *)
дцПлутон_дист: LONGINT; (* расстояние до Плутона *)

Следует помнить, что сборка BlackBox Intron (впрочем, как и другие) оптимизированы под 32-х битную архитектуру, поэтому работа с такими числами будет существенно медленней, чем с типом INTEGER.

3. Вещественные числа

Вещественные (дробные, рациональные) числа называются так потому, что в окружающем мире редко встречаются «целые» объекты. Например, слоны. Они вроде все слоны. Но слонёнок по массе — это целый слон? Если нет, то как отразить его массу через целого слона? Кроме того, очень часто приемлемо записывать числа с заданной точностью. Они для этого подходят как никто. Таким образом, вещественные числа находят более чем широкое применение в промышленности.

3.1 Короткое вещественное

Такие числа соответствуют вещественным числам в языке Си. В памяти они занимают 4 байта, но в отличии от целых чисел они имеют особый формат при хранении. Это приводит к тому, что точность таких чисел ограничивается в 7-8 десятичных цифр. На зато диапазон этих чисел раздвигается до –3,4×10³⁸…–10^–38 в отрицательной области, и до 10^–38…3,4*10³⁸ в области положительных чисел. Даже по сравнению с типом LONGINT это оооочень много. Но есть и обратная сторона медали. Если в типе LONGINT точность до последнего знака, то в данном случае (как уже было выше упомянуто) только до 7-8. Поэтому, если в вычислениях важна точность, надо помнить о том, что точность больших чисел огрубляет точность малых чисел. Это правило определяет порядок работы с вещественными числами: «сначала маленькие, потом большие» при увеличении, и «сначала большие, потом маленькие» при уменьшении. Такие числа обозначаются ключевым словом SHORTREAL:

вЗил_масса  : SHORTREAL; (* масса автомобиля ЗиЛ *)
вКамаз_масса: SHORTREAL; (* масса автомобиля КамАЗ *)

Отдельно стоит упомянуть то, что вещественные числа обрабатываются на математическом сопроцессоре, и обычно, работа с вещественными числами происходит медленней, чем с целыми. 308). Точность составляет 15-17 десятичных знаков. Если через штуки записывать количество атомов во Вселенной — такой точности как раз должно хватить³⁾. Переменная вещественного типа описывается ключевым словом REAL:

двАндром_масса: REAL; (* масса галактики Андромеды *)
двГалак_масса : REAL; (* масса нашей галактики *)

4. Литерные типы

Литерными типами называют такие типы данных, которые имеют какое-либо отношение к отображению чего-либо. Например, буквы, строки, тексты, цифры, управляющие символы (перевод строки, новая строка, гудок и т.д.). Дело в том, что такие символы крайне важны для человека (и к ним совершенно равнодушен компьютер). Но на экране, принтере, плоттере — любой из этих символов состоит из множества точек (матрицы). И такая матрица может достигать размера 2400х4800 точек. Да ещё и они могут быть цветные (разных цветов все точки), и таким образом потребуется непомерное количество байтов для хранения всех возможных изображений литер и их цветов. И это ещё не говоря о всяких графических пиктограммах (смайлики, флажки, стрелки, дома и т. д.). Поэтому в своё время был предложен компромиссный вариант для хранения литер. Суть идеи состояла в том, что печатной (служебной) литере должен соответствовать свой код-число. А уж если потребуется, потом можно добавить различные способы вывода кода этой литеры на экран, принтер, плоттер и т. д. Тогда хранение литеры в памяти компьютера становится компактным и универсальным.

4.1 Литеры набора Latin-1

Эти литеры занимают в памяти ПК всего 1 байт. Если речь идёт исключительно о латинском алфавите (22 буквы), то им вполне можно пользоваться. Но вот проблема: если будет желание выводить символы на национальном алфавите, вместо ожидаемого результата будет непонятно что. А суть этой проблемы в том, что этот набор литер принимался как стандарт на заре компьютерной эпохи. Мало кто задумывался об этой проблеме, поэтому литеры набора Latin-1 даны скорее для обратной совместимости со старыми программами, чем для реального использования. Переменные такого типа описываются ключевым словом SHORTCHAR:

клЛат_а: SHORTCHAR; (* латинская литера "а" *)
клЛат_б: SHORTCHAR; (* латинская литера "б" *)

Стоит добавить, что кроме букв и цифр в литерах Latin-1 есть ещё и разные интересные значки, которые, иногда, могут и пригодиться ⁴⁾.

4.2 Литеры набора Unicode

Этот набор литер по сравнению с предыдущим является более прогрессивным. Он лишён недостатков Latin-1, но у каждой медали две стороны. Да, теперь в этот набор Unicode помещаются литеры всех языков мира существующих, или когда-либо существовавших. Туда же помещаются различного рода пиктограммы из всех сфер жизни (значки Солнца, Луны, Земли и даже «Серп и молот»). Но, если байтовые литеры было легко сравнивать, так как они располагались в алфавитном порядке, то как понять, какой код меньше и на каком основании: английская литера «а» или русская литера «а»? А это совершенно разные литеры. К счастью, все (или почти все) процедуры для работы с литерами Unicode написаны, и сомнительно, что программисту придётся писать что-то своё (с высокой степенью вероятности это будет велосипед, как говорят программисты). Такой тип переменных описывается ключевым словом CHAR:

лАнг_а: CHAR; (* английская литера "a" *)
лРус_а: CHAR; (* русская литера "а" *)

Ещё раз стоит обратить внимание — в данном примере (в наборе Unicode) русские и английские литеры кодируются различными кодами, хотя внешне и выглядят одинаково⁵⁾. Именно из-за того, что в Unicode буквы кодируются разной длиной, (и не только буквы, но и значки, пиктограммы, иероглифы) правильно говорить не буква, а литера.

5. Константы

Константой называется такая переменная, которую нельзя изменять в ходе выполнения программы. Преимущества констант перед переменными можно выразить следующими положениями:

1. Тип констант определяется автоматически. Т. е. программисту не нужно думать при описании константы о том, какой тип данных должен наилучшим образом соответствовать именно этой константе.

2. Преимущество констант перед переменными также в том, что если программист забудется, и попытается работать с константой, как с переменной — компилятор КП настойчиво напомнит программисту о том, что он сам запретил менять константу. И это приведёт к избежанию ошибок разработки и исполнения.

3. Также константы заметно быстрее обрабатываются компьютером, чем переменные.

Форма их определения существенно отличается от формы определения переменных:

_отказ = 1;
_добро = 2;
_хор   = 3;
_оч_хор = 4;
_вау   = 5;

Форма описания констант определена не через двоеточие, а через знак «равно». И в данном случае это вполне соответствует законам логики и математики. Также стоит обратить внимание, что константа _оч_хор и её знак «равно» не выровнены со всеми константами. Это допущение вполне приемлемо при оформлении кода. Ну что делать, если имя переменной, такое длинное? В данном примере все константы начинаются с символа подчёркивания. Такого требования нет в стиле по кодированию (code style), но авторы рекомендуют именно такой подход, чтобы было легче различать константы.

6. Преобразования типов

Язык Компонентный Паскаль был спроектирован, а не сочинён. Поэтому правила преобразования типов просты, понятны и предсказуемы.

6.1 Преобразования числовых типов

Как уже было выше описано, самым мощным диапазоном представления чисел является тип REAL. В случае преобразований при необходимости, этот тип преобразуется в более ограниченный — SHORTREAL(8 байт с плавающей запятой в 4 байта с плавающей запятой). Если этот тип придётся преобразовывать, он в свою очередь сужается до LONGINT (4 байта с плавающей запятой в 8 байта целочисленного значения). Тип длинное целое при сжатии переходит в тип INTEGER (8 байт в 4 байта). После типа целого сжатие диапазона идёт в сторону SHORTINT (2 байта). Короткое целое тоже может быть сжато до BYTE. Дальше диапазон числа уменьшить нельзя. Тип BOOLEAN, строго говоря числовым не является, хотя и содержит логические «0» и «1». Обратное преобразование также верно. Например, если разделить два целых числа 3 и 2 — результат будет вещественное число. КП прекрасно понимает, что без этого результат будет очень неточным. Поэтому, если результат такого деления попытаться присвоить целочисленной переменной — такой модуль даже не удастся скомпилировать — Компонентный Паскаль просто не позволит это сделать! В то же время, если сумма двух целых превышает динамический диапазон целого — КП на стадии компиляции постарается выяснить этот факт, и, по возможности, потребует результат присваивать длинному целому⁶⁾. Если выяснить на этапе компиляции это невозможно, КП во время исполнения остановит программу, и не позволит проскочить момент переполнения и «улететь программе в космос». Те же самые правила касаются и остальных преобразований типов. Коротко схему преобразования типов можно отобразить так:

REAL => SHORTREAL => LONGINT => INTEGER => SHORTINT => BYTE

Если нужно пройти в обратном направлении, то КП сначала попытается привести результат к более мощному типу, и если динамического диапазона обоих типов не хватает для хранения результата — КП потребует присвоения результата переменной, с заведомо более мощным типом. Отдельно следует отметить, что в КП – неявное приведение типов запрещено (такое приведение может привести к отрицательным побочным последствиям, типичный пример – Си).

6.2 Преобразования литерных типов

То, что выше было написано про числовые типы, применимо и к литерным типам. Также надо учитывать, что приведение SHORTCHAR к CHAR будет затруднено, так как КП просто не будет знать, какая была национальная кодировка типа SHORTCHAR. Коротко схему преобразования типов можно отобразить так:

CHAR => SHORTCHAR

7. Использование переменных и констант

В этом разделе будет приведён пример, показывающий как использовать переменные различных типов. Прежде чем будет приведён полный текст программы, кое-какие пояснения:

1. Описание переменных всегда в КП выносится в отдельную секцию модуля, которая обозначается ключевым словом VAR (variable, переменная).

2. Описание констант всегда в КП выносится в отдельную секцию модуля, которая обозначается ключевым словом CONST (constante, постоянная/неизменяемая).

Hello02.odc

MODULE КнигаПривет2;
	(* это вторая программа на языке
	Компонентный Паскаль. )TestHello02.Start

Необходимо обратить внимание, что константе _конст не нужно присваивать значение, а её тип (судя по всему) компилятор определил, как INTEGER. Наоборот, переменной цПерем необходимо присвоить значение, так как при запуске программы, в ней может находиться мусор (если это локальная переменная, но в нашем случае — глобальная — а значит, содержится 0). Мусор — это случайные значения, оставшиеся от работы предыдущей программы (которая пользовалась этим участком памяти). Переменной вПерем также не нужно присваивать начальное значение, так как нам оно — не интересно. Переменная вПерем получает своё значение в результате вычислений.

Если всё сделано правильно, то можно будет увидеть результат, примерно такой, как на врезке выше. Удивляемся размеру программы (88 байт), убеждаемся, что деление двух целых чисел привело к результату REAL, вспоминаем как вставить КОММАНДЕР и использовать его.

Кроме того, надо обратить внимание как на этот раз был выполнен импорт модуля Log — вместо его родного имени, теперь используется мЛог. По русски, с префиксом «м»(«модуль»), что делает код чуть более понятным. Этим полезным способом будем пользоваться и далее.

8. Немного о присваивании

В коде представленном выше используется знак равно в двух вариантах:

CONST
    _конст = 2;
.............<skip>...............
    цПерем  := 3;
    вПерем := c/i;

Здесь могут возникнуть вопросы, поэтому ниже приводятся необходимые пояснения:

1. В первом случае, при присвоении константе _конст значения 3 — стоит знак равно. И это правильная математическая форма записи.

2. Во втором случае, переменная вПерем содержит мусор, который никак не может быть равен _конст/цПерем (нет, конечно может, но вероятность такого совпадения асимптотически стремится к нулю), и чтобы подчеркнуть этот факт, что это не математическое уравнение, а инструкция присваивания в КП принято в инструкциях использовать символ :=, как не нарушающий математические соглашения.

3. Как видно из последней строки, выполнено неявное преобразование типов. Тип INTEGER приведён к типу REAL. Компонентный Паскаль соблюдает разумную необходимость с достаточностью в таких вопросах. Существует приличное число языков, где вообще не требуется выполнять явное приведение типов, или наоборот: на каждый чих необходимо вмешательство программиста. Едва ли оба подхода, как крайности — рациональны.

В ряде языков (в том числе, таком популярном, как Си) знак «равно» используется и для сравнения чисел в условиях, и это очень часто является источником ошибок. В Компонентном Паскале такие ситуации исключены. Ведь этот язык (в том числе) и для промышленного программирования.

Также необходимо обратить внимание, что может возникнуть соблазн, с целью ускорения исполнения программы приводить числа к более компактному виду, например REAL к SHORTREAL, полагая, что менее мощный тип обрабатывается быстрее. На самом деле, компилятор КП, как того требует программист, приведёт число к более компактному типу, для вычислений опять переведёт в более мощный тип, и чтобы согласовать результат вычислений с конечной переменной — ещё раз преобразует к более компактному виду. Таким образом, не только не будет прироста скорости вычислений, но и заметная её потеря. Основными типами чисел в КП являются INTEGER и REAL. Именно ими и стоит пользоваться. Все остальные базовые типы чисел нужны только для межмашинного обмена данными, либо экономии оперативной памяти.

9. Заключение

Эта глава довольна важна для понимания того, что базовые типы (или, как иногда говорят фундаментальные) не зря различаются на четыре группы. В природе их представления и обработки есть коренные отличия. Конечно, можно было обойтись одним-двумя базовыми типами, но на практике такое ограничение бывает неудобно. Раздувать число базовых типов тоже смысла не имеет — это лишь усложнит овладение языком и снизит надёжность программ.

blackbox/manual/var-const.txt · Последнее изменение: 2020/10/29 07:08 (внешнее изменение)

Числа: натуральные, целые, рациональные, иррациональные, действительные, комплексные

Тестирование онлайн

• Округление чисел

Натуральные числа

Это числа, которые используются при счете: 1, 2, 3… и т.д.

Ноль не является натуральным.

Натуральные числа принято обозначать символом N.

Целые числа. Положительные и отрицательные числа

Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «-«, называются отрицательными.

Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.

Рациональные числа

Это конечные дроби и бесконечные периодические дроби . Например,

Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.

Иррациональные числа

Бесконечная непериодическая дробь называется иррациональным числом. Например:

Множество иррациональных чисел обозначается J.

Действительные числа

Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.

Действительные числа обозначаются символом R.

Округление чисел

Рассмотрим число 8,759123… . Округлить до целой части означает записать лишь ту часть числа, которая находится до запятой. Округлить до десятых означает записать целую часть и после запятой одну цифру; округлить до сотых — после запятой две цифры; до тысячных — три цифры и т.д.

Округлить 8,759123… с точностью до целой части.

Округлить 8,759123… с точностью до десятой части.

Округлить 8,759123… с точностью до сотой части.

Округлить 8,759123… с точностью до тысячной части.

Типы данных в языке Си : целые, вещественные, символьные

 

Тип данных определяет множество значений, набор операций, которые можно применять к таким значениям и способ реализации хранения значений и выполнения операций.

Процесс проверки и накладывания ограничений на типы используемых данных называется контролем типов или типизацией программных данных. Различают следующие виды типизации:

• Статическая типизация — контроль типов осуществляется при компиляции.
• Динамическая типизация — контроль типов осуществляется во время выполнения.

Язык Си поддерживает статическую типизацию, и типы всех используемых в программе данных должны быть указаны перед ее компиляцией.

Различают простые, составные и прочие типы данных.

 

Простые данные

Простые данные можно разделить на

• целочисленные,
• вещественные,
• символьные
• логические.

 

Составные (сложные) данные

• Массив — индексированный набор элементов одного типа.
• Строковый тип — массив, хранящий строку символов.
• Структура — набор различных элементов (полей записи), хранимый как единое целое и предусматривающий доступ к отдельным полям структуры.

 

Другие типы данных

• Указатель — хранит адрес в памяти компьютера, указывающий на какую-либо информацию, как правило — указатель на переменную.

 
Программа, написанная на языке Си, оперирует с данными различных типов. Все данные имеют имя и тип. Обращение к данным в программе осуществляется по их именам (идентификаторам).

Идентификатор — это последовательность, содержащая не более 32 символов, среди которых могут быть любые буквы латинского алфавита a — z, A — Z, цифры 0 — 9 и знак подчеркивания (_). Первый символ идентификатора не должен быть цифрой.

Несмотря на то, что допускается имя, имеющее до 32 символов, определяющее значение имеют только первые 8 символов. Помимо имени, все данные имеют тип. Указание типа необходимо для того, чтобы было известно, сколько места в оперативной памяти будет занимать данный объект.

Компилятор языка Си придерживается строгого соответствия прописных и строчных букв в именах идентификаторов и лексем.

Верно	Неверно
int a = 2, b; b = a+3;	Int a=2;  // правильно int INT a=2;
	int a = 2, b; b = A + 3; // идентификатор А не объявлен
	int a = 2; b = a + 3; // идентификатор b не объявлен

Целочисленные данные

Целочисленные данные могут быть представлены в знаковой и беззнаковой форме.

Беззнаковые целые числа представляются в виде последовательности битов в диапазоне от 0 до 2ⁿ-1, где n-количество занимаемых битов.

Знаковые целые числа представляются в диапазоне -2^n-1…+2^n-1-1. При этом старший бит данного отводится под знак числа (0 соответствует положительному числу, 1 – отрицательному).

Основные типы и размеры целочисленных данных:

Количество бит	Беззнаковый тип	Знаковый тип
8	unsigned char 0…255	char -128…127
16	unsigned short 0…65535	short -32768…32767
32	unsigned int	int
64	unsigned long int	long int

Вещественные данные

Вещественный тип предназначен для представления действительных чисел. Вещественные числа представляются в разрядной сетке машины в нормированной форме.

Нормированная форма числа предполагает наличие одной значащей цифры (не 0) до разделения целой и дробной части. Такое представление умножается на основание системы счисления в соответствующей степени. Например, число 12345,678 в нормированной форме можно представить как

12345,678 = 1,2345678·10⁴

Число 0,009876 в нормированной форме можно представить как

0,009876 = 9,876·10^-3

В двоичной системе счисления значащий разряд, стоящий перед разделителем целой и дробной части, может быть равен  только 1. В случае если число нельзя представить в нормированной форме (например, число 0), значащий разряд перед разделителем целой и дробной части равен 0.

Значащие разряды числа, стоящие в нормированной форме после разделителя целой и дробной части, называются мантиссой числа.

В общем случае вещественное число в разрядной сетке вычислительной машины можно представить в виде 4 полей.

 
Различают три основных типа представления вещественных чисел в языке Си:

Тип	Обозна- чение в Си	Кол-во бит	Биты степени	Мантисса	Сдвиг
простое	float	32	30…23	22…0	127
двойной точности	double	64	62…52	51…0	1023
двойной расширен- ной точности	long double	80	78…64	62…0	16383

Как видно из таблицы, бит целое у типов float и double отсутствует. При этом диапазон представления вещественного числа состоит из двух диапазонов, расположенных симметрично относительно нуля. Например, диапазон представления чисел типа float можно представить в виде:

Пример: представить число -178,125 в 32-разрядной сетке (тип float).

Для представления числа в двоичной системе счисления преобразуем отдельно целую и дробную части:

178₁₀ = 10110010₂.

0,125₁₀ = 0,001₂.

Тогда

178,125₁₀ = 10110010,001₂=1,0110010001·2¹¹¹

Для преобразования в нормированную форму осуществляется сдвиг на 7 разрядов влево).

Для определения степени числа применяем сдвиг:

0111111+00000111 = 10000110.

Таким образом, число -178,125 представится в разрядной сетке как

 

Символьный тип

Символьный тип хранит код символа и используется для отображения символов в различных кодировках. Символьные данные задаются в кодах и по сути представляют собой целочисленные значения. Для хранения кодов символов в языке Си используется тип char.
Подробнее о кодировке символов

 

Логический тип

Логический тип применяется в логических операциях, используется при алгоритмических проверках условий и в циклах и имеет два значения:

• истина — true
• ложь — — false

В программе должно быть дано объявление всех используемых данных с указанием их имени и типа. Описание данных должно предшествовать их использованию в программе.

Пример объявления объектов

 
 

int n;    // Переменная n целого типа
double a; // Переменная a вещественного типа двойной точности

Назад: Язык Си

Представление целых и вещественных чисел в памяти ЭВМ — Студопедия.Нет

Структура памяти компьютера

Известно, вся информация, которая попадает в компьютер, преобразуется в последовательность электрических импульсов. Наличие импульса принято условно обозначать «1», а его отсутствие — 0. Такой способ кодирования информации называется двоичным или бинарным. Один двоичный символ получил название бит. (bit -от английского binary digit — «двоичная цифра»). Двоичное кодирование автоматически дает способ кодирования чисел в двоичной системе счисления.

Вся информация, вводимая в компьютер и возникающая в процессе его работы, хранится в памяти компьютера. Упрощенно память можно представить себе как страницу, состоящую из отдельных строк. Каждая такая строка называется ячейкой памяти и разделяется на разряды. Содержимым любого разряда может быть либо 0, либо 1. Таким образом, в любую ячейку памяти записывается некоторый набор из нулей и единиц, который называется машинным словом.

Все ячейки памяти пронумерованы. Номер ячейки называют ее адресом. Наличие у каждой ячейки адреса позволяет отличать ячейки друг от друга, а также обращаться к любой ячейке.

При считывании хранящегося в ячейке машинного слова содержимое ячейки не изменяется. А вот при записи в ячейку информации прежнее содержимое ячейки стирается.

Существуют два основных формата представления чисел в памяти компьютера. Формат представления числа – это способ отображения содержимого в ячейке памяти.

Для кодирования целых чисел используется формат с фиксированной запятой, для задания некоторого подмножества действительных (или вещественных) чисел так называемое представление числа в формате с плавающей точкой.

Представление целых неотрицательных чисел.

Все целые числа хранятся в памяти компьютера в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая «располагается» справа от младшего разряда (вне разрядной сетки).

Целые числа могут представляться в компьютере со знаком и без знака, т.е. храниться как отрицательными, так и положительными.

Целые числа без знака обычно занимают в памяти один, два или четыре байта и принимают в однобайтовом формате значения от 00000000 до 11111111 (в двоичной системе счисления), а, например, в двухбайтовом формате — от 00000000 00000000 до 11111111 11111111. Таким образом, множество целых, которые могут быть представлены в памяти компьютера, ограничено, Диапазон значений зависит от размера области памяти, используемой для размещения чисел.

Если для хранения целого неотрицательного числа отводится одна ячейка памяти длиной 8 битов, то, например, двоичное число 10010011₂ будет храниться в такой ячейке памяти следующим образом:

Минимальное число соответствует 8 нулям и, численно равно 0:

Максимальное же значение целого неотрицательного числа получается в том случае, когда во всех разрядах будут стоять единицы, что соответствует десятичному числу 255:

Таким образом, диапазон изменения целых неотрицательных чисел при хранении в однобайтовой ячейке памяти — от 0 до 255.

Чтобы получить внутреннее представление целого положительного числа N, хранящегося в k-разрядной ячейке памяти, необходимо:

1) перевести число N в двоичную систему счисления;

2) полученный результат дополнить слева незначащими нулями до k разрядов.

Получим, например внутреннее представление целого числа 1607 в 2-х байтовой ячейке. Для этого сначала переведем число в двоичную систему: 1607₁₀= 11001000111₂. Внутреннее представление этого числа в ячейке будет следующим:

0

0

0

0

0

1

1

0

0

1

0

0

0

1

1

1

Диапазон изменения целых неотрицательных чисел при хране­нии в двухбайтовой ячейке памяти — от 0 до 65535.

Представление целых чисел со знаком.

Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), при этом старший (крайний левый) разряд отводится под знак числа. Если число положительное, то в этот разряд записывается 0, если отрицательное, — то 1. Например, десятичное число 2356₁₀ будет представляться в двоичном виде как 100100110100₂, тогда в 16-разрядной сетке оно будет представлено следующим образом:

0

0

0

0

0

1

1

0

0

1

0

0

0

1

1

1

Представление положительных чисел с учетом знака называется прямым кодом числа.

Для представления отрицательных чисел используется так называемый дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения (как известно все математические операции в процессоре сводятся к сложению).

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде, хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа. Подробно операции над числами в машинных кодах будут рассмотрены при изучении других дисциплин.

Для хранения целых чисел используется также формат длинных целых со знаком. Для хранения таких чисел отводится 4 ячейки памяти (32 бита).

Достоинством представления чисел в формате с фиксированной запятой является простота и наглядность представления чисел, а недостатком — относительно небольшой диапазон представления величин.

Представление вещественных чисел.

Вещественные числа хранятся в памяти компьютера и обрабатываются процессором в формате с плавающей запятой.

В этом случае число А представляется в виде А=m • qⁿ, где:

m — мантисса числа;

q — основание системы счисления;

n — порядок числа.

Например, 123,45 = 0,12345 • 10³ (здесь m = 0,12345, n = 3, q = 10).

Представление числа в форме с плавающей точкой неоднозначно. Например, справедливы следующие равенства:

12,345 = 0,0012345 х 10⁴ = 1234,5 х 10^-2 = 0,12345 х 10²

Чаще всего в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в таком представлении должна удовлетворять условию: 0,lp < m < 1р. Иначе говоря, мантисса меньше 1 и первая значащая цифра — не ноль (р — основание системы счисления).

При таком представлении запятая будет расположена в мантиссе перед первой значащей цифрой, что при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивает запись максимального количества значащих цифр числа, то есть максимальную точность представления числа в компьютере. Такое, наиболее выгодное для компьютера, представление вещественных чисел и называется нормализованным.

Примеры нормализованного представления чисел:

753,15 = 0,75315 х 10³;

0,000034 = — 0,34x 10^-4

Число в формате с плавающей запятой занимает в памяти компьютера 4, 8, 6 или 10 байтов.). При этом отдельно выделяются разряды для хранения знака числа, знака порядка, порядка и самой мантиссы.

…

…

 

 

Рис. 1. Представление числа в формате с плавающей запятой

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.

Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего, отличного от нуля, числа до наибольшего числа, представимого в машине при заданном формате.

Посмотрим на примере числа 6,2510, как записываются числа в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка.

6,25₁₀=110,01₂=0,11001×2¹¹

31	30							23	22	21							2	1	0
0	0	0	0	…			1	1	1	1	0	0	1	0	…		0	0	0

Следует учитывать, что способ представления вещественного числа в ячейке зависит от архитектуры конкретной ЭВМ.

definition of Вещественное число and synonyms of Вещественное число (Russian)

Веще́ственное, или действи́тельное число ^[1] — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений ^[2].

Если натуральные числа возникли в процессе счета, рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.

Наглядно понятие вещественного числа можно представить себе при помощи числовой прямой. Если на прямой выбрать направление, начальную точку и единицу длины для измерения отрезков, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять некоторое, и притом только одно, вещественное число. Вследствие этого соответствия термин числовая прямая обычно употребляется в качестве синонима множества вещественных чисел.

Понятие вещественного числа прошло долгий путь становления. Ещё в Древней Греции в школе Пифагора, которая в основу всего ставила целые числа и их отношения, было открыто существование несоизмеримых величин (несоизмеримость стороны и диагонали квадрата), то есть в современной терминологии — чисел, не являющихся рациональными. Вслед за этим Евдоксом Книдским была предпринята попытка построить общую теорию числа, включавшую несоизмеримые величины. После этого, на протяжении более двух тысяч лет, никто не ощущал необходимости в точном определении понятия вещественного числа, несмотря на постепенное расширение этого понятия^[3]. Лишь во второй половине XIX века, когда развитие математического анализа потребовало перестройки его основ на новом, более высоком уровне строгости, в работах К. Вейерштрасса, Р. Дедекинда, Г. Кантора, Э. Гейне, Ш. Мере^[3] была создана строгая теория вещественных чисел.

С точки зрения современной математики, множество вещественных чисел — непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле.

Множество вещественных чисел имеет стандартное обозначение — R («полужирное R»), или (англ. blackboard bold «R») от лат. realis — действительный.

  История становления понятия вещественного числа

  Наивная теория вещественных чисел

Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения (пропорции, в современном понимании — рациональные числа). Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным числом^[4].

Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. Теория Евдокса дошла до нас в изложении Евклида («Начала», книга V). По существу, теория Евдокса — это геометрическая модель вещественных чисел. С современной точки зрения, число при таком подходе есть отношение двух однородных величин — например, исследуемой и единичного эталона. Следует, однако, подчеркнуть, что Евдокс остался верен прежней традиции — он не рассматривал такое отношение как число; из-за этого в «Началах» многие теоремы о свойствах чисел затем заново доказываются для величин. Классическая теория Дедекинда для построения вещественных чисел по своим принципам чрезвычайно похожа на изложение Евдокса. Однако модель Евдокса неполна во многих отношениях — например, она не содержит аксиомы непрерывности, нет общей теории арифметических операций для величин или их отношений и др.^[5]

Ситуация начала меняться в первые века н. э. Уже Диофант Александрийский, вопреки прежним традициям, рассматривает дроби так же, как и натуральные числа, а в IV книге своей «Арифметики» даже пишет об одном результате: «Число оказывается не рациональным»^[6]. После гибели античной науки на передний план выдвинулись индийские и исламские математики, для которых любой результат измерения или вычисления считался числом. Эти взгляды постепенно взяли верх и в средневековой Европе^[7], где поначалу разделяли рациональные и иррациональные (буквально: неразумные) числа (их называли также мнимыми, абсурдными, глухими и т. п.). Полное уравнение в правах иррациональных чисел связано с трудами Симона Стевина (конец XVI века), который провозгласил^[6]:

Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной законченностью.

Он же, с некоторыми оговорками, легализовал отрицательные числа, а также развил теорию и символику десятичных дробей, которые с этого момента начинают вытеснять неудобные шестидесятеричные.

Спустя столетие Ньютон в своей «Универсальной арифметике» (1707) даёт классическое определение (вещественного) числа как отношения результата измерения к единичному эталону^[8]:

Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой за единицу.

Долгое время это прикладное определение считалось достаточным, так что практически важные свойства вещественных чисел и функций не доказывались, а считались интуитивно очевидными (из геометрических или кинематических соображений). Например, считался самоочевидным тот факт, что непрерывная кривая, точки которой расположены по разные стороны от некоторой прямой, пересекает эту прямую. Строгое определение понятия непрерывности также отсутствовало^[9]. Как следствие, немало теорем содержали ошибки, нечёткие или чрезмерно широкие формулировки.

Даже после того, как Коши разработал достаточно строгий фундамент анализа, положение не изменилось, поскольку теории вещественных чисел, на которую обязан был опираться анализ, не существовало. Из-за этого Коши сделал немало ошибок, положившись на интуицию там, где она приводила к неверным выводам: например, он полагал, что сумма ряда из непрерывных функций всегда непрерывна.

  Создание строгой теории

Первую попытку заполнить пробел в основаниях математики сделал Бернард Больцано в своей статье «Чисто аналитическое доказательство теоремы, что между любыми двумя значениями, дающими результаты противоположного знака, лежит по меньшей мере один действительный корень уравнения» (1817). В этой пионерской работе ещё нет целостной системы вещественных чисел, но уже приводится современное определение непрерывности и показывается, что на этой основе теорема, упомянутая в заглавии, может быть строго доказана^[10]. В более поздней работе^[11] Больцано даёт набросок общей теории вещественных чисел, по идеям близкой к канторовской теории множеств^[12], но эта его работа осталась неопубликованной при жизни автора и увидела свет только в 1851 году. Взгляды Больцано значительно опередили своё время и не привлекли внимания математической общественности.

Современная теория вещественных чисел была построена во второй половине XIX века, в первую очередь трудами Вейерштрасса, Дедекинда и Кантора. Они предложили различные, но эквивалентные подходы к теории этой важнейшей математической структуры и окончательно отделили это понятие от геометрии и механики.

  Конструктивные способы определения вещественного числа

При конструктивном определении понятия вещественного числа, на основе известных математических объектов (например, множества рациональных чисел ), которые принимают заданными, строят новые объекты, которые, в определённом смысле, отражают наше интуитивное понимание о понятии вещественного числа. Существенным отличием между вещественными числами и этими построенными объектами является то, что первые, в отличие от вторых, понимаются нами лишь интуитивно и пока не являются строго определённым математическим понятием.

Эти объекты и объявляют вещественными числами. Для них вводят основные арифметические операции, определяют отношение порядка и доказывают их свойства.

Исторически первыми строгими определениями вещественного числа были именно конструктивные определения. В 1872 году были опубликованы одновременно три работы: теория фундаментальных последовательностей Кантора, теория Вейерштрасса (в современном варианте — теория бесконечных десятичных дробей) и теория сечений в области рациональных чисел Дедекинда^[3][13].

  Теория фундаментальных последовательностей Кантора

В данном подходе вещественное число рассматривается как предел последовательности рациональных чисел. Чтобы последовательность рациональных чисел сходилась, на неё накладывается условие Коши:

Смысл этого условия заключается в том, что члены последовательности, начиная с некоторого номера будут лежать сколь угодно близко друг от друга. Последовательности, удовлетворяющие условию Коши, называются фундаментальными.

Вещественное число, определяемое фундаментальной последовательностью рациональных чисел , обозначим .

Два вещественных числа

и ,

определённые соответственно фундаментальными последовательностями и , называются равными, если

Если даны два вещественных числа и , то их суммой и произведением называются числа, определённые соответственно суммой и произведением последовательностей и :

Отношение порядка на множестве вещественных чисел устанавливается посредством соглашения, в соответствии с которым число по определению больше числа , то есть , если

Способ построения множества вещественных чисел с помощью фундаментальных последовательностей рациональных чисел является частным случаем конструкции пополнения произвольного метрического пространства. Как и в общем случае, полученное в результате пополнения множество вещественных чисел само уже является полным, то есть содержит пределы всех фундаментальных последовательностей своих элементов.

  Теория бесконечных десятичных дробей

Вещественное число определяется как бесконечная десятичная дробь, то есть выражение вида

где  есть один из символов или , называемый знаком числа,  — целое неотрицательное число,  — последовательность десятичных знаков, то есть элементов числового множества .

Бесконечная десятичная дробь интерпретируется как такое число, которое на числовой прямой лежит между рациональными точками вида

и для всех

Сравнение вещественных чисел в форме бесконечных десятичных дробей производится поразрядно. Например, пусть даны два неотрицательных числа

Если , то ; если то . В случае равенства переходят к сравнению следующего разряда. И так далее. Если , то после конечного числа шагов встретится первый разряд , такой что . Если , то ; если то .

Однако, при этом следует учитывать, что число . Поэтому если запись одного из сравниваемых чисел, начиная с некоторого разряда, представляет собой периодическую десятичную дробь, у которой в периоде стоит 9, то её следует заменить на эквивалентную запись, с нулём в периоде.

Арифметические операции над бесконечными десятичными дробями определяются как непрерывное продолжение^[14] соответствующих операций над рациональными числами. Например, суммой вещественных чисел и называется вещественное число , удовлетворяющее следующему условию:

Аналогично определяет операция умножения бесконечных десятичных дробей.

  Теория сечений в области рациональных чисел

В подходе Дедекинда вещественные числа определяются с помощью сечений в множестве рациональных чисел.

Сечением в множестве рациональных чисел называется всякое разбиение совокупности всех рациональных чисел на два непустых класса — нижний и верхний , так что каждое число из нижнего класса строго меньше всякого числа из верхнего:

Если существует число , которое является максимальным в нижнем классе, либо минимальным в верхнем классе, то это число разделяет множества и : числа нижнего и верхнего классов лежат по разные стороны от . Говорят также, что рациональное число производит данное сечение множества рациональных чисел.

Если же в нижнем классе сечения нет максимального элемента, а в верхнем — минимального, то не существует никакого рационального числа, которое разделяло бы множества и . В этом случае по определению полагают, что данное сечение определяет некоторое иррациональное число , которое находится между нижним и верхним классами, и тем самым производит данное сечение. Иначе говоря, для всякого сечения, не производимого никаким рациональным числом, вводят новый объект — иррациональное число, которое по определению больше всякого числа из нижнего класса и меньше всякого числа из верхнего класса:

Объединение всех рациональных и всех иррациональных чисел называют множеством вещественных чисел, а его элементы — вещественными числами.

Арифметические операции над вещественными числами определяются как непрерывное продолжение соответствующих операций над рациональными числами. Например, суммой вещественных чисел и называется вещественное число , удовлетворяющее следующему условию:

  Аксиоматический подход

Построить множество вещественных чисел можно разными способами. В теории Кантора вещественные числа — классы эквивалентных фундаментальных последовательностей рациональных чисел, в теории Вейерштрасса — бесконечные десятичные дроби, в теории Дедекинда — сечения в области рациональных чисел. Во всех этих подходах в результате мы получаем некоторое множество объектов (вещественных чисел), обладающих определёнными свойствами: их можно складывать, умножать, сравнивать между собой. Более того, коль скоро установлены свойства этих объектов, мы можем больше не апеллировать к тем конкретным конструкциям, с помощью которых они были построены.

В математике важна не конкретная природа объектов, а лишь математические соотношения, существующие между ними.

Для человека, который исследует математическое понятие количество элементов, безразлично, о чём говорить — о трёх яблоках или о трёх камнях, и их съедобность или несъедобность значения не имеет. В процессе отвлечения от несущественных признаков, то есть абстрагирования (лат. abstractio — отвлечение), он приходит к тому общему, что есть у трёх яблок и трёх камней — количеству элементов. Так возникает абстрактное понятие натурального числа. С этой точки зрения три яблока и три камня — две конкретные реализации, модели абстрактного понятия «число три».

Точно так же классы фундаментальных последовательностей рациональных чисел, бесконечные десятичные дроби, сечения в области рациональных чисел являются лишь конкретными реализациями, моделями вещественного числа. А само понятие вещественного числа определяется существующими для него математическими соотношениями. Коль скоро они установлены, определено и понятие вещественного числа.

Здесь уместно привести знаменитое высказывание Д. Гильберта, основоположника системного аксиоматического метода в математике, который, имея в виду аксиоматизацию геометрии, как-то заметил:

Следует добиться того, чтобы с равным успехом можно было говорить вместо точек, прямых и плоскостей о столах, стульях и пивных кружках. Давид Гильберт[15]

  Аксиоматика вещественных чисел

Множество называется множеством вещественных чисел, а его элементы — вещественными числами, если выполнен следующий комплекс условий, называемый аксиоматикой вещественных чисел:

  Аксиомы поля

На множестве определено отображение (операция сложения)

сопоставляющее каждой упорядоченной паре элементов из некоторый элемент из того же множества , называемый суммой и ( эквивалентная запись элемента множества ).

Также, на множестве определено отображение (операция умножения)

сопоставляющее каждой упорядоченной паре элементов из некоторый элемент , называемый произведением и .

При этом имеют место следующие свойства.

Коммутативность сложения. Для любых

Ассоциативность сложения. Для любых

Существование нуля. Существует элемент , называемый нулём, такой, что для любого

Существование противоположного элемента. Для любого существует элемент , называемый противоположным к , такой, что

Коммутативность умножения. Для любых

Ассоциативность умножения. Для любых

Существование единицы. Существует элемент , называемый единицей, такой, что для любого

Существование обратного элемента. Для любого существует элемент , обозначаемый также и называемый обратным к , такой, что

Дистрибутивный закон умножения относительно сложения. Для любых

Нетривиальность поля. Единица и ноль — различные элементы :

  Аксиомы порядка

Между элементами определено отношение , то есть для любой упорядоченной пары элементов из установлено, выполняется соотношение или нет. При этом имеют место следующие свойства.

Рефлексивность. Для любого

Антисимметричность. Для любых

Транзитивность. Для любых

Линейная упорядоченность. Для любых

Связь сложения и порядка. Для любых

Связь умножения и порядка. Для любых

  Аксиомы непрерывности

Каковы бы ни были непустые множества и , такие что для любых двух элементов и выполняется неравенство , существует такое число , что для всех и имеет место соотношение

Этих аксиом достаточно чтобы строго вывести все известные свойства вещественных чисел^[16].

На языке современной алгебры аксиомы первой группы означают, что множество является полем. Аксиомы второй группы — что множество является линейно упорядоченным множеством ( — ), причём отношение порядка согласовано со структурой поля  — . Множества, удовлетворяющие аксиомам первой и второй группы, называются упорядоченными полями. Наконец, последняя группа, состоящая из одной аксиомы, утверждает, что множество вещественных чисел обладает свойством непрерывности, которое также называют полнотой. Резюмируя, можно дать эквивалентное определение множества вещественных чисел.

Определение. Множеством вещественных чисел называется непрерывное упорядоченное поле.

  Непротиворечивость и категоричность аксиоматики

  Другие системы аксиом вещественных чисел

Существуют и другие способы аксиоматизации вещественных чисел. Например, вместо аксиомы непрерывности можно использовать любое другое эквивалентное ей условие, или группу условий. Например, в системе аксиом, предложенной Гильбертом, аксиомы групп и , по существу, те же, что и в приведённые выше, а вместо аксиомы используются следующие два условия:

Аксиома Архимеда. Пусть ^[17] и . Тогда элемент можно повторить слагаемым столько раз, чтобы образовавшаяся в результате сумма превзошла :

Аксиома полноты (в смысле Гильберта). Систему невозможно расширить ни до какой системы , так чтобы при сохранении прежних соотношений между элементами , для выполнялись бы все аксиомы —, .

Таким образом, можно дать следующее эквивалентное определение:

Определение. Множество вещественных чисел есть максимальное архимедово упорядоченное поле

В качестве другого примера аксиоматизации вещественных чисел можно привести аксиоматику Тарского (англ.), состоящую всего из 8 аксиом.

  Свойства

  Связь с рациональными числами

Очевидно, что на числовой прямой рациональные числа располагаются вперемешку с вещественными, причём множество вещественных чисел в известном смысле «плотнее» множества рациональных. Возникает закономерный вопрос, насколько часто на числовой прямой попадаются рациональные и вещественные числа и можно ли одни числа приблизить другими. Ответ на этот вопрос дают три леммы, основанные, в основном, на аксиоме Архимеда.^[18]

Лемма 1. Для любого вещественного числа и любого наперёд взятого положительного рационального расстояния найдётся пара рациональных чисел, отстоящих друг от друга менее, чем на это расстояние, таких что вещественное число лежит на отрезке между этими рациональными числами.

Эта лемма говорит о том, что любое вещественное число можно с заданной точностью с двух сторон приблизить рациональными числами.

Лемма 2. Между любыми двумя различными вещественными числами содержится рациональное число.

Очевидным следствием из этой леммы является тот факт, что между любыми двумя несовпадающими вещественными числами содержится целое бесконечное множество рациональных. Кроме того, ещё более очевидно, что между любыми двумя различными рациональными числами содержится вещественное.

Лемма 3. Приближение вещественного числа рациональными, описанное в лемме 1, идентифицирует вещественное число единственным образом.

Эти леммы прежде всего говорят о том, что множество вещественных чисел не такое «плотное» по сравнению с множеством рациональных чисел, как может показаться. Особенно ярко это иллюстрирует лемма 2. Все три леммы активно используются для доказательства различных теорем, связанных с операциями сложения и умножения вещественных чисел.

  Теоретико-множественные свойства

Изначально вещественные числа были естественным обобщением рациональных, но у них впервые было обнаружено свойство несчётности, которое говорит о том, что множество вещественных чисел нельзя занумеровать, т. е. не существует биекции между множествами вещественных и натуральных чисел. Чтобы показать несчётность всего множества вещественных чисел, достаточно показать несчётность интервала .^[18]

Пусть все числа указанного промежутка уже занумерованы некоторым образом. Тогда их можно выписать в следующем виде:

Здесь  — -я цифра -ого числа. Очевидно, что все числа указанного вида действительно принадлежат рассматриваемому промежутку, если только в каждом числе не все цифры сразу являются нулями или девятками.

Далее предлагается рассмотреть следующее число:

Пусть каждая цифра этого числа удовлетворяет следующим трём свойствам:

Такое число действительно существует на указанном промежутке, так как оно является вещественным, не совпадает ни с нулём, ни с единицей, а десятичных цифр достаточно, чтобы третье свойство выполнялось. Кроме этого, интересно тем фактом, что оно не совпадает ни с одним из чисел , выписанных выше, ведь иначе -я цифра числа совпала бы с -ой цифрой числа . Пришли к противоречию, заключающемуся в том, что как бы числа рассматриваемого промежутка ни были занумерованы, всё равно найдётся число из этого же промежутка, которому не присвоен номер.^[18]

Это свидетельствует о том, что множество вещественных чисел не является счётным. Его мощность называется мощностью континуума.

  Обобщение вещественных чисел

Поле вещественных чисел постоянно служило в математике источником обобщений, причём в различных практически важных направлениях. Непосредственно к полю примыкают следующие варианты обобщённых числовых систем.

1. Комплексные числа. Особенно плодотворны в алгебре и анализе.
2. Интервальные числа. Используются преимущественно в теории приближённых вычислений и в теории вероятностей.
3. Нестандартный анализ, который добавляет к вещественным числам бесконечно малые и бесконечно большие числа (разных порядков).

  Прикладные применения

Математическая модель вещественных чисел повсеместно применяется в науке и технике для измерения непрерывно меняющихся величин. Однако это не главное её применение, потому что реально измеренные величины всегда имеют конечное число десятичных знаков, то есть являются рациональными числами. Основное назначение этой модели — служить базой для аналитических методов исследования. Огромный успех этих методов за последние три века показал, что модель вещественных чисел в большинстве случаев достаточно адекватно отражает структуру непрерывных физических величин.

Сказанное, конечно, не означает, что вещественная числовая прямая есть точный образ реальной непрерывной величины. Например, современной науке пока не известно, дискретны ли пространство и время или делимы неограниченно; однако даже во втором случае модель вещественных чисел для этих величин должна рассматриваться как приближённая, поскольку понятия точки пространства и момента времени представляют собой идеализации, не имеющие реального аналога. Этот фундаментальный вопрос широко обсуждается в науке, начиная с апорий Зенона. Приближённой эта модель является и в применении к величинам, которые в классической физике рассматривались как непрерывные, но в действительности оказались дискретными (квантуемыми).

  См. также

  Примечания

1. ↑ Названия вещественное число и действительное число равнозначны. Исторически в Московской математической школе использовали термин действительное число, а в Ленинградской — вещественное число. В качестве примера можно привести две классические работы:
   • Лузин, Н. Н. Теория функций действительного переменного. (Московская школа)
   • Натансон, И. П. Теория функций вещественной переменной. (Ленинградская школа)
   В современных университетских учебниках употребляются оба термина:
   • Зорич В. А. Математический анализ. (МГУ, мехмат) — действительное число
   • Ильин В. А., Позняк В. Г. Основы математического анализа. (МГУ, физфак) — вещественное число
   • Кудрявцев, Л. Д. Курс математического анализа. (МФТИ) — действительное число
   • Фихтенгольц, Г. М. Курс дифференциального и интегрального исчисления. (СПбГУ) — вещественное число
2. ↑ См. Кудрявцев Л. Д. Курс математического анализа. — Т. 1. — С. 35-36., а также Бурбаки Н. Очерки по истории математики. — С. 146.
3. ↑ ^{1 2 3} Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. — С. 287-289.
4. ↑ Бурбаки Н.. Архитектура математики. Очерки по истории математики. — С. 147.
5. ↑ История математики. — Т. I. — С. 96-101.
6. ↑ ^{1 2} Бурбаки Н.. Архитектура математики. Очерки по истории математики. — С. 150-151.
7. ↑ История математики. — Т. I. — С. 190-191, 304-305.
8. ↑ История математики. — Т. II. — С. 35.
9. ↑ Бурбаки Н.. Архитектура математики. Очерки по истории математики. — С. 154.
10. ↑ Хрестоматия по истории математики. Математический анализ. Теория вероятностей / Под ред. А. П. Юшкевича. — М.: Просвещение, 1977. — С. 171-178. — 224 с.
11. ↑ Бернард Больцано.Парадоксы бесконечного.
12. ↑ Рыхлик Карел. Теория вещественных чисел в рукописном наследии Больцано // ИМИ, 1958. № 11. С. 515—532.
13. ↑ Рыбников К. А. История математики. — Т. 2. — С. 196.
14. ↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида
15. ↑ Рид К. Гильберт. — С. 79.
16. ↑ См. Кудрявцев Л. Д. Курс математического анализа. — Т. 1.
17. ↑
18. ↑ ^{1 2 3} В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 44 — 45, 63 — 64. — 672 с. — ISBN 5-482-00445-7

  Литература

  Использованная литература

• Арнольд И. В. Теоретическая арифметика. — М.: УЧПЕДГИЗ, 1938.

• Бурбаки Н. Очерки по истории математики / пер. с франц. И. Г. Башмаковой под ред. К. А. Рыбникова. — М.: Издательство иностранной литературы, 1963.

• Гильберт Д. Основания геометрии = Grundlagen der Geometrie / пер. с 7-го немецкого издания И. С. Градштейна под ред. П. К. Рашевского. — М.-Л.: Государственное издательство технико-теоретической литературы, 1948.

• Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. — Пер. с франц. — М.: МИР, 1986. — 432 с.

• Зорич В. А. Математический анализ. Часть I. — 4-е изд., испр. — М.: МЦНМО, 2002. — XVI+664 с. — ISBN 5-94057-056-9

• Ильин В. А., Позняк Э. Г. Основы математического анализа: В 2-х ч. Часть I. — 7-е изд. — М.: ФИЗМАТЛИТ, 2005. — 648 с. — ISBN 5-9221-0536-1

• История математики с древнейших времен до начала XIX столетия. В трех томах / под ред. Юшкевича. — М.: НАУКА, 1970. — Т. 1.

• Кантор Г. Труды по теории множеств / под ред. А. Н. Колмогоров, Ф. А. Медведев, А. П. Юшкевич,. — М.: НАУКА, 1985. — (Классики науки).

• Кудрявцев Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — 704 с. — ISBN 5-7107-4119-1

• Рид К. Гильберт / пер. с англ. И. В. Долгачева под ред. Р. В. Гамкрелидзе. — М.: НАУКА, 1977.

• Рыбников К. А. История математики. — М.: Издательство Московского университета, 1963. — Т. 2.

• Тер-Крикоров А. М., Шабунин М. И. Курс математического анализа. — 3-е изд., исправл. — М.: ФИЗМАТЛИТ, 2001. — 672 с. — ISBN 5-9221-0008-4

• Фихтенгольц Г. М. Основы математического анализа. — 7-е изд. — М.: ФИЗМАТЛИТ, 2002. — Т. 1. — 416 с. — ISBN 5-9221-0196-X

  Рекомендуемая литература

Тем, кто интересуется историей становления понятия вещественного числа, можно порекомендовать следующие две книги:

• Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики.

Прекрасное подробное изложение теории построения вещественных чисел с помощью фундаментальных последовательностей, а также теории построения вещественных чисел с помощью сечений в области рациональных чисел можно найти в следующей:

Желающим познакомиться с оригинальным ходом мысли самого Р. Дедекинда можно порекомендовать ту самую брошюру, в которой в 1872 году Дедекинд изложил свою теорию вещественного числа. Эта книжка на сегодняшний день остаётся одним из самых лучших и доступных изложений предмета. Имеется русский перевод:

Также прекрасное изложение теории Дедекинда имеется в классическом учебнике

• Фихтенгольц, Г. М. Основы математического анализа. — 7-е изд. — М.: ФИЗМАТЛИТ, 2002. — Т. 1. — 416 с. — ISBN 5-9221-0196-X

Построение теории вещественного числа с помощью бесконечных десятичных дробей можно найти в книгах

• Тер-Крикоров А. М., Шабунин М. И. Курс математического анализа.

• Ильин В. А., Познак Э. Г. Основы математического анализа: В 2-х ч. Часть I.

Аксиоматическое изложение теории вещественного числа можно найти в книгах

• Кудрявцев, Л. Д. Курс математического анализа. — 5-е изд. — М.: Дрофа, 2003. — Т. 1. — 704 с. — ISBN 5-7107-4119-1

• Зорич, В. А. Математический анализ. Часть I. — Изд. 4-е, испр. — М.: «МЦНМО», 2002. — 657 с. — ISBN 5-94057-056-9

Сущность аксиоматического метода и его сравнение с конструктивным подходом изложены Д. Гильбертом на нескольких страницах в Дополнении VI. О понятии числа в следующем издании классической работы

• Гильберт Д. Основания геометрии = Grundlagen der Geometrie. — пер. с 7-го немецкого издания И. С. Градштейна под ред. П. К. Рашевского. — М.-Л.: Государственное издательство технико-теоретической литературы, 1948.

   

Разница между действительными и целыми числами Разница между

Математики разработали системы, позволяющие определить, чем одно число отличается от другого. Как и другие концепции, числовые категории пересекаются. Поскольку действительные числа включают в себя все рациональные числа, такие как целые числа, они имеют схожие характеристики, такие как использование целых чисел и отображение на числовой прямой. Следовательно, ключевое различие заключается в том, что действительные числа являются общей классификацией, а целые числа — это подмножество, которое характеризуется как целые числа, которые могут иметь отрицательные свойства.

Что такое действительные числа?

Действительные числа — это значения, которые вы можете найти на числовой прямой, которая обычно выражается в виде геометрической горизонтальной линии, где выбранная точка функционирует как «начало координат». Те, которые попадают на правую сторону, помечаются как положительные, а те, что слева, как отрицательные. Описание «реальное» было дано Рене Декартом, известным математиком и философом 17 века. В частности, он установил разницу между действительными корнями многочленов и их мнимыми корнями.

Действительные числа включают целые, целые, натуральные, рациональные и иррациональные числа:

Целые числа — это положительные числа, не имеющие дробных частей и десятичных знаков, поскольку они представляют собой целые объекты без фрагментов или частей.

Целые числа — это целые числа, включающие отрицательную сторону числовой прямой.

Натуральные числа, также известные как счетные числа, похожи на целые числа, но ноль не включается, так как ничто по существу не может считаться «0».

Что касается его происхождения, то древнегреческий математик Пифагор заявил, что все числа рациональны. Рациональные числа — это частные или дробные части двух целых чисел. Если p и q являются целыми числами, а q не эквивалентно нулю, p / q — рациональное число. Например, 3/5 — рациональное число, а 3/0 — нет.

Гиппас, ученик Пифагора, не соглашался с тем, что все числа были рациональными. С помощью геометрии он доказал, что некоторые числа иррациональны. Например, квадратный корень из двух, равный 1.41 нельзя выразить дробью; следовательно, это иррационально. К сожалению, последователи Пифагора не признали действительность рациональных чисел. Это привело к тому, что Гиппаса утонули в море, что в то время считалось наказанием богов.

Что такое целые числа?

От латинского слова «целое число», которое переводится как «целое» или «нетронутый», эти числа не имеют дробных или десятичных компонентов, как целые числа.Числа включают положительные натуральные числа или счетные числа и их отрицательные числа. Например, -3, -2, -1, 0, -1, 2, 3 — целые числа. Обычная иллюстрация — это числа через равные промежутки времени на бесконечной числовой линии с нулем, который не является ни положительным, ни отрицательным, в середине. Следовательно, положительных моментов больше, чем отрицательных.

Что касается его истории, следующие учетные записи прослеживают, как впервые были использованы целые числа:

• В 200 г. до н. Э. отрицательные числа впервые были представлены красными стержнями в Древнем Китае.
• Примерно в 630 году нашей эры отрицательные числа использовались для обозначения долга в Индии.
• Арбермут Холст, немецкий математик, ввел целые числа в 1563 году как систему сложения и умножения. Он разработал систему в ответ на рост числа кроликов и слонов, на которых он экспериментировал.

Ниже приведены характеристики целых чисел:

Числа в правой части числовой прямой являются положительными и часто представляют собой большее значение по сравнению с их отрицательными числами.

Числа в левой части числовой линии часто рассматриваются как меньшее стандартное значение их положительных аналогов.

В центре числовой прямой, ноль — это целое число, которое не является ни положительным, ни отрицательным.

Как и целые числа, целые числа не имеют десятичных знаков и дробей.

Разница между действительными и целыми числами

Область действия действительных и целых чисел

Действительные числа включают целые, рациональные, иррациональные, натуральные и целые числа.С другой стороны, область действия целых чисел в основном связана с целыми числами, которые могут быть отрицательными и положительными. Следовательно, действительные числа более общие.

Фракции

Действительные числа могут включать дроби, такие как рациональные и иррациональные числа. Однако дроби не могут быть целыми числами.

Свойство с наименьшей верхней оценкой

Вещественные числа обладают свойством наименьшей верхней границы, которое также известно как «полнота». Это означает, что линейный набор действительных чисел имеет подмножества с супремумом.Напротив, целые числа не обладают свойством наименьшей верхней границы.

Собственность Архимеда

Свойство Архимеда, заключающееся в предположении, что существует натуральное число, которое равно или больше любого действительного числа, может применяться к действительным числам. Напротив, свойство Архимеда нельзя применить к целым числам.

Поле

Вещественные числа — это своего рода поле, которое является важной алгебраической структурой, в которой определены арифметические процессы.Напротив, целые числа не рассматриваются как поле.

Счетный

Как набор, действительные числа не могут быть исчислены, а целые — счетными.

Обозначения действительных чисел и целых чисел

Действительные числа обозначаются буквой «R», а набор целых чисел — буквой «Z». Н. Бурбаки, группа французских математиков в 1930-х годах, определила «Z» от немецкого слова «Zahlen», что означает число или целые числа.

Происхождение слова для действительных и целых чисел

Вещественные числа обозначают действительные корни многочленов, а целые числа произошли от латинского слова «целое», поскольку они не включают десятичные дроби и дроби.

Реальные числа против целых

Сводка вещественных и целых чисел

• На числовой прямой могут отображаться как действительные, так и целые числа.
• Целые числа — это подмножество действительных чисел.
• Целые числа имеют отрицательные числа.
• Как набор, действительные числа имеют более широкую область применения по сравнению с целыми числами.
• В отличие от целых чисел, действительные числа могут включать дроби и десятичные знаки.
• Свойства наименьшего ограничения, Архимеда и поля обычно применимы к действительным числам, но не к целым числам.
• В отличие от действительных чисел, целые числа строго счетны.
• «R» обозначает действительные числа, а «Z» — целые числа.

Джин Браун — зарегистрированный психолог, лицензированный профессиональный преподаватель, а также внештатный академический и творческий писатель. Она преподавала курсы социальных наук как на уровне бакалавриата, так и на уровне магистратуры. Джин также была научным консультантом и членом группы в ряде презентаций статей по психологии и специальному образованию. Ее сертификаты включают TESOL (Тампа, Флорида), Сертификат практики психиатрических отделений и Маркер дипломных курсов.

Последние сообщения от gene Brown (посмотреть все)

вещественных чисел

Реальные числа — это просто числа вроде:

1

12,38

-0,8625

3 4

π (пи)

198

Фактически:

Практически любое число, которое вы можете придумать, является действительным числом

Реальные числа включают:

		Целые числа (например, 0, 1, 2, 3, 4 и т. Д.)
		Рациональные числа (например, 3/4, 0.125, 0,333 …, 1,1 и т. Д.)
		Иррациональные числа (например, π , √2 и т. Д.)

Действительные числа также могут быть положительными , отрицательными или нулевыми.

Итак … что НЕ является действительным числом?

Математики также играют с некоторыми специальными числами, которые не являются действительными числами.

Строка вещественных чисел

Линия вещественных чисел похожа на геометрическую линию.

На линии выбрана точка «начало координат» . Точки справа положительные, а точки слева отрицательные.

Расстояние выбирается равным «1», затем отмечаются целые числа: {1,2,3, …}, а также в отрицательном направлении: {…, — 3, −2, −1 }

Любая точка на линии является действительным числом:

• Цифры могут быть целыми (например, 7)
• или рациональный (например, 20/9)
• или иррационально (как π)

Но мы не найдем Бесконечности или Мнимого числа.

Почему они называются «настоящими» числами?

Потому что это не мнимые числа.

Реальные числа не имели названия до того, как были придуманы мнимые числа. Их назвали «Реальными», потому что они не были Воображаемыми. Вот настоящий ответ!

Реальный не означает, что они находятся в реальном мире

Это , а не , называемые «Реальными», потому что они показывают ценность чего-то настоящего .

В математике нам нравятся чистые числа, когда мы пишем 0.5 мы имеем ввиду ровно половину.

Но в реальном мире половина может быть не точным (попробуйте разрезать яблоко ровно пополам).

Представление действительных и целых чисел

Последнее обновление: , четверг, 16 октября 2008 г., 09:43, , автор: Jean-François Pillou.

Представление числа в компьютере

Представление (или кодирование) числа означает его выражение в двоичной форме.Представление чисел в компьютере необходимо для того, чтобы он мог хранить их и манипулировать ими. Однако проблема в том, что математическое число может быть бесконечным (сколь угодно большим), но представление числа в компьютере должно занимать заранее определенное количество бит. Ключ, таким образом, состоит в том, чтобы заранее определить количество битов и то, как их интерпретировать, чтобы они могли представить фигуру как можно более эффективно. По этой причине было бы глупо использовать 16 бит для кодирования символа (65536 возможностей), когда обычно используется менее 256 бит.

Представление натурального числа

Натуральное число — это целое положительное число или ноль. Выбор количества используемых битов зависит от диапазона используемых чисел. Чтобы закодировать натуральные числа от 0 до 255, все, что нужно, это 8 бит (байт), так как 2 ⁸ = 256. Вообще говоря, кодирование n битов может использоваться для представления натуральных чисел от 0 до 2 ⁿ -1.

Чтобы представить натуральное число, определив, сколько битов будет использоваться для его кодирования, расположите биты в двоичную ячейку, при этом каждый бит будет помещен в соответствии с его двоичным весом справа налево, затем «заполните» неиспользуемые биты нули.

Представление целого числа

Целое число — это целое число, которое может быть отрицательным. Следовательно, число должно быть закодировано таким образом, чтобы отличать его положительное или отрицательное значение, и соблюдать правила сложения. Уловка заключается в использовании метода кодирования под названием с дополнением до двоек .

• Положительное целое число или ноль будет представлено в двоичном формате (основание 2) как натуральное число, за исключением того, что бит с наибольшим весом (крайний левый бит) представляет знак плюс или минус.Таким образом, для положительного целого числа или нуля этот бит должен быть установлен в 0 (что соответствует знаку плюс, поскольку 1 — знак минус). Таким образом, если натуральное число закодировано с использованием 4 бит, наибольшее возможное число будет 0111 (или 7 в десятичном формате).
  Как правило, наибольшее положительное целое число, закодированное с использованием n битов, будет 2 ^n-1 -1 .
• Отрицательное целое число кодируется с использованием дополнения до двух.
  Принцип дополнения до двоек :
  Выберите отрицательное число.
  • Возьмем его абсолютное значение (его положительный эквивалент)
  • Представлен в базе 2 с использованием n-1 битов
  • Каждый бит переключается с его дополнением (т. Е. Все нули заменяются единицами и наоборот)
  • Добавить 1
  Обратите внимание, что при сложении числа и его дополнения до двоек результат будет 0

Давайте посмотрим, как это продемонстрировано на примере:
Мы хотим закодировать значение -5, используя 8 бит. Для этого:

• запишите 5 в двоичном формате: 00000101
• включите его в комплект: 11111010
• прибавить 1: 11111011
• 8-битное двоичное представление -5 — 11111011

Комментарии:
Самый высокий весовой бит равен 1, так что это действительно отрицательное число.
Если сложить 5 и -5 (00000101 и 11111011), получится 0 (с остатком 1).

Представление действительного числа

Цель состоит в том, чтобы представить число с десятичной запятой в двоичном формате (например, 101,01 , которое не читается сто одна точка ноль один , потому что это фактически двоичное число, то есть 5,25 в десятичном) используя форму 1.XXXXX … * 2 ⁿ (в нашем примере 1.0101 * 2 ² ). Стандарт IEEE 754 определяет, как кодировать действительное число.
Этот стандарт предлагает способ кодирования числа, используя 32 бита, и определяет три компонента:

• знак плюс / минус представлен одним битом, бит с наибольшим весом (крайний левый)
• экспонента кодируется с использованием 8 бит сразу после знака
• мантисса (биты после десятичной точки) с оставшимися 23 битами

Таким образом, кодировка имеет следующий вид:
seeeeeeeemmmmmmmmmmmmmmmmmmmmm

• s представляет бит знака.
• , каждый e представляет бит экспоненты
• каждые м представляет собой бит мантиссы

Однако есть некоторые ограничения для экспонент:

• экспонента 00000000 запрещена
• экспонента 11111111 запрещена Однако иногда они используются для сообщения об ошибках. Эта числовая конфигурация называется NaN , вместо не число.
• 127 (01111111) необходимо добавить к экспоненте, чтобы преобразовать десятичное число в действительное в двоичном формате. ⁹
• Добавляем 127 к экспоненте, которая равна 9, дает 136, или по основанию 2: 10001000
• Мантисса состоит из десятичной части 525,5 в нормализованном основании 2, что равно 0000011011.
• Поскольку мантисса должна занимать 23 бита, для ее завершения необходимо добавить нули:
  00000110110000000000000
• Таким образом, двоичное представление 525.5 в соответствии со стандартом IEEE 754:
  0 1000 1000 00000110110000000000000
  0100 0100 0000 0011 0110 0000 0000 0000 (4403600 в шестнадцатеричном формате)

Вот еще один пример, на этот раз с использованием отрицательного действительного числа:
Значение -0.625 подлежит кодированию.

• Бит s равен 1, так как 0,625 отрицателен.
• 0,625 записывается по основанию 2 следующим образом: 0,101
• Мы хотим записать его в виде 1.01 x 2-1
• Следовательно, показатель степени равен 1111110, так как 127-1 = 126 (или 1111110 в двоичной системе)
• Мантисса — 01000000000000000000000 (представлены только цифры после десятичной точки, так как все число всегда равно 1)
• Двоичное представление числа 0.625 согласно стандарту IEEE 754:
  1 1111 1110 01000000000000000000000
  1111 1111 0010 0000 0000 0000 0000 0000 (FF 20 00 00 в шестнадцатеричном формате)

Действительное число — Простая английская Википедия, бесплатная энциклопедия

Действительное число — рациональное или иррациональное число, которое может быть выражено с помощью десятичной дроби. Обычно, когда люди говорят «число», они обычно имеют в виду «действительное число». Официальный символ для действительных чисел — полужирный шрифт R или полужирный шрифт R {\ displaystyle \ mathbb {R}} на доске. ^{[1] [2] [3]}

Некоторые действительные числа называются положительными. Положительное число «больше нуля». Реальные числа можно рассматривать как бесконечно длинную линейку. Для нуля и каждого другого числа есть отметка в порядке их размера. В отличие от физической линейки, здесь есть числа ниже нуля. Эти числа называются отрицательными действительными числами. Отрицательные числа «меньше нуля». Они похожи на зеркальное отображение положительных чисел, за исключением того, что им даны знаки минус (-), так что они обозначаются иначе, чем положительные числа.

Действительных чисел бесконечно много, потому что не существует наименьшего или наибольшего действительного числа. Независимо от того, сколько реальных чисел считается, всегда есть еще те, которые нужно подсчитать. Между действительными числами нет пробелов, а это означает, что если взять два разных действительных числа, между ними всегда будет третье действительное число. Это всегда верно, независимо от того, насколько близки первые два числа.

Если положительное число добавляется к другому положительному числу, то это число увеличивается.Если к числу добавить ноль, который также является действительным числом, то это число не изменится. Если к другому числу добавляется отрицательное число, оно становится меньше.

Действительные числа неисчислимы, а это означает, что невозможно поместить все действительные числа в последовательность. Любая последовательность действительных чисел будет пропускать действительное число, даже если последовательность бесконечна. Это делает действительные числа особенными, потому что даже при том, что существует бесконечно много действительных чисел и бесконечно много целых чисел, реальных чисел «больше», чем целых.Это часто выражается, говоря, что целые числа равны счетным , а действительные числа — несчетным .

Некоторые более простые системы счисления находятся внутри вещественных чисел. Например, все рациональные и целые числа являются действительными числами. Существуют также более сложные системы счисления, чем действительные числа, например комплексные числа. ^[2] Каждое действительное число является комплексным числом, но не каждое комплексное число является действительным числом. Точно так же 3/7 — рациональное число, но не целое.

Существуют разные типы действительных чисел. Иногда не говорят сразу обо всех реальных числах. Иногда говорят только о специальных, меньших по размеру наборах. У этих наборов есть особые названия. Они есть:

• Натуральные числа : это действительные числа без десятичной дроби, размер которых больше нуля.
• Целые числа : это положительные действительные числа без десятичных знаков, а также ноль. Натуральные числа также являются целыми числами.
• Целые числа : это действительные числа без десятичных знаков.К ним относятся как положительные, так и отрицательные числа. Целые числа тоже целые.
• Рациональные числа : это действительные числа, которые можно записать как дроби целых чисел. Целые числа также являются рациональными числами.
• Трансцендентные числа не могут быть получены путем решения уравнения с целыми компонентами.
• Иррациональные числа : это действительные числа, которые нельзя записать как дробь целых чисел. Трансцендентные числа тоже иррациональны.

Число 0 ( ноль ) является особенным. Иногда это рассматривается как часть подмножества, а иногда — нет. Это элемент Identity для сложения, что означает, что добавление нуля не меняет исходное число. Для умножения единичный элемент равен 1.

Одно действительное число, которое не является рациональным, — это 2 {\ displaystyle {\ sqrt {2}}}. Это число иррационально. Если квадрат нарисован со сторонами, равными одной единице длины, то длина линии между его противоположными углами будет 2 {\ displaystyle {\ sqrt {2}}}.

1. ↑ «Сборник математических символов». Математическое хранилище . 2020-03-01. Проверено 11 августа 2020.
2. ↑ ^{2,0 2,1} «Действительное число | математика». Британская энциклопедия . Проверено 11 августа 2020.
3. ↑ Вайсштейн, Эрик В. «Настоящее число». mathworld.wolfram.com . Проверено 11 августа 2020.

Реальные числа и их действия

Определения

Набор объектов setAny.представляет собой набор объектов, обычно сгруппированных в фигурных скобках {}, где каждый объект называется объектом elementAn в наборе. Например, {красный, зеленый, синий} — это набор цветов. Подмножество — набор, состоящий из элементов, принадлежащих данному набору. — это набор, состоящий из элементов, принадлежащих данному набору. Например, {зеленый, синий} — это подмножество цвета, указанного выше. Набор без элементов называется пустым набором — подмножество без элементов, обозначаемое ∅ или {}. и имеет свое собственное специальное обозначение, {} или ∅.

Изучая математику, мы ориентируемся на специальные наборы чисел. Набор натуральных (или счетных) чисел Набор счетных чисел {1, 2, 3, 4, 5,…}., Обозначенный N , равен

Три точки (…) называются многоточием и указывают на то, что числа продолжаются неограниченно. Набор целых чисел Набор натуральных чисел в сочетании с нулем {0, 1, 2, 3, 4, 5,…}., Обозначаемый W, представляет собой набор натуральных чисел в сочетании с нулем.

Набор целых чисел Набор положительных и отрицательных целых чисел в сочетании с нулем {…, −3, −2, −1, 0, 1, 2, 3,…}., Обозначаемый Z , состоит как из положительных, так и отрицательных целые числа, а также ноль.

Обратите внимание, что наборы натуральных и целых чисел являются подмножествами набора целых чисел.

Рациональные числа Числа в форме ab, где a и b — целые числа, а b — ненулевое значение., обозначенные Q , определяются как любое число в форме ab, где a и b являются целыми числами, а b не равно нулю. Десятичные дроби, которые повторяются или заканчиваются, рациональны. Например,

Набор целых чисел — это подмножество набора рациональных чисел, потому что каждое целое число может быть выражено как отношение целого числа к 1. Другими словами, любое целое число может быть записано над 1 и может считаться рациональным числом. Например,

Иррациональные числа Числа, которые нельзя записать как отношение двух целых чисел.определяются как любое число, которое нельзя записать как отношение двух целых чисел. Неповторяющиеся десятичные дроби, которые не повторяются, иррациональны. Например,

Множество действительных чисел Множество всех рациональных и иррациональных чисел., Обозначенное как R , определяется как множество всех рациональных чисел в сочетании с множеством всех иррациональных чисел. Следовательно, все числа, определенные до сих пор, являются подмножествами множества действительных чисел. Таким образом,

Номерная строка

Линия вещественных чисел Линия, которая позволяет нам визуально представлять действительные числа, связывая их с точками на линии., или просто числовая линия, позволяет нам визуально отображать действительные числа, связывая их с уникальными точками на линии. Действительное число, связанное с точкой, называется координатой. Вещественное число, связанное с точкой на числовой прямой. Точка на действительной числовой прямой, которая связана с координатой, называется ее графической точкой на числовой прямой, связанной с координатой.

Чтобы построить числовую линию, нарисуйте горизонтальную линию со стрелками на обоих концах, чтобы указать, что она продолжается без границ.Затем выберите любую точку, представляющую число ноль; эта точка называется началом координат Точка на числовой прямой, которая представляет собой ноль.

Отметьте одинаковые длины по обе стороны от исходной точки и пометьте каждую отметку, чтобы определить масштаб. Положительные действительные числа лежат справа от начала координат, а отрицательные действительные числа — слева. Число ноль (0) не является ни положительным, ни отрицательным. Обычно каждая отметка представляет собой одну единицу.

Как показано ниже, шкала не всегда должна быть одной единицей.В первой числовой строке каждая отметка представляет две единицы. Во втором случае каждая отметка представляет 17.

График каждого действительного числа отображается в виде точки в соответствующей точке числовой линии. Частичный график набора целых чисел Z следует:

Пример 1: Изобразите следующий набор действительных чисел: {−1, −13, 0, 53}.

Решение: Изобразите числа на числовой строке со шкалой, где каждая отметка представляет 13 единиц.

Фортран Урок 3

Фортран Урок 3

В уроке 1 Fortran мы кратко рассмотрели типы переменных в Fortran. Чтобы избежать ошибок в арифметике на Фортране, вы должны внимательно следить за правилами работы с числами различных типов. В то время как Basic более мягок, позволяя некоторую гибкость в смешивании переменных и чисел разных типов, Fortran менее снисходителен и заставит вас платить за оплошности.В этом уроке мы более внимательно рассмотрим некоторые правила и условности, которые необходимо соблюдать.

Целые числа

Целое число в Фортране — целое число; он не может содержать запятые или десятичную точку. Примеры чисел, которые Фортран считает целыми числами: 12, -1311, 0, +43, 123456789.

Для положительных целых чисел знак плюс не является обязательным, но отрицательным целым числам должен предшествовать знак минус. Примеры чисел , а не , которые Фортран считает целыми числами:

22 547, 3., 4,0, -43,57.

Из-за десятичных знаков Fortran будет рассматривать 3. и 4.0 как реальных чисел.

Целое число N в GNU Fortran должно лежать в диапазоне

–2 147 483 648 ≤ N ≤ 2 147 483 647.

Одна особенность Фортрана заключается в том, что когда он выполняет арифметические действия с целыми числами, он настаивает на том, чтобы дать ответ, который также является целым числом. Если ответ на самом деле не является целым числом, Fortran делает его единым, отбрасывая десятичную точку и все цифры после нее.Например, Fortran утверждает, что

11/8 = 1, 15/4 = 3, -4/3 = -1, -50/6 = -8, 2/3 = 0.

Если вы хотите, чтобы Фортран выдал вам правильное значение 11/8, вы указываете ему вычислить 11/8, чтобы он интерпретировал числа как действительные числа и выдал правильное значение 1,375. Целочисленная арифметика в Фортране может привести к другим странным сюрпризам — например, распределительный закон деления недействителен, как показано в примере

(2 + 3) / 4 = 5/4 = 1, но (2/4) + (3 / 4) = 0 + 0 = 0.

Большинство встроенных функций в Fortran применяются к действительным числам, и попытки применить их к целым числам приводят к сообщениям об ошибках компилятора. Компилятор возразит, если вы попросите Фортран вычислить sqrt (5), но у него нет проблем с sqrt (5.). Аналогично, если вы объявите N целочисленной переменной и попросите Фортран вычислить sqrt (N), cos (N) или log (N), ваша программа не будет компилироваться, поскольку эти функции не могут работать с целыми числами. Один из способов решения этой проблемы — использовать промежуточную функцию

real (x),

который преобразует x в действительное число (если оно еще не равно единице).Тогда, например,

real (5) = 5., sqrt (real (5)) = sqrt (5.) = 2.23606801.

Компилятор не будет возражать, если N — целочисленная переменная, и вы попросите Фортран вычислить такую ​​композицию, как sqrt (real (N)) или cos (real (N)).

Если вы объявите, что A является целым числом, а затем сделаете присвоение A = 3,45, Fortran не будет жаловаться, но он усечет 3,45 и присвоит A значение A = 3. Аналогично, если вы вставите оператор A = sqrt (5.), Фортран усечет sqrt (5.) = 2.23606801 и сделайте вывод, что A = 2. Но таких ошибок легко избежать, если вы внимательно сделаете правильные операторы объявления типов для всех переменных в начале своей программы.

Действительные числа одинарной точности

Действительное число , или, точнее, действительное число одинарной точности , записывается Фортраном с десятичной точкой, даже если это целое число. Последовательность операторов

вещественное число x

целое число y

x = 3

y = 3

print *, «x =», x, «but y =», y , «- странно!»

производит вывод

x = 3.но y = 3 — странно!

GNU Fortran использует до 9 цифр, не считая десятичной точки, для представления действительных чисел. Он сообщит, что

sqrt (3.) = 1,73205078, sqrt (1100.) = 33,1662483, sqrt (2,25) = 1,5.

Фортран может также использовать научную нотацию для представления действительных чисел. Последовательность En, прикрепленная к концу числа, где n — целое число, означает, что число нужно умножить на 10 ⁿ . Вот несколько способов написания числа 12.345:

1.2345E1, .12345E2, .012345E3, 12.345E0, 12345E-3.

При работе с одинарной точностью бесполезно назначать более 9 или 10 ненулевых цифр для представления числа, поскольку Фортран изменит все последующие цифры на 0. (10-я цифра может повлиять на то, как Фортран выполняет усечение.) Присваивания

x = 123456789876543., x = 123456789800000., x = 1234567898E5

дают тот же результат, если x уже был объявлен действительным числом одинарной точности. Обратите внимание, что запятые не используются для представления чисел; как бы полезны они ни были для людей, компьютеры считают их ненужными.

Действительные числа двойной точности

Действительное число двойной точности в GNU Fortran может быть представлено до 17 цифр до того, как произойдет усечение. Числа двойной точности записываются в экспоненциальной нотации, но с D, узурпировавшим роль E. Некоторые различные способы записи числа 12,345 как вещественного числа двойной точности: 1,2345D1, .12345D2, .012345D3, 12.345D0, 12345D-3.

При присвоении значения переменной с двойной точностью вы должны использовать эту нотацию в научном формате D, иначе значение будет считываться только с одинарной точностью.Например, если A имеет двойную точность и вы хотите присвоить A значение 3,2, вы должны написать

A = 3,2D0

вместо просто A = 3,2. (Дополнительное объяснение см. В разделе Ошибки преобразования базы 2 ниже.)

Когда число вводится с клавиатуры в ответ на команду «read *», пользователю не нужно беспокоиться о типах или формате ввода. Предположим, например, что x имеет одинарную или двойную точность, и пользователь должен ввести значение x в ответ на команду «read *, x».Если пользователь вводит просто «3» (целочисленный формат), GNU Fortran изменит 3 на правильный формат (на 3., если x имеет одинарную точность, и на 3D0, если x имеет двойную точность) перед присвоением его x. Аналогично, если x имеет двойную точность, и пользователь вводит 3.1 (формат одинарной точности), Fortran преобразует 3.1 в 3.1D0, прежде чем присвоить его x. (Однако с помощью обычного оператора присваивания «x = 3.1» из программы число , а не , изменено на формат двойной точности перед присвоением x.)

Число x можно преобразовать в двойную точность с помощью функции

дБ (х).

Ошибки преобразования Base 2

В то время как люди с 10 пальцами выполняют арифметические операции с основанием 10, у компьютеров нет пальцев, но они выполняют арифметические операции с помощью переключателей и, следовательно, используют основание 2. Как мы знаем, некоторые числа имеют бесконечное десятичное представление по основанию 10, например 1/3 = .33333…, 2/7 = .285714285714….

Невозможно представить такие числа в базе 10 с конечным числом цифр без ошибки округления.Компьютеры имеют ту же проблему при работе с основанием 2. В общем, единственные числа, представимые конечным числом цифр в базе 2, можно записать в форме m / n, где m и n — целые числа, а n — целая степень двойки. Примеры:

6 (= 6/2 ⁰ ), 5/2, 3/8, 29/16, 537/256, -3/1024.

Когда мы просим компьютеры делать за нас арифметические операции, возникает неизбежный источник ошибок. Мы даем компьютеру числа с основанием 10, и компьютер должен изменить их все на основание 2.Для большинства чисел существует ошибка округления, так как компьютер может работать только с конечным числом цифр за раз, а большинство чисел не имеют конечного представления в базе 2. Если компьютер работает в Fortran одинарной точности, он работает примерно с 9 цифрами (основание 10), поэтому ошибка округления будет происходить примерно в 8-м или 9-м разряде с основанием 10. При двойной точности эта ошибка появляется намного позже, примерно в 16-м или 17-м разряде с основанием 10. Если арифметические операции, выполняемые компьютером, очень сложны, эти ошибки округления могут накапливаться друг над другом, пока общая ошибка в конечном результате не станет намного больше.После того, как компьютер выполнил свою работу с основанием 2, он преобразует все числа обратно в основание 10 и сообщает свои результаты.

Даже если компьютер не выполняет никаких арифметических операций, а просто распечатывает числа, ошибка преобразования по основанию 2 все равно появляется. Вот программа, иллюстрирующая это явление:

.1D0

демонстрация программы

real x

двойная точность y, z

x = 1.1

y = 1.1

print *, «x =», x, «, y =», y, «, z =», z

конец

Несколько удивительный результат при запуске этой программы в GNU Fortran:

x = 1.10000002, y = 1.10000002, z = 1.1.

Переменная x имеет одинарную точность, и ошибка округления преобразования по основанию 2 отображается в 9-м разряде. Хотя y имеет двойную точность, он имеет ту же ошибку округления, что и x, поскольку значение 1.1 присваивается y только в режиме одинарной точности.(Что происходит, так это то, что Fortran преобразует 1,1 в базу 2 перед , изменяя его на двойную точность и присваивая его y.) Поскольку z имеет двойную точность, и ему присваивается значение 1,1 в режиме двойной точности, ошибка округления возникает намного позже , далеко за пределами девяти цифр, в которых печатаются результаты. Таким образом, значение z печатается точно в том виде, в котором оно получено. Используя операторы write и , формат (см. Ниже), можно напечатать z, используя 17 цифр; если вы это сделаете, вы обнаружите, что Fortran сообщает z = 1.1000000000000001, где последняя ошибочная 1 отображается как 17-я цифра.

Ошибка округления по основанию 2 возникает в предыдущем примере, потому что 1,1 = 11/10, а 10 не является степенью 2. Если вы измените программу, заменив 1,1 на 1,125 = 9/8, ошибки округления не будет. потому что 8 = 2 ³ — это степень двойки, поэтому значения x, y и z будут печататься точно так, как назначено. (Попробуйте !!)

Арифметика смешанного типа

В общем, следует избегать арифметики в Фортране, которая смешивает числа разных типов, так как правила быстро забываются и легко допускаются ошибки.Если в какой-либо арифметической операции Фортрану предлагается объединить целое число с действительным, обычно он будет ждать, пока он не будет вынужден объединить два, а затем преобразует целое число в действительный режим. Вот некоторые расчеты, иллюстрирующие процесс, которому следует Фортран, и показывающие, почему вам следует держаться подальше от этой ерунды:

5. * (3/4) = 5. * 0 = 5. * 0. = 0.

(5. * 3) / 4 = (5. * 3.) / 4 = 15. / 4 = 15. / 4. = 3.75

5.+ 3/4 = 5. + 0 = 5. + 0. = 5.

5 + 3. / 4 = 5 + 3. / 4. = 5 + 0,75 = 5 + 0,75 = 5,75

Если x и y объявлены как переменные с двойной точностью, и вы хотите умножить x на число, например, 2.1, чтобы получить y, вы должны написать

y = 2.1D0 * x.

Запись только y = 2.1 * x сохранит одинарную точность, когда 2.1 преобразуется в базу 2, тем самым вводя большую ошибку округления по основанию 2 и сводя на нет ваши усилия с двойной точностью.Аналогичные замечания относятся и к другим арифметическим операциям. Ошибки такого рода легко допускать при работе с двойной точностью. Лучший способ избежать их — строго следовать этому общему правилу:

Не смешивайте числа разных типов в арифметике Фортрана !!

Экспоненты и корни

Мы уже указываем на исключение из приведенного выше правила — можно использовать целые числа в качестве показателей действительных чисел. Это потому, что, выступая в качестве показателя степени, целое число действует скорее как «счетчик умножений», чем как активный участник арифметики.Например, когда Фортран выполняет вычисление 1,2 ⁵ , он выполняет умножение 1,2 * 1,2 * 1,2 * 1,2 * 1,2,

а целое число 5 никогда не учитывается! Таким образом, хотя это может показаться так на первый взгляд, вычисление 1,2 ⁵ на самом деле не смешивает целое число с действительным числом в любой арифметической операции. То же самое можно сказать и об отрицательных целых числах как показателях. Вычисление 1,2 ^-5 включает в себя умножение пяти множителей 1,2, а затем взятие обратной величины результата, так что число -5 не используется в реальной арифметике.

С рациональными показателями нужно обращаться осторожно. Распространенная ошибка начинающих программистов на Фортране — написать что-то вроде 5 ** (2/3) и ожидать, что Фортран вычислит значение 5 ^2/3 . Но Fortran будет рассматривать 2 и 3 как целые числа и вычислить 2/3 = 0 и придет к выводу, что 5 ** (2/3) = 5 ** 0 = 1. Правильное выражение для вычисления 5 ^2/3 равно

5 . ** (2./3.),

при этом все числа рассматриваются как действительные числа.

Таким же образом вычисляются корни чисел.Чтобы вычислить корень седьмой степени из 3, вы должны использовать выражение

3. ** (1./7.).

Если N — целочисленная переменная, и вы хотите вычислить корень N-й вещественной переменной x, не пишите x ** (1 / N), поскольку Fortran интерпретирует 1 / N как 0, когда N> 1. Вместо этого напишите x ** (1./real (N)), так что 1 и N сначала преобразуются в действительные переменные.

Запись и форматирование заявлений

Так же, как в Basic мы используем команды TAB и PRINT USING для более точного управления выводом программы, в Fortran мы можем использовать команды write с операторами формата .Хотя это может быть сложно, наиболее часто используемые параметры довольно просты в использовании. Типичный оператор write iswrite (*, 20) x, y, z.

Знак «*» в круглых скобках указывает Fortran на запись на экран, а «20» относится к метке оператора формата для этой команды write . X, y и z — это переменные, которые нужно распечатать. Оператор формата для этой команды write может иметь формат

20 (3f10.4).

В скобках «3» означает, что будут напечатаны 3 объекта, «f» означает, что это будут вещественных чисел с плавающей запятой, вещественных чисел (не экспоненциальная запись), «10» означает, что для печати будут использоваться 10 знаков. (считая знак, десятичную точку и цифры), а «.4» означает 4 цифры после десятичной точки. Некоторые распечатки, отформатированные таким образом, имеют следующий вид:

12345.6789, -1234.5678, 10002.3400.

Буква «f» в данном контексте представляет собой кодовую букву формата ; Вот некоторые из наиболее часто используемых кодовых букв формата и их значение:

строка

f	действительное число, формат с плавающей запятой
e	действительное число одинарной точности, экспоненциальное представление
d	Действительное число двойной точности, экспоненциальное представление
i	целое число
a	текстовая строка (символ)
x	пробел
/	вертикальный пробел
t	индикатор табуляции

Строки (в кавычках) могут быть помещены в операторы формата, разделенные запятыми.Вот примеры операторов записи с соответствующими операторами формата; справа от каждого находится описание соответствующего вывода:

Печатается строка

write (*, 10) n, x, y 10 формат (i4,4x, f10.4,2x, f10.4)	целое число n, напечатанное с использованием 4 знаков, затем 4 пробела, затем действительные числа x и y напечатаны с двумя пробелами между ними по 10 мест в каждом и 4 десятичных знака
запись (*, 20) область Формат 20 («Площадь есть», f8.5)	в кавычках, затем строка область действительного числа печатается, используя 8 разрядов с 5 знаками после запятой
написать (*, 30) «Площадь есть», площадь 30 формат (a, f8.5)	тот же результат, что и сразу выше
запись (*, 40) x, y, z 40 формат (3d20.14)	3 числа двойной точности x, y, z печатные, каждая с резервированием 20 мест, с 14 знаками после запятой
написать (*, 50) ученик, балл 50 формат (a20,4x, i3)	студент, текстовая строка до 20 символов, печатается, затем 4 пробелы, затем оценка, целое число используя максимум 3 места
запись (*, 60) r, A 60 формат (t10, f4.2, /, t10, f6.2)	табуляции до 10-го столбца, реальные число r, переход к следующей строке, табуляция до столбец 10, печатает действительное число A

Вы можете использовать циклы с операторами формата для печати массивов; вот примеры:

do i = 1, 10 напишите (*, 70) a (i) конец сделать 70 формат (f5.2)	массив действительных чисел, индексируется от 1 до 10, печатается; каждая запись занимает 5 мест с 2 десятичных знака, печатается на отдельной линии
написать (*, 80) (a (i), i = 1, 10) 80 формат (f5.2)	тот же результат, что и сразу выше
написать (*, 90) (a (i), i = 1, 10) 90 формат (10f5.2)	тот же вывод, что и выше, за исключением того, что все записи печатаются в той же строке
do i = 1, 5 напишите (*, 7) (m (i, j), j = 1, 6) 7 & nbsp формат (6i3) конец делать	печатает двумерный массив 5 x 6 m целых чисел, с каждой записью целого числа м (i, j) занимая 3 места.Каждая строка матрицы отображается в отдельной строке.

Вот другие полезные вещи, которые нужно знать о форматировании:

1. Если вы не укажете формат, GNU Fortran будет печатать действительные числа с использованием примерно 9 цифр, даже если вы выполняете вычисления с двойной точностью. Если вы хотите печатать с двойной точностью, вы должны использовать операторы записи и форматирования. При использовании двойной точности максимально возможное количество цифр составляет 17.