Числовое кодирование
Совместить достоинства аналогового и цифрового кодирования позволяет так называемое числовое кодирование. Согласно этой схеме кодирования элементы информации записываются числами, значения которых пропорциональны величине зарегистрированного сигнала. Данные, образующие числовую запись, очень удобны для автоматической обработки средствами вычислительной техники.
Сохранение подобия необходимо для записи информации естественного происхождения, переносимой электромагнитными или упругими волнами. Это предопределяет применение числового кодирования для записи фотографической, звуковой и видеоинформации с целью обработки данных на компьютере.
Системы счисления
Вопросы, касающиеся
записи чисел и действий с ними, относятся
к арифметике.
Набор правил представления (изображения) и наименования чисел называется системой счисления.
Знаки, используемые для записи чисел, называют цифрами.
Если значение, описываемое цифрой, зависит от ее положения в записи числа, система счисления называется позиционной.
Положение цифры в записи числа в позиционной системе счисления называют разрядом.
Основным параметром,
характеризующим ту или иную систему
счисления, является её основание.
Основание позиционной системы счисления
— это множитель, который определяет
изменение значения, описываемого
цифрой, при переносе её в следующий по
старшинству разряд. Следующий по
старшинству разряд располагается слева
от данного. Основание системы счисления
совпадает с количеством разных цифр,
используемых в ней для записи чисел.
В математике и в быту общепринята позиционная десятичная система счисления. Единица старшего разряда (например, в числе 10) соответствует десяти единицам младшего разряда. Запись чисел производится при помощи десяти разных цифр: О, 1,2,3,4,5,6,7,8,9.
Для представления числовых данных в компьютере используется двоичная система счисления. Основание этой системы равно двум. Соответственно, для записи чисел в этой системе используются только два символа (цифры): 0 и 1.
Если в разряде числа содержится минимальное число, для которого в системе счисления определён символ, значение этого разряда называется пустым. Если в разряде числа содержится максимальное число, для которого в системе счисления определён символ, значение этого разряда называется

Если при записи информации использовано числовое кодирование, а запись полученных чисел выполнена в двоичной системе счисления, можно сделать следующие выводы.
Поскольку разряд числа, записанного в двоичной системе, всегда либо полон, либо пуст и, в отличие от других систем счисления, не имеет промежуточных состояний, можно утверждать, что неопределённость значения двоичного разряда теоретически является минимально возможной и равна 1/2. В любых иных системах счисления неопределённость значения разряда выше, поскольку в них возможны промежуточные состояния разряда.
Поскольку неопределённость состояния разряда двоичного числа теоретически является минимально возможной, можно утверждать, что в закрытой информационной системе (только в закрытой) количество информации, снимающее эту неопределённость, является минимально возможным регистрируемым количеством информации.

Поскольку при записи информации образуются данные, мы можем утверждать, что содержание двоичного разряда является минимальным количеством данных, которым может быть представлено минимальное количество информации при её записи. Из сказанного вытекает, что двоичный разряд можно считать:
а) минимальной единицей измерения количества данных;
б) минимальной единицей представления информации при записи.
Полезные особенности двоичного разряда были заслуженно отмечены. Он получил индивидуальное название — бит. Слово «бит» происходит от английского слова bit, которое, в свою очередь, является производным от словосочетания bynary digit, что на русский язык переводится как двоичная цифра.
Бит — это двоичный
разряд. Его информационным содержанием
является его состояние (полон/пуст). Допустимо также говорить, что бит
установлен/сброшен, включён/выключен.
Можно говорить и о его числовом значении
(1 или 0).
Допустимо также говорить, что бит
установлен/сброшен, включён/выключен.
Можно говорить и о его числовом значении
(1 или 0).
В вычислительной технике наиболее устоявшейся является единица, называемая байтом. Байт — это композиция из восьми взаимосвязанных битов.
Байт, в отличие от бита, может быть весьма разнообразным по информационному содержанию. Прежде всего, его информационным содержанием являются 256 различимых состояний (2 8 = 256). При кодировании положительных целых чисел информационным содержанием байта является число от 0 до 255. Но поскольку кодировать можно не только положительные числа, байт может выражать отрицательное число, символ алфавита, цвет точки, высоту звука и многое другое.
Обратите
особое внимание на то, что байт — это
не группа из восьми последовательных
битов, а именно композиция. Байт
имеет собственное информационное
содержание.
Байт — это технический термин, связанный с определённым уровнем развития техники. Байт не всегда считался восьмиразрядным. В прошлом существовали компьютеры, в которых данные представлялись семиразрядными и шестиразрядными байтами. В настоящее время представление о байте как о восьмибитовой композиции общепринято, и нет оснований предполагать, что оно может измениться в ближайшем будущем,
Производными
единицами измерения количества данных
являются: килобайт (Кбайт), мегабайт
(Мбайт), гигабайт (Гбайт), терабайт
(Тбайт) и другие. В математике и физике
принято считать, что приставка кило- перед
обозначением единицы измерения
обозначает более крупную единицу
измерения, отличающуюся от исходной в
тысячу раз (приставка мега —
в миллион раз). Однако в информатике
используется иной подход. Здесь
соответствие между основной единицей
измерения и производной устанавливается
через масштабный множитель, являющийся
степенью двойки. Так, например, 1
Кбайт = 210 байт, то есть, если быть точным, 1Кбайт
= 1024 байта. Как видите, отличие от
тысячи невелико (менее 3%), и для
инженерных задач полученная погрешность
вполне приемлема. Но при переходе к
более крупным производным единицам
точность начинает быстро падать, и это
явление приходится учитывать.
Так, например, 1
Кбайт = 210 байт, то есть, если быть точным, 1Кбайт
= 1024 байта. Как видите, отличие от
тысячи невелико (менее 3%), и для
инженерных задач полученная погрешность
вполне приемлема. Но при переходе к
более крупным производным единицам
точность начинает быстро падать, и это
явление приходится учитывать.
1 Кбайт = 2ю байт = 1024 байт
1 Мбайт = 220 байт = 1 048 576 байт
1 Гбайт = 230 байт = 1 073 741 824 байт
Кодирование числовой информации — Кодирование информации
Представление числовой информации с помощью систем счисленияДля записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Система счисления — это знаковая система, в которой числа записываются по определенным
правилам с помощью символов некоторого алфавита, называемых цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).
При записи чисел в римской системе
счисления применяется правило: каждый меньший знак, поставленный слева от
большего, вычитается из него, в остальных случаях знаки складываются. Например,
римское число IX обозначает 9 (-1 + 10), а XI обозначает 11 (10 + 1).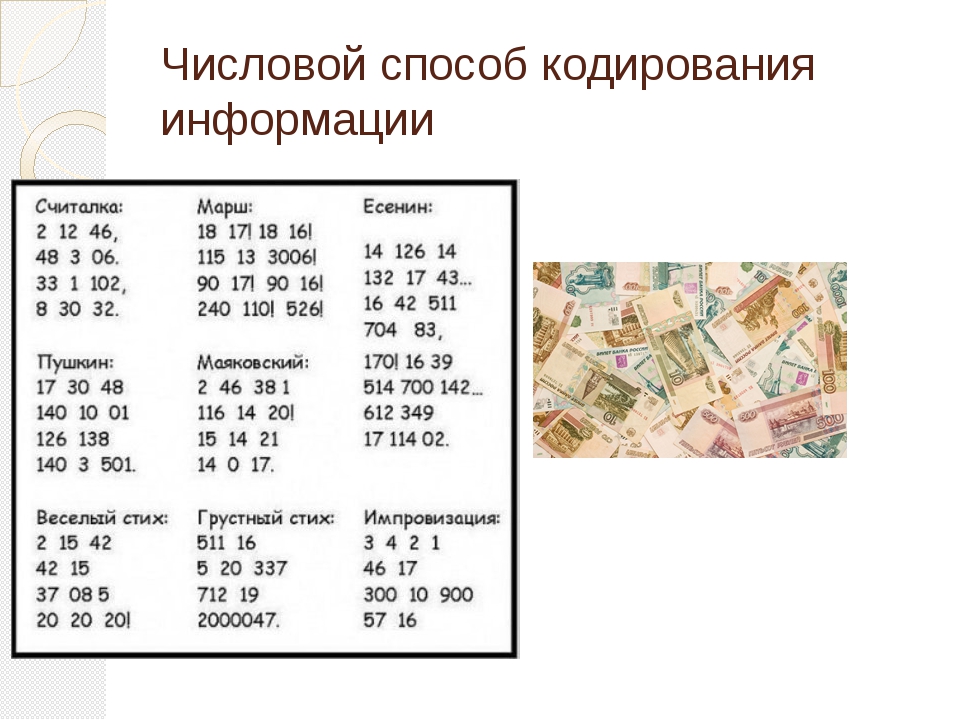
Позиционные системы счисления
Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
В настоящее время наиболее распространенными позиционными системами счисления являются десятичная и двоичная. Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Алфавит двоичной системы — две цифры {0, 1} (Табл.1).
Таблица 1.
| |||||||||
Десятичная система счисления. В
десятичной системе счисления цифра в крайней справа позиции обозначает единицы,
цифра, смещенная на одну позицию влево, обозначает десятки, еще левее — сотни,
затем тысячи и т. д. Рассмотрим в качестве примера десятичное число 555. Цифра
5 встречается в числе трижды, причем самая правая обозначает пять единиц,
вторая справа — пять десятков и, наконец, третья — пять сотен.
Выше десятичное число 555 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10, которое является основанием десятичной системы счисления.
В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:
55510 = 5*102 + 5*101 + 5*100.
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записываться следующим образом:
555,5510 = 5*102 + 5*101 + 5*100 + 5*10-1 + 5*10-2.
Число в позиционной системе счисления
записывается в виде суммы числового ряда степеней основания, в качестве
коэффициентов которых выступают цифры данного числа.
Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:
555,5510 *10 = 5555,510,
555,5510 : 10 = 55,55510.
Двоичная система счисления. Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, развернутая запись двоичного числа выглядит следующим образом:
А2 = 1*22 + 0* 21 + 1*20 + 0*2-1 + 1*2-2.
Это же число в свернутой форме:
А2 = 101,012.
Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево.
Например:
101,012 * 2 = 1010,12,
101,012 : 2 = 10,1012.
Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, т. е. в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут).
В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и т. д.
В информатике широко используются восьмеричная и шестнадцатеричная системы счисления. В восьмеричной системе основание равно 8 и алфавит состоит из восьми цифр {0, 1, 2, 3, 4, 5, 6, 7}. Запишем восьмеричное число 77 в свернутой и развернутой формах и переведем его в десятичную систему счисления:
778 = 7* 81 + 7 *80 = 6310.
В шестнадцатеричной системе основание
равно 16 и алфавит состоит из шестнадцати цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
А, В, С, D, E, F}, причем первые десять цифр имеют общепринятое обозначение, а
для записи остальных цифр {10, 11, 12, 13, 14, 15} используются первые шесть
букв латинского алфавита. Запишем шестнадцатеричное число в свернутой и
развернутой формах и переведем его в десятичную систему счисления:
Запишем шестнадцатеричное число в свернутой и
развернутой формах и переведем его в десятичную систему счисления:
ABCDEF16 = А*165 + В*164 + C*163 + D*162 + Е*161 + F*160 = 10*165 + 11*164 + 12*163 + 13*162 + 14*161 + 15*160 = 1125937510.
Перевод чисел в позиционных системах счисленияЧеловек использует десятичную систему счисления, а компьютер — двоичную систему счисления. Поэтому часто возникает необходимость перевода чисел из десятичной системы в двоичную и наоборот.
Перевод чисел из двоичной системы счисления в десятичную систему счисления. Преобразование чисел из двоичной системы счисления в десятичную выполнить довольно легко. Для этого необходимо записать двоичное число в развернутой форме и вычислить его значение.
Возьмем
любое двоичное число, например 10,112. Запишем его в развернутой
форме и произведем вычисления:
Запишем его в развернутой
форме и произведем вычисления:
10,112 = 1*21 + 0*20 + 1*2-1 + 1*2-2 = 1*2 + 0 *1 + 1 *1/2 + 1*1/4 = 2,7510.
Перевод целых чисел из десятичной системы счисления в двоичную систему счисления. Алгоритм перевода целого десятичного числа в двоичное следующий:
1) последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы счисления (на 2) до тех пор, пока частное от деления не окажется равным нулю;
2) получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности.
В качестве примера рассмотрим перевод десятичного числа 1910 в двоичную систему счисления, записывая результаты в таблицу (Табл.2).
Таблица 2. Перевод целого числа из десятичной системы счисления в двоичнуюВ результате получаем двоичное число:
А2 =
100112.
Перевод десятичных дробей в двоичную систему счисления. Алгоритм перевода десятичной дроби в двоичную следующий:
1) последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы (на 2) до тех пор, пока не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений;
2) получить искомую двоичную дробь, записав полученные целые части произведений в прямой последовательности.
В качестве примера рассмотрим перевод десятичной дроби 0,7510 в двоичную систему, записывая результаты в таблицу (Табл. 3).
Таблица 3. Перевод дробного числа из десятичной системы счисления в двоичную.
В результате получаем двоичную дробь:
А2 = 0,112.
Перевод чисел, содержащих и целую, и дробную часть,
производится в два этапа. Отдельно переводится по соответствующему алгоритму
целая часть и отдельно — дробная. В итоговой записи полученного числа целая
часть от дробной отделяется запятой.
Арифметические операции во всех позицинных системах счисления выполняются по одним и тем же хорошо известным вам правилам.
Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:
0 + 0 = 0
0 + 1 = 1,
1 + 0 = 1,
1 + 1 = 10.
Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания системы счисления, для двоичной системы счисления — большей или равной 2.
Сложение многоразрядных двоичных чисел происходит в
соответствии с вышеприведенной таблицей сложения с учетом возможных переносов
из младших разрядов в старшие. В качестве примера сложим в столбик двоичные
числа 1102 и 112 (Рис. 1).
1).
Рис.1.
Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим.
1102 = 1*22 + 1*21 + 0*20 = 610
112 = 1*21 + 1*20 = 310
610 + 310 = 910
Теперь переведем результат двоичного сложения в десятичное число:
10012 = 1*23 + 0*22 + 0*21 + 1*20 = 910
Сравнение результатов показывает, что сложение выполнено правильно.
Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой (Рис.2).
Рис.2.
Вычитание
многоразрядных двоичных чисел происходит в соответствии с вышеприведенной
таблицей вычитания с учетом возможных заемов из старших разрядов. В качестве
примера произведем вычитание двоичных чисел 1102 и 112 (Рис.3).
В качестве
примера произведем вычитание двоичных чисел 1102 и 112 (Рис.3).
Рис.3.
Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел:
Рис. 4.
Умножение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя. В качестве примера произведем умножение двоичных чисел 1102 и 112 (Рис.5).
Рис.5.
Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 1102 на 112 (Рис.6)
Рис.6.
Для проведения арифметических операций над числами,
выраженными в различных системах счисления, необходимо предварительно перевести
их в одну и ту же систему.
Числа в компьютере хранятся и обрабатываются в двоичной системе счисления. Оперативная память компьютера состоит из ячеек, в каждой из которых может храниться 8 битов информации, т. е. 8 разрядов двоичного числа.
Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, т. е. вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А2 = 111100002 будет храниться в ячейке памяти следующим образом:
Рис. 7.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целого неотрицательного числа. Минимальное число записывается в восьми разрядах памяти восемью нулями и равно 0. Максимальное число записывается восемью единицами и равно:
А = 1*27 +1*26 +1*25 + 1*24 + 1*23 + 1*22 + 1*21 + 1*20 = 1*28 — 1 = 25510.
Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.
Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное, записывается 1).
Например, отрицательное число -200210 = 111110100102 будет представлено в 16-разрядном представлении следующим образом:
Рис. 8.
Максимальное положительное число (с учетом выделения одного разряда на знак) для данного формата представления равно:
А = 215 — 1 = 32 76710.
Достоинствами представления чисел в формате с фиксированной
запятой являются простота и наглядность представления чисел, а также простота
алгоритмов реализации арифметических операций. Недостатком является небольшой
диапазон представления величин, недостаточный для решения математических,
физических, экономических и других задач, в которых используются как очень
малые дробные, так и очень большие числа.
Для представления чисел в диапазоне от очень маленьких дробей до очень больших чисел с высокой точностью используется формат с плавающей запятой. В этом случае положение запятой в записи числа может изменяться. Число в форме с плавающей запятой занимает в памяти компьютера 4 байта (число обычной точности) или 8 байтов (число двойной точности).
Кодирование числовой информации — Итформатика825Петрова
Как представляется информация
Издавна люди пользовались шифрами. Самыми простыми и удобными являются цифровые шифры.
Для обработки компьютером любая информация представляется в виде чисел, записанных с помощью цифр. Цифры представляются электрическими сигналами, с которыми работает компьютер. Для удобства различения в компьютере используются сигналы двух уровней. Один из них соответствует цифре 1, другой — цифре 0. Цифры 0 и 1 называются двоичными. Они являются символами, из которых состоит язык, понимаемый и используемый компьютером. 4=10000,…). Число 10 является основанием этой системы счисления.
4=10000,…). Число 10 является основанием этой системы счисления.
Действительно, если число меньше 10, то записывается соответствующая ему одна цифра.
Если число больше либо равно 10, но меньше 100, то оно представляется двумя цифрами: первая указывает количество полных десятков, содержащихся в числе, вторая — количество единиц в последнем неполном десятке.
Индекс внизу указывает систему счисления, в которой записано исходное число. Если число больше либо равно 100, но меньше 1000, то для его записи используется уже три цифры. Первая цифра — это количество полных сотен, содержащихся в числе, вторая цифра — количество полных десятков в последней неполной сотне, третья цифра — количество единиц в последнем неполном десятке.
При таком подходе для представления числа, большего либо равного 1000, но меньшего 10000, требуется уже четыре цифры. Первая цифра — количество полных тысяч, вторая — количество полных сотен, третья — количество полных десятков и четвертая — количество единиц.
Количество цифр, используемых для десятичного представления числа, на единицу больше, чем показатель наибольшей степени 10, содержащейся в числе. Это связано с тем, что в представлении участвует нулевая степень числа 10.
Таким образом, любое целое неотрицательное число в десятичной системе счисления представляется в виде:
где каждый из коэффициентов an, an-1,•••, a1, a0 является одной из цифр от 0 до 9, называемых десятичными цифрами, причем an не равно 0.
Общее количество цифр в десятичной записи числа равно количеству коэффициентов в представлении (1), т.е. n+1, где п — показатель наибольшей степени числа 10, содержащейся в исходном числе.
Например:
Коэффициенты в представлении (1) должны принимать значения от 0 до 9, причет коэффициент аn не должен быть равен нулю (ноль не может быть первой цифрой числа).
Двоичная система счисления
Двоичная система счисления — это система, в которой для записи чисел используются две цифры 0 и 1. n
n
Используя эту таблицу, можно записать:
В общем виде представление целого неотрицательного числа с помощью степеней двойки записывается так же, как и представление (1) с заменой числа 10 на число 2:
Здесь каждый из коэффициентов аn, an-1 ,•••,a1, a0 является одной из двух двоичных цифр 0 или 1, причем an=1.
Запись числа в двоичной системе строится так же, как и в десятичной: первой записывается цифра ап, второй — цифра ап-1 и т.д.,
последней — цифра а0.
Двоичный код числа — запись этого числа в двоичной системе счисления.
Таким образом, двоичным кодом числа является последовательность коэффициентов ап an-1 ••• a1 a0 из представления (2).
Коэффициенты в представлении (2) должны принимать только одно из двух значений: 0 или 1. Это обеспечивает однозначность такого представления.
Это обеспечивает однозначность такого представления.
Если какой-либо из коэффициентов больше 1, то происходит переход к следующей степени числа 2.
Например:
Старший коэффициент аn всегда равен 1, т.е. двоичный код всегда начинается с 1. Чтобы лучше понимать, как получается двоичный код некоторого числа, представим себе последовательность разрядов, каждый из которых может содержать только одну из двоичных цифр 0 или 1, т.е. один бит информации. В дальнейшем под битом и разрядом будем понимать одно и то же.
Посмотрим, как получается двоичное представление, например, числа 25. Число 25 представляется в виде суммы чисел из этой строки: 25=16+8+1. Каждое число берется только один раз — это обеспечивает однозначность двоичного кода. Затем выбранные числа заменяются равными им степенями двойки из верхней строчки таблицы: 16=24, 8=23, 1=20; 25=24+23+20. И, наконец, разряды, номера которых равны числам, выбранным из первой строчки таблицы заполняются единицами, а остальные — нулями.
Сколько чисел можно записать с помощью n битов
Уже описано, как получать двоичный код любого десятичного числа, т.е. переводить его из десятичной системы в двоичную. Рассмотрим теперь обратное действие: перевод числа из двоичной системы счисления в десятичную.
Итак, требуется найти десятичное число по известному двоичному коду этого числа. Воспользуемся представлением вида (2). Коэффициенты аn, an-l ,•••,a1, a0 известны. Значит, нужно вычислить значение выражения (2). Рассмотрим примеры. Пусть задан двоичный код 11012. Самый левый — старший бит — имеет номер 3. Следовательно, первое слагаемое равно 1•23. Следующий бит имеет
номер 2. Второе слагаемое равно 1•22. Третье слагаемое равно 0•21 четвертое слагаемое равно 1•20. Искомое число есть сумма четырех слагаемых: 1•23+1•22+0•21+1•20=8+4+1=13. Таким образом, 11012=13.
В десятичной системе следующее число получается из предыдущего путем прибавления единицы к количеству единиц предыдущего числа.
То же самое происходит при получении двоичного кода следующего числа из двоичного кода предыдущего: к младшему разряду двоичного кода предыдущего числа прибавляется единица.
Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, происходит перенос единицы в следующий слева разряд. Таким образом, правила сложения в двоичной системе таковы:
Наибольшее десятичное число, использующее для записи своего двоичного кода три бита, получается, когда значения всех трех битов равны единице.
Понятно, что наибольшее число, использующее для своей двоичной записи а битов, равно 2n -1. Следующее за ним число 2n требует для своей записи n+1 бит. Таким образом, используя п битов, можно записывать двоичные коды чисел от 0 до 2n -1, всего 2n чисел.
Как измеряется количество информации в компьютере
В информатике принято рассматривать последовательности битов длиной 8. Такая последовательность называется байтом и является следующей за битом единицей измерения количества информации в компьютере.
Такая последовательность называется байтом и является следующей за битом единицей измерения количества информации в компьютере.
С помощью одного байта можно записывать двоичные коды 28 = 256 чисел от 0 до 255. Байты объединяются в последовательности длиной 1024 (=210). Такая последовательность называется килобайтом (Кбайт).
Последовательность из 1024 Кбайтов называется мегабайтом (Мбайт), из 1024 Мбайтов — гигабайтом (Гбайт), из 1024 Гбайтов — терабайтом (Тбайт).
Бит, байт, килобайт, мегабайт — основные единицы измерения количества информации в компьютере.
Итак, с помощью двоичных кодов цифры и их последовательности (числа) становятся понятными компьютеру. Процесс преобразования информации представляется в виде схемы:
Информация————->Числа—————->Двоичные коды.
Память компьютера содержит информацию только в двоичном виде (в виде 0 и 1), и ЦП выполняет действия только с данными, представленными в двоичной системе.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления — это система счисления, в которой основанием является число 16. Любое целое положительное число представляется в этой системе с помощью степеней числа 16 в виде:
Шестнадцатеричной записью целого положительного числа является последовательность коэффициентов ап an-1 … al a0 из представления (3).
Например:
Для того чтобы представление числа в шестнадцатеричной системе было однозначным, значения коэффициентов при степенях числа шестнадцать должны быть целыми числами от 0 до 15. Если значение коэффициента взять равным 16, то умножение какой-то степени числа 16 на этот коэффициент дает следующую степень числа 16: 16•16n=1•16n+1; 25•16n=(16+9) •16n=1•16n+1+9•16n.
В качестве коэффициентов для записи чисел в шестнадцатеричной системе берутся шестнадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F. Они называются шестнадцатеричными цифрами.
Они называются шестнадцатеричными цифрами.
Введение шестнадцатеричных цифр А, В, С, D, Е, F является необходимым, т.к. при использовании в качестве коэффициентов в записи шестнадцатеричных чисел 10, 11,…15 появляется неоднозначность в их прочтении.
Применение шестнадцатеричной системы счисления в информатике удобно в связи с тем, что содержимое одного байта можно записать двумя шестнадцатеричными цифрами. Действительно, для записи любой шестнадцатеричной цифры достаточно четырех битов. Максимальная шестнадцатеричная цифра F=1510 имеет двоичный код 1111. Один байт — это 8 битов, которые можно разделить на две части: четыре младших бита с номерами от 0 до 3 и четыре старших бита с номерами от 4 до 7.
Кодировка символов
Компьютеры могут обрабатывать только информацию, представленную в числовой форме. При вводе документов, текстов программ и т.д. вводимые символы кодируются определёнными числами, а при выводе их для чтения человеком (на монитор, принтер и т. д.) по каждому числу (коду символа) строится изображение символа. Соответствие между набором символов и их кодами называется кодировкой символов.
д.) по каждому числу (коду символа) строится изображение символа. Соответствие между набором символов и их кодами называется кодировкой символов.
Как правило, код символа хранится в одном байте, поэтому коды символов могут принимать значения от 0 до 255. Такие кодировки называются однобайтными, они позволяют использовать до 256 различных символов. Впрочем, в настоящее время всё большее распространение приобретает двухбайтная кодировка Unicode, в ней коды символов могут принимать значения от 0 до 65535. В этой кодировке имеются номера для практически всех применяемых символов (букв алфавитов разных языков, математических, декоративных символов и т.д.).
В графической среде Windows кодовые таблицы, разработанные для IBM PC, являются во многом устаревшими.
При использовании программ для DOS и для Windows пользователь вынужден работать с двумя различными кодировками символов: одна используется в DOS-программах, другая — в Windows-программах. В терминологии Windows первая кодировка называется OEM-кодировкой, вторая — ANSI-кодировкой. Windows содержит стандартные функции для перекодировки из OEM в ANSI и обратно. Многие Windows-программы (редакторы текстов, табличные процессоры и т.д.) при экспорте и импорте файлов в формате программ для DOS автоматически выполняют преобразование из OEM в ANSI и обратно.
В терминологии Windows первая кодировка называется OEM-кодировкой, вторая — ANSI-кодировкой. Windows содержит стандартные функции для перекодировки из OEM в ANSI и обратно. Многие Windows-программы (редакторы текстов, табличные процессоры и т.д.) при экспорте и импорте файлов в формате программ для DOS автоматически выполняют преобразование из OEM в ANSI и обратно.
Вывод
Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся другая информация (звуки, изображения и т.д.) для обработки должна быть преобразована в числовую форму. Для обработки на компьютере текстовой информации обычно при вводе в компьютер каждая буква кодируется определённым числом, а при выводе на внешние устройства для восприятия человеком по этим числам строятся соответствующие изображения букв.
Кодирование числовой информации
Введение
Если у вас возникли какие-либо вопросы при изучении темы «Кодирование числовой информации», то звоните мне и записывайтесь на первый репетиторский урок по информатике и ИКТ. На моих индивидуальных уроках мы с вами закроем текущие пробелы в ваших знаниях и прорешаем колоссальное количество всевозможных тематических упражнений.
На моих индивидуальных уроках мы с вами закроем текущие пробелы в ваших знаниях и прорешаем колоссальное количество всевозможных тематических упражнений.
Общие понятие о числовой информации
Думаю, что превалирующее число школьников и студентов знает фразу: «Математика – царица всех наук!». А как известно, математика очень интенсивно оперирует числами, цифрами и действиями над числами.
Первый счет появился много тысячелетий назад, так как даже в очень древние времена люди столкнулись с потребностью в счете. Его возникновение связано с желанием человека проинформировать своих соплеменников о количестве обнаруженных им объектов, предметов. По началу люди просто делили предметы по принципу один-много. То есть не было обозначения для двух, трех, десяти и более различных предметов. Их просто обозначали в количественном отношении как много.
Постепенно люди научились подключать к арифметическому счету пальцы на своих руках. С их помощью можно было считать до пяти, а если использовать обе руки, то до десяти различных предметов. Именно десятичная система счисления получило свое развитие на основе использования при счете пальцев рук.
Именно десятичная система счисления получило свое развитие на основе использования при счете пальцев рук.
Вернемся в настоящий временной континуум. Для современного человека знания, позволяющие считать предметы и записывать числа, являются обязательными. Арифметика изучается в школе с первого класса. Цифры, используя которые мы записываем числа, называются арабскими. Алфавит арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего десять различных цифр или состояний.
Числа можно классифицировать на две фундаментальные группы:
Каждое число из представленных групп может быть либо:
Примеры различных десятичных чисел:
-56 — целое отрицательное число;
12.78 — действительное положительное число;
0.0 — действительное число, равное нулю;
12000 — целое положительное число.
Наша цель – понять, каким образом производится кодирование числовой информации, выраженной целыми или дробными числами, которые являются положительными, отрицательными или равными нулю.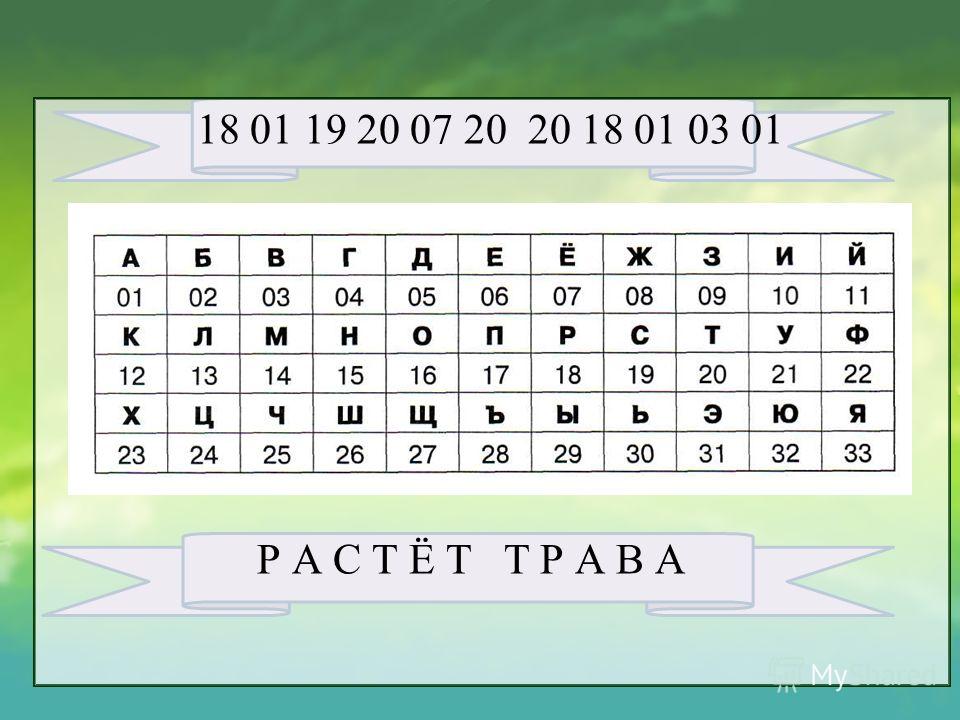 Другими словами, мы должны понять, как персональный компьютер хранит, обрабатывает, копирует числа на «своем» уровне.
Другими словами, мы должны понять, как персональный компьютер хранит, обрабатывает, копирует числа на «своем» уровне.
Свойства числовой информации
Конечность. Информация, выраженная числовым значением, должна быть конечной. Процессор персонального компьютера не сможет обработать число, которое не является конечным или завершенным. То есть прежде чем приступить к кодированию числовой информации, процессор должен быть уверен, что данное значение записано полностью и не будет изменено пользователем.
Понятность. Если мы говорим о кодировании числовой информации, которая представлена десятичным числом, то необходимо, чтобы само число состояло из элементов, которые будут понятны исполнителю при кодировании. Исполнителем является, в строгом приближении, процессор персонального компьютера. Например, число 129 состоит из трех цифр: 1, 2 и 9. Каждое из этих цифр входит в состав арабского алфавита. Если мы представим числовую информацию в виде значения 89J1’4, то подобное значение будет некорректно обработано процессором и он выдаст исключение, то есть сгенерирует ошибку.
 Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.
Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.
Приведенные два свойства являются ключевыми в алгоритмах кодирования числовой информации. Пожалуй, еще стоит отметить неосновное свойство – размер числа. Но в современном мире мощности персональных компьютеров постоянно увеличиваются и самые эффективные процессоры способы обрабатывать огромные значения.
Способы кодирования числовой информации
Сразу необходимо твердо уяснить следующее: процессор персонального компьютера взаимодействует с любыми данными исключительно на уровне цепочек, состоящих из 0 и 1. Набор нулей и единиц называют двоичным или бинарным кодом. То есть любые текстовые, символьные или числовые значения, которые понятны простому человеку, процессор преобразует в двоичный код. Следовательно, наша задача – научиться переводить числовые значения в бинарное представление, состоящее из цепочек 0 и 1.
Для полного осознания алгоритма кодирования числовой информации необходимо очень хорошо уяснить понятие «Машинное слово». Возможно вы слышали, что иногда пользователи говорят, что на их компьютерах установлена 32-х разрядная или 64-х разрядная система Microsoft Windows. Именно значение разрядности (в приведенном примере это 32 или 64) и отвечает за то, сколько бит информации будет выделено для хранения какого-либо математического значения при кодировании числовой информации. То есть, если нам дано положительное целое число 25, то при преобразовании его в бинарный код, ему будет выделено 32 или 64 бита. Также напомню, что один байт информации состоит из 8 битов.
Далее по тексту я буду работать на уровне 16-и разрядной системы. То есть любое кодирование числовой информации будет представлено с использованием машинного слова в 16 бит.
Кодирование целых положительных чисел
Это наиболее простой способ кодирования данных, так как для его реализации необходимо уметь переводить числа из десятичной системы счисления в двоичную систему. Ниже я приведу таблицу, в которой покажу кодирование целых положительных чисел различной значности.
Ниже я приведу таблицу, в которой покажу кодирование целых положительных чисел различной значности.
Исходное десятичное число | Закодированное десятичное число в двоичном коде |
5 | 0000 0000 0000 0101 |
27 | 0000 0000 0001 1011 |
870 | 0000 0011 0110 0110 |
19265 | 0100 1011 0100 0001 |
Очень внимательно посмотрите на вторую колонку данной таблицы. Как видно каждая закодированная цепочка, состоящая из нулей и единиц, имеет длину в 16 позиций. Для повышения читабельности я сгруппировал разряды на четыре группы по четыре бита в каждой группе.
Нули, которые идут слева до первой единицы, считаются незначимыми, так как они не влияют на закодированное значение и при записи бинарного кода, например в тетрадь, они как правило не выписываются. То есть двоичное представление числа 5 обычно выписывают в формате 101. Но при этом вы должны обязательно понимать, с какой длиной машинного слова было выполнено данное преобразование. В нашем примере длина машинного слова составляет 16 бит.
То есть двоичное представление числа 5 обычно выписывают в формате 101. Но при этом вы должны обязательно понимать, с какой длиной машинного слова было выполнено данное преобразование. В нашем примере длина машинного слова составляет 16 бит.
Кодирование целых отрицательных чисел
Отрицательное число отличается от положительного только наличием специального символа ‘-‘, который ставится перед началом записи числового значения. Примеры отрицательных целых чисел: -20, -3, -189.
Наша задача – понять, каким образом процессор кодирует отрицательность числовых значений. Для этого нужно вспомнить, что такое старший разряд. Старший разряд – это самый левый разряд в записи двоичного числа. Именно данный разряд играет ключевую роль при кодировании отрицательных чисел.
Фундаментальное правило: старший или самый левый разряд числа при двоичном кодировании числовой информации отводится под знак числа, а остальные разряды под хранение самого значения числа. Если старший бит имеет значение 0 – показатель кодирования положительного числа, а если имеет значение 1 – показатель кодирования отрицательного числа. Все просто!
Если старший бит имеет значение 0 – показатель кодирования положительного числа, а если имеет значение 1 – показатель кодирования отрицательного числа. Все просто!
Ниже я приведу таблицу, в которой покажу кодирование целых отрицательных чисел различной значности:
Исходное десятичное число | Закодированное десятичное число в двоичном коде |
-5 | 1000 0000 0000 0101 |
-27 | 1000 0000 0001 1011 |
-870 | 1000 0011 0110 0110 |
-19265 | 1100 1011 0100 0001 |
Если пока все понятно, то двигаемся дальше!
Представьте, что перед вами лежит листок бумаги, на котором записан следующий бинарный код: 1000 0001 0100 0111 и вас просят назвать, какое десятичное число здесь закодировано. В первую очередь вам нужно посмотреть на значение старшего разряда. Видно, что оно равно 1. Вы делаете умозаключение, что этот бит показывает то, что перед вами отрицательное целое число. Сделав перевод в десятичную систему счисления вы получаете значение -327.
В первую очередь вам нужно посмотреть на значение старшего разряда. Видно, что оно равно 1. Вы делаете умозаключение, что этот бит показывает то, что перед вами отрицательное целое число. Сделав перевод в десятичную систему счисления вы получаете значение -327.
Но где гарантии, что перед вами не закодировано какое-то огромное положительное значение. Попробуйте взять число 33095 и перевести его в бинарное представление. После кодирования мы получаем значение 1000 0001 0100 0111 равное заданному, которое было записано на листке бумаги. Странно, не правда ли?!
То есть получается нельзя однозначно сказать, какое целое число закодировано набором 1000 0001 0100 0111? Мы только что с вами получили два различных значения: -327 и 33095. На самом деле можно! Для этого вам следует уточнить у автора задания следующую информацию: положительное или отрицательное число записано в представленном бинарном коде.
Парадоксальность ситуации заключается еще в том, что процессор персонального компьютера для хранения отрицательных целых чисел использует специальную форму представления. Чтобы получить бинарный код отрицательного целого числа необходимо прибегнуть к обратному и дополнительному коду чисел. В данной статье об дополнительном и обратном коде повествования не ведется. Также можно постулировать, что все выше проведенные выкладки, справедливы для прямого кода представления двоичных чисел.
Чтобы получить бинарный код отрицательного целого числа необходимо прибегнуть к обратному и дополнительному коду чисел. В данной статье об дополнительном и обратном коде повествования не ведется. Также можно постулировать, что все выше проведенные выкладки, справедливы для прямого кода представления двоичных чисел.
Если у вас остались какие-либо вопросы по кодированию числовой информации, то записывайтесь ко мне на индивидуальный урок по информатике. На данном уроке мы с вами дополнительно рассмотрим такие понятия, как: дополнительный код, обратный код, а также научимся кодировать дробные числовые величины.
Мы познакомились с системами счисления — способами кодирования чисел. Любая информация кодируется в ЭВМ с помощью последовательностей двух цифр — 0 и 1. ЭВМ хранит и обрабатывает информацию в виде комбинации электрических сигналов: напряжение 0.4В-0.6В соответствует логическому нулю, а напряжение 2.4В-2.7В — логической единице. Так как одного байта для представления этого числа недостаточно, оно представлено в виде 2 байт или 16 бит, его дополнительный код: 1111101111000101, следовательно, -1082=1111101111000110. Первоначально в ЭВМ использовался лишь латинский алфавит. В нём 26 букв. Так что для обозначения каждой хватило бы пяти импульсов (битов). Но в тексте есть знаки препинания, десятичные цифры и др. Поэтому в первых англоязычных компьютерах байт — машинный слог — включал шесть битов. Затем семь — не только чтобы отличать большие буквы от малых, но и для увеличения числа кодов управления принтерами, сигнальными лампочками и прочим оборудованием.
Двоичное кодирование текста происходит следующим образом: при нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц на машинном языке). С 80-х годов бурно развивается технология обработки на компьютере графической информации. Компьютерная графика широко используется в компьютерном моделировании в научных исследованиях, компьютерных тренажёрах, компьютерной анимации, деловой графике, играх и т.д. В современных компьютерах разрешающая способность (количество точек на экране), а также количество цветов зависит от видеоадаптера и может изменяться программно. Следовательно, 960000 байт приблизительно равно 937,5 Кбайт.
Если человек говорит по восемь часов в день без перерыва, то за 70 лет жизни он наговорит около 10 гигабайт информации (это 5 миллионов страниц — стопка бумаги высотой 500 метров). В видеопамяти компьютера хранится битовая карта, являющаяся двоичным кодом изображения, откуда она считывается процессором (не реже 50 раз в секунду) и отображается на экран. Двоичное кодирование звуковой информации. С начала 90-х годов персональные компьютеры получили возможность работать со звуковой информацией. Каждый компьютер, имеющий звуковую плату, может сохранять в виде файлов (файл — это определённое количество информации, хранящееся на диске и имеющее имя) и воспроизводить звуковую информацию. С помощью специальных программных средств (редакторов аудио файлов) открываются широкие возможности по созданию, редактированию и прослушиванию звуковых файлов. Создаются программы распознавания речи, и появляется возможность управления компьютером голосом.
При двоичном кодировании аналогового звукового сигнала непрерывный сигнал дискретизируется, т.е. заменяется серией его отдельных выборок — отсчётов. Качество двоичного кодирования зависит от двух параметров: количества дискретных уровней сигнала и количества выборок в секунду. Количество выборок или частота дискретизации в аудиоадаптерах бывает различной: 11 кГц, 22 кГц, 44,1 кГц и др. Если количество уровней равно 65536, то на один звуковой сигнал рассчитано 16 бит (216). 16-разрядный аудиоадаптер точнее кодирует и воспроизводит звук, чем 8-разрядный. При стереофоническом звучании объём аудиофайла удваивается, при квадрофоническом звучании – учетверяется. |
«Кодирование числовой информации. Системы счисления». 10-й класс
Цели:
- познакомить с кодированием числовой информации;
- познакомить с системами счисления;
- формировать навыки работы на ПК;
- формировать общеучебные и общекультурные умения и навыки работы с информацией.
Задачи:
- Образовательные:
- закрепить материал по теме «Система счисления» и «Кодирование информации»;
- познакомить с системами счисления, используемыми в ПК для кодирования чисел;
- изучить правила перевода из десятичной системы
счисления в систему с любым основанием и
наоборот.

- Развивающие:
- развивать логическое и теоретическое мышление;
- уметь высказывать несогласие, сомнение, согласие с мнениями другого человека;
- адаптировать основные правила гигиены учебного труда к индивидуальным особенностям;
- владеть различными средствами самоконтроля и взаимоконтроля;
- развивать навыки самостоятельной работы на ПК.
- Воспитательные:
- способствовать формированию толерантного отношения к одноклассникам;
- формировать бережное отношение к техническим устройствам;
- формировать информационную культуру.
Оборудование: компьютер со стандартным набором программного обеспечения (ПО), проектор, экран, интерактивная доска, презентация.
Этапы урока:
I. Организационный момент – 1 минута.
Организационный момент – 1 минута.
II. Актуализация знаний – 5 минут.
III. Объяснение нового материала – 25
минут.
IV. Выполнение самостоятельной работы –
10 минут.
V. Домашнее задание – 2 минуты.
VI. Подведение итогов урока,
выставление оценок – 2 минуты.
ХОД УРОКА
I. Организационный момент:
– Здравствуйте, ребята, сегодня на уроке мы свами изучаем новую тему: «Кодирование числовой информации. Системы счисления». Урок будет проходить в несколько этапов. В конце урока каждый из вас получит оценку.
II. Актуализация знаний: по теме «Хранение информации»
1) Как человек хранит информацию? (В
собственной памяти или во внешних хранилищах
информации.)
2) Какими свойствами обладает память человека? (Память
человека не может долго хранить большие объёмы
информации, со временем часть информации
забывается. )
)
3) Чем память человека отличается от памяти
человечества? (Память человечества хранит весь
объём информации, накопленный с момента
появления человека. Информация хранится в
книгах, картинках, фотографиях, скульптурах и
т.д.)
4) Почему информацию, которую, мы помним наизусть
можно назвать оперативной? (Потому, что мы
можем быстро ей воспользоваться.)
5) Перечислите достоинства и недостатки хранения
информации во внутренней и внешней памяти? (Достоинства
внутренней памяти: быстрота воспроизведения
информации, а недостаток: со временем часть
информации забывается. Достоинства внешней
памяти: большие объёмы информации хранится
долго, а недостаток: для доступа к определённой
информации требуется время (например; чтобы
подготовить реферат по предмету необходимо
найти, проанализировать и выбрать подходящий
материал)).
III. Объяснение нового материала:
Слайд 2: Записать тему урока:
«Кодирование числовой информации. Система
счисления».
Система
счисления».
Слайд 3: Кодирование –
это процесс представления информации (сообщения)
в виде кода.
Всё множество символов, используемых для
кодирования, называется алфавитом
кодирования.
Слайд 4: Система счисления
– это совокупность приёмов наименований и
запись чисел.
Цифры – это специальные символы.
Алфавит системы счисления – это набор цифр
системы счисления.
Мощность алфавита – это количество цифр в
алфавите.
Слайд 5: Виды систем счисления
Различают следующие виды систем счисления:
- непозиционные системы счисления;
- позиционные системы счисления.
Слайд 6: Что такое позиционная система счисления?
Позиционная система счисления – все
цифры (её значение) зависит от положения цифры в
числе.
Основание позиционной системы
счисления – это целое число, которое равно
количеству цифр, используемых для изображения
чисел в данной системе счисления. Основание
показывает, во сколько раз изменяется
количественное значение цифры при перемещение
её в младший или старший разряд.
Примером позиционной системы счисления
является: десятичная система счисления.
Слайд 7: Развёрнутая форма числа
Развёрнутая форма числа в системе счисления с основанием q (q-ичная система счисления) записывается следующим образом:
где Aq – число в q-ичной системе счисления;
q – основание системы счисления;
n – число целых разрядов числа;
m – число дробных разрядов числа.
Слайд 8: Свёрнутая форма записи числа
Свёрнутая форма записи числа называется запись в виде:
Слайд 9: Десятичная система счисления
Основание: q = 10
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Число в десятичной системе счисления
записывается в виде суммы числового ряда
степеней (в данном случае 10), в качестве
коэффициентов которых выступают цифры данного
числа.
Слайд 10: Развёрнутая форма записи числа A10
В развёрнутой форме запись числа A10, которое содержит n целых разрядов числа и m дробных разрядов числа, имеет следующий вид:
Например:
555,5510 = 5*102 + 5*101 + 5*100 + 5*10-1
+ 5*10-2
234510 = 2*103 + 3*102 + 4*101 + 5*100
Слайд 11: Двоичная система счисления
Основание: q = 2
Алфавит: 0, 1
Число в двоичной системе счисления записывается
в виде суммы числового ряда степеней (в данном
случае 2), в качестве коэффициентов которых
выступают цифры данного числа.
Слайд 12: Развёрнутая форма записи числа A2
В развёрнутой форме запись числа A2, которое содержит n целых разрядов числа и m дробных разрядов числа, имеет следующий вид:
Например:
100010012 = 1*27 + 0*26 + 0*25 + 0*24
+ 1*23 + 0*22 + 0*21 + 1*20
10011012 = 1*26 + 0*25 + 0*24 + 1*23
+ 1*22 + 0*21 + 1*20
Слайд 13: Восьмеричная система счисления
Основание: q = 8
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
Число в восьмеричной системе счисления
записывается в виде суммы числового ряда
степеней (в данном случае 8), в качестве
коэффициентов которых выступают цифры данного
числа.
Слайд 14: Развёрнутая форма записи числа A8
В развёрнутой форме запись числа A8, которое содержит n целых разрядов числа и m дробных разрядов числа, имеет следующий вид:
Например:
7148 = 7*82 + 1*81 + 4*80
12448 = 1*83 + 2*82 + 4*81 + 4*80
Слайд 15: Шестнадцатеричная система счисления
Основание: q = 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Число в восьмеричной системе счисления записывается в виде суммы числового ряда степеней (в данном случае 16), в качестве коэффициентов которых выступают цифры данного числа.
Слайд 16: Развёрнутая форма записи числа A16
В развёрнутой форме запись числа A16, которое содержит n целых разрядов числа и m дробных разрядов числа, имеет следующий вид:
Например:
3CE16 = 3*162 + 12*161 + 14*160
75E16 = 7*162 + 5*161 + 14*160
3FC16 = 3*162 + 15*161 + 12*160
A03B16 = 10*163 + 0*162 + 3*161 + 11*160
Слайд 17: Перевод целых чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную
Перевод чисел из десятичной системы в
двоичную, восьмеричную и шестнадцатеричную
может осуществляться различными способами.
Алгоритм перевода целых десятичных чисел в двоичную, восьмеричную и шестнадцатеричную системы счисления следующий:
1. Последовательно выполнять деление исходного
целого десятичного числа и получаемых целых
частных на основании системы (на 2, 8, 16) до тех пор,
пока не получим частное, равное нулю.
2. Получить искомое двоичное, восьмеричное или
шестнадцатеричное число, для чего записать
полученные остатки обратной последовательность.
Например:
| 1910 = ––> q = 2 | |
| Остаток | |
| 19 : 2 = 9 9 : 2 = 4 4 : 2 = 2 2 : 2 = 1 |
1 1 0 0 |
Запишем остатки, начиная с последнего – 10011, то есть 4610 = 100112
| 12710 = ––> q = 8 | |
| Остаток | |
| 127 : 8 = 15 15 : 8 = 1 |
7 7 |
Запишем остатки, начиная с последнего – 177, то есть 12710 = 1778
| 46410 = ––> q = 16 | |
| Остаток | |
| 464 : 16 = 29 29 : 16 = 1 |
0 13 |
Запишем остатки, начиная с последнего – 1D0, то есть 46410 = 1D016
Слайд 18:Перевод чисел из двоичной системы счисления в восьмеричную
Для перевода из двоичной системы счисления в
восьмеричную необходимо разбить число на группы
по три цифры (триады), справа на лево, если в
последней левой группе окажется меньше чем три
разряда, то необходимо её дополнить слева нулями.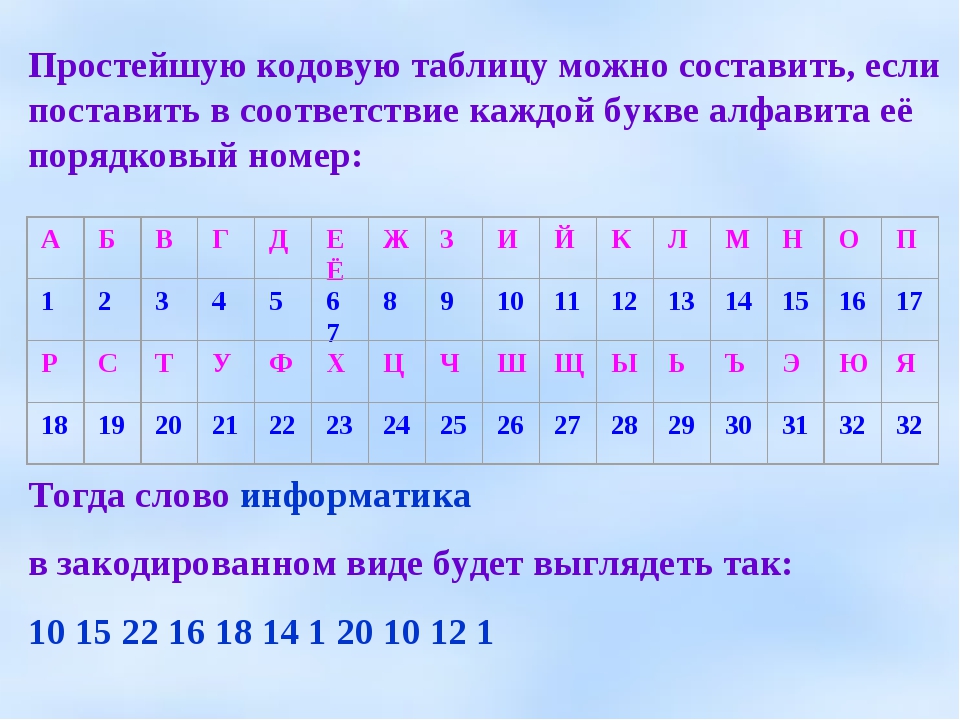
Десятичная система счисления |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Двоичные триады |
000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Например:
1010012 = 518
1101012 = 658
1001011,0112 = 113,38
Слайд 19: Перевод чисел из двоичной системы счисления в шестнадцатеричную
Для перевода целого двоичного числа в
шестнадцатеричное его нужно разбить на группы по
четыре цифры (тетрады), начиная справа; если в
последней левой группе окажется меньше разрядов,
надо дополнить её слева нулями.
Шестнадцатеричные цифры |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Двоичные тетрады |
0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Например:
1010012 = 2916
1111010101,112 = 3D5,C16
IV.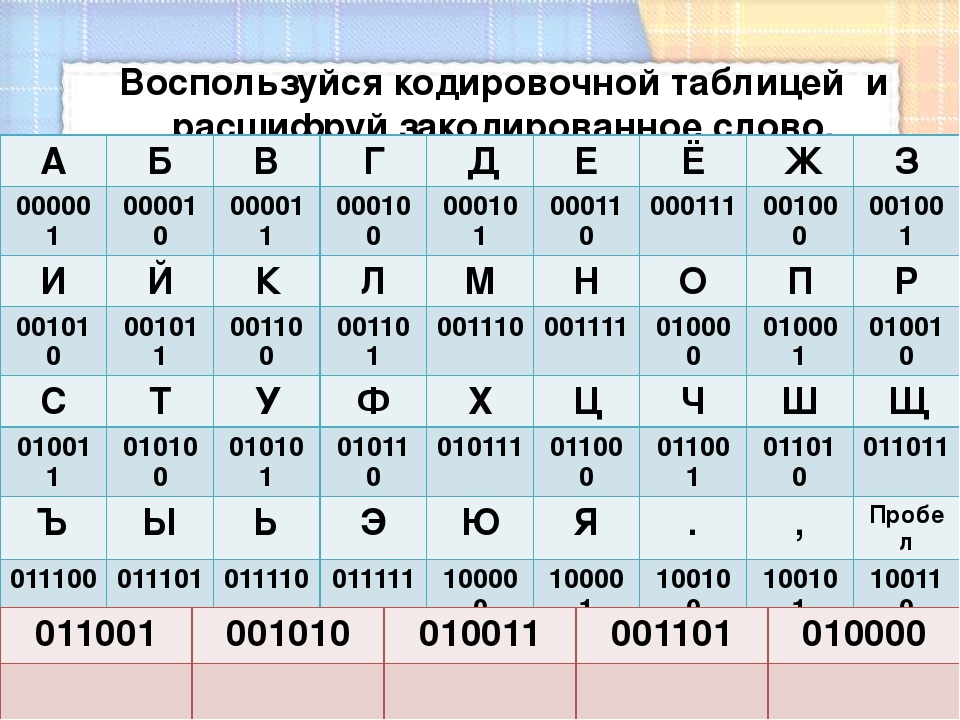 Слайд 20: Самостоятельная работа
Слайд 20: Самостоятельная работа
Задания
1. Как представлено число AB16 в двоичной системе счисления?
а) 101100112 б) 110010112 в) 101010112 г) 101001112
2. Дано число х = 248 Какое из чисел у, записанных в двоичной системе удовлетворяет условию x < y?
а) 100012 б)101002 в) 100102 г) 110002
3. Сколько единиц в двоичной записи числа 568?
а) 1 б) 2 в) 3 г) 4
4. Чему равна сумма чисел x и y при х = 10010, y = 158&
а) 11510 б) 11100012 в) 238 г) 1110002
5. Вычислите сумму чисел x и y при x = 4178
y = CA16. Результат запишите в восьмеричной
системе счисления.
Вычислите сумму чисел x и y при x = 4178
y = CA16. Результат запишите в восьмеричной
системе счисления.
6. Чему равна разность чисел 7538 – 4118, записанная в восьмеричной системе счисления?
7. В системе счисления с некоторым основанием десятичное число 10 записывается в виде 101. Укажите это основание.
8. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 1210 оканчивается на 3.
V. Слайд 21: Домашнее задание
Вопросы:
1. Дать определение систем счисления. Назвать и
охарактеризовать свойства системы счисления?
2. Какие символы используются для записи чисел в
двоичной системе счисления? Восьмеричной?
Шестнадцатеричной?
3. Преобразуйте следующие десятичные числа в
двоичные (восьмеричные, шестнадцатеричные): 0, 1, 18,
25, 128?
4. Дешифруйте следующие двоичные числа,
преобразовав их в десятичные: 00102, 10112,
111012, 01112, 01012?
Дешифруйте следующие двоичные числа,
преобразовав их в десятичные: 00102, 10112,
111012, 01112, 01012?
5. Дешифруйте следующие восьмеричные числа,
преобразовав их в десятичные: 7778, 3758,
1118, 10158?
6. Дешифруйте следующие шестнадцатеричные числа,
преобразовав их в десятичные: 1516, А616,
1А516, 6316?
VI. Подведение итогов урока, выставление оценок
За урок может быть выставлены всем оценки (за самостоятельную работу).
Использованные источники и литература:
1) М.С.Цветкова, Л.С.Великович «Информатика
и ИКТ. Учебник», Москва, Издательский центр
«Академия», 2012 год.
2) Н.Д.Угринович «Информатика и ИКТ.
Профильный уровень. Учебник для 10 класса»,
Москва, БИНОМ, Лаборатория знаний, 2011 год.
3) ЕГЭ «Информатика и ИКТ» 10 – 11 классы под
редакцией Ф.Ф.Лысенко, Л. Н.Евич, ЛЕГИОН-М,
Ростов-на-Дону, 2011 год.
4) http://comp-science.narod.ru/Demenev/files/history.htm
— История систем счисления.
5) С.С.Крылов, Д.М.Ушаков «Информатика. ЕГЭ.
Тематическая рабочая тетрадь», Издательство
«Экзамен», Москва, 2010 год.
Кодирование числовой информации
Кодирование числовой информации
Рассмотрим, как кодируется числовая
информация, для этого введем понятие системы счисления.
Система называется позиционной, если значение каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Непозиционная система- римская, позиционная- десятичная. Число единиц какого-либо разряда,
объединяемых в единицу более старшего разряда, называют основанием позиционной
системы счисления. Если количество таких цифр равно P, то система счисления
называется P-ичной. Основание системы счисления совпадает с количеством цифр,
используемых для записи чисел в этой системе счисления.
Запись произвольного числа x в P-ичной позиционной системе счисления
основывается на представлении этого числа в виде многочлена
1. При переводе чисел из
десятичной системы счисления в систему с основанием P > 1 обычно используют
следующий алгоритм:
если переводится целая часть числа, то она делится на P, после чего запоминается
остаток от деления. Полученное частное вновь делится на P, остаток запоминается.
Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки
от деления на P выписываются в порядке, обратном их получению;
если переводится дробная часть числа, то
она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь
полученная дробная часть умножается на P и т.д. Процедура продолжается до тех
пор, пока дробная часть не станет равной нулю. Целые части выписываются после
двоичной запятой в порядке их получения. Результатом может быть либо конечная,
либо периодическая двоичная дробь. Поэтому, когда дробь является периодической,
приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной
записью исходного числа в системе с основанием P.
2. При переводе чисел из системы
счисления с основанием P в десятичную систему счисления необходимо пронумеровать
разряды целой части справа налево, начиная с нулевого, и в дробной части,
начиная с разряда сразу после запятой слева направо (начальный номер -1). Затем
вычислить сумму произведений соответствующих значений разрядов на основание
системы счисления в степени, равной номеру разряда. Это и есть представление
исходного числа в десятичной системе счисления.
Числовые коды: определение и классификация
Прочитав эту статью, вы узнаете об определении и классификации числовых кодов.
Определение цифровых кодов :Представление чисел в компьютерных схемах, регистрах и блоке памяти с помощью электрических сигналов или магнетизма называется ЧИСЛОВОЙ КОДИРОВКОЙ. В компьютерной системе числа хранятся в двоичной форме, поскольку любое число может быть представлено с использованием только единиц и нулей.Двоичная 1 может быть представлена наличием импульса напряжения или тока или магнетизма, а двоичная 0 — отсутствием его.
Некоторые блоки памяти используют восемь крошечных магнитных колец из ферритового материала в каждом месте. Намагниченное кольцо представляет 1, а немагнитное кольцо — 0. Каждое такое кольцо называется BIT, что является сокращением от BINARY DIGIT.
Вместо ферритовых колец в качестве битов памяти можно использовать полупроводники. Если они проводят, они будут представлять двоичную единицу, иначе 0.В некоторых модулях памяти вместо полупроводников используются электронные устройства, известные как FLIP-FLOPS. Триггеры имеют вывод Q. Заряд на этом выводе представляет двоичную 1 и отсутствие заряда 0.
Вместо триггеров в блоках памяти можно использовать конденсаторы (конденсаторы). В таком случае заряженный конденсатор будет представлять двоичную единицу и разряженный конденсатор 0. На ранних этапах развития компьютеров и блоков памяти было предпринято несколько попыток сконфигурировать числа в них с использованием двоичных цифр.Эти конфигурации известны как ЧИСЛОВЫЕ КОДЫ.
Классификация цифровых кодов :Цифровые коды в целом классифицируются как:
(i) взвешенные коды и
(ii) Невзвешенные коды.
Во взвешенном коде каждый бит числа имеет значение, зависящее от его положения или расположения в числе, и это значение называется весом. Десятичное значение числа будет равно сумме произведения битов и их соответствующих весов.В невзвешенных кодах сохраненное десятичное число не будет равно значению битовой конфигурации.
а. Взвешенные коды :Различные типы взвешенных кодов:
(i) Код BCD,
(ii) 2-4-2-1 Код,
(iii) 4-2-2-1 Код,
(iv) 5-2-1-1 Код,
(v) 7-4-2-1 Код и
(vi) 8-4-2-1 Код.
Код BCD :
BCD означает ДЕСЯТИЧНОЕ ЧИСЛО с ДВОЙНЫМ КОДОМ.В этом коде десятичная цифра выражается в виде 4 БИТОВ (двоичных цифр). Младший бит имеет вес 2 °, следующий бит слева 2 1 , следующий слева 2 2 и самый старший бит 2 3 (см. Таблицу 3.1). Некоторые из самых ранних версий компьютеров использовали этот код для хранения цифр от 0 до 9.
Позже было обнаружено, что используя 4 бита, можно сохранять числа до 15 (F в шестнадцатеричном формате). Так началась практика хранения в шестнадцатеричной форме.В указанных местах могут храниться более крупные числа, если они представлены в шестнадцатеричной форме, чем в десятичной.
Прочие взвешенные коды :
Другие типы взвешенных кодов приведены в таблице 3.2. Из них код 8 4 2 1 имеет два бита, а именно 2 и 1, которые имеют отрицательные веса.
Вышеупомянутые коды были некоторыми из кодов, которые были протестированы во время эволюции цифровых компьютеров. Сейчас они не имеют большого значения.
г. Невзвешенные коды :
Невзвешенные коды бывают двух типов, а именно:
(i) Коды без обнаружения ошибок и,
(ii) Коды обнаружения ошибок.
Коды без обнаружения ошибок :
Коды отсутствия ошибок:
(i) СЧЕТЧИК КОЛЬЦЕВ Код,
(ii) Код EXCESS THREE и
(iii) СЕРЫЙ код.
Код счетчика звонков :
Этот тип кода использовался в первом в мире электронно-цифровом компьютере ENIAC. Для представления любой цифры от 0 до 9 используется всего ДЕСЯТЬ битов (см. Таблицу 3.3). Можно отметить, что, хотя используются 10 бит, только один бит будет «включен» за раз.
Превышение тройки Код :
Это двоичный код, в котором каждое десятичное число выражается больше трех, т.е.e, 3 добавляется к десятичному числу, а затем кодируется в двоичные цифры, например, чтобы получить дополнительный тройной код 4, к нему добавляется 3, что дает 7. BCD-код 7, а именно 0111 будет 4 в избытке Три кода (см. Таблицу 3.4). Код лишних трех называется самодополняющимся кодом.
Дополнение к любой отдельной цифре в любой системе счисления — это разница между максимальным значением отдельного символа в этой системе и рассматриваемым числом (например,g.,) В десятичной системе дополнительное число 6 равно 3 (т. е.) (9-6). Таким образом, дополнение до 3 будет 6.
В двоичном коде 1 и 0 дополняют друг друга. Код BCD не является самодополняющимся кодом в том смысле, что дополнение двоичной формы десятичного числа не будет его дополнением десятичной формы, (например,) 6 в коде BCD равно 0110; дополнение этой двоичной формы получается заменой всех l на 0 и наоборот. В данном случае это будет 1001, то есть 9 в десятичной системе, а не 3.
Десятичная цифра 6 будет выражена в коде превышения трех как 1001. Его двоичное дополнение — 0110. Оно представляет 3 в самом коде превышения трех. Это относится ко всем десятичным цифрам от 0 до 9 (см. Таблицу 3.4). Из-за этого код превышения трех считается самодополняющимся.
Серый код :
Другие названия этого кода:
(i) КОД РАССТОЯНИЯ УСТАНОВКИ,
(ii) ЦИКЛИЧЕСКИЙ КОД и
(iii) ОТРАЖЕННЫЙ КОД.
Он называется кодом единичного расстояния, потому что РАССТОЯНИЕ между двоичными формами любых двух соседних чисел всегда будет равно единице.
Расстояние Хэмминга любых двух чисел равной длины в двоичной форме определяется как количество позиций, на которые они различаются. Например, двоично-десятичный код 7 — 0111, а код 8 — 1000. Расстояние Хэмминга между ними равно 4, поскольку они различаются всеми четырьмя цифрами.
То же 7 в коде Грея будет 0100, а 8 будет 1100, а расстояние Хэмминга между ними в этом коде равно 1.Из таблицы 3.5 видно, что расстояние Хэмминга любых двух последовательных чисел (от 0 до 9) в коде Грея всегда равно 1.
Десятичный код Грея можно получить из его двоично-десятичного кода следующим образом:
(i) Запишите его форму кода BCD;
(ii) Старший бит в коде Грея такой же, как в коде BCD;
(iii) Второй и последующие биты в коде Грея будут суммой бита в позиции и предыдущей позиции в BCD-коде.
При расчете суммы необходимо соблюдать следующие правила:
(i) 0 + 0 = 0;
(ii) 0 + 1 = 1;
(iii) 1 + 1 = 0 (с переносом 1, которым следует пренебречь).
Пример 3.1:
Найдите код Грея десятичного числа 5.
Обратите внимание, что этот метод не применим к десятичному числу 9. Его код Грея будет 1000, а не 1101. Он принят для поддержания расстояния Хэмминга 1 между 9 и 0.
В электронных схемах устройства, известные как ворота XOR, используются для преобразования кода BCD в код Грея.
Чтобы преобразовать число из кода Грея в код BCD, необходимо выполнить следующие шаги:
(i) Старший бит в коде BCD такой же, как и в коде Грея.
(ii) Каждый второй и последующий биты будут суммой соответствующего бита в коде Грея и предыдущего бита в BCD-коде. Правила сложения такие же, как и для преобразования BCD в код Грея.
Пример 3.2:
Найдите десятичное значение числа 1100 кода Грея.
Код Грея
полезен при преобразовании различных аналоговых сигналов в цифровую форму, поскольку только один bi изменяется от одного кода к другому.
Коды обнаружения ошибок :
Это 2 типа, а именно:
(i) КОДЫ ПРОВЕРКИ ОШИБОК и
(ii) КОДЫ ИСПРАВЛЕНИЯ ОШИБОК.
Коды проверки ошибок :
Это 2 категории, а именно:
(i) КОДЫ САМОПРОВЕРКИ и
(ii) КОДЫ ПРОВЕРКИ ЧЕТНОСТИ.
В этом типе кода, хотя конфигурация битов будет отличаться для разных цифр (от 0 до 9), количество 1 битов будет одинаковым для всех цифр. К этой категории относятся БИКИНАРНЫЙ КОД и «Код 2 из 5». В них общее количество 1 Бита в конфигурации любого числа всегда равно 2 (см. Таблицу 3.6).
Из-за этого любая ошибка из-за отказа или отсутствия какого-либо бита может быть легко распознана. Бинарный кодекс был принят в японском ABACUS, который назывался SOROBAN.Но сейчас он не используется, так как у него немного веса 5. Таким образом, «код 2 из 5» не используется, так как он имеет небольшой вес 7.
Коды проверки четности :
Существует 2 типа кодов ПРОВЕРКИ ЧЕТНОСТИ, а именно:
(i) КОД НЕЧЕТНОЙ ЧЕТНОСТИ и
(ii) ЧЕТНЫЙ КОД ЧЕТНОСТИ.
В обоих этих кодах, помимо числовых битов, используется дополнительный бит. Этот бит называется БИТОМ ЧЕТНОСТИ или КОНТРОЛЬНЫМ БИТОМ.Система кодирования может быть разработана либо для нечетной четности, либо для четности.
Если разработан для нечетной четности, бит четности будет автоматически сгенерирован, если число 1 бит в числовом коде четное. Точно так же, если он разработан для контроля четности, бит четности будет автоматически сгенерирован, если количество единиц в числовых битах нечетное (см. Таблицу 3.7). Большинство компьютеров рассчитаны на нечетную четность.
В таблице 3.7 D 0 , D 1 , D 2 и D 3 обозначают числовые биты с весами 2 °, 2 1 , 2 2 и 2 3 соответственно .P 0 обозначает бит нечетной четности, а P e бит четности. Можно отметить, что ноль представлен как 8 2 в четной битовой конфигурации.
Коды проверки ошибок :
К этой классификации относятся следующие типы кодов:
(i) Простой код исправления ошибок,
(ii) самокорректирующийся код и
(iii) Код Хэмминга.
Простой код исправления ошибок :
Используется для записи данных на магнитные ленты.В них данные записываются на 7 или 9 треков. В 9-дорожечной системе символы записываются с помощью магнитных пятен на 8 дорожках. Конфигурация этих пятен будет разной для разных персонажей. Девятая дорожка функционирует как дорожка четности. В системе, разработанной для нечетной четности, 9-я дорожка будет активирована, если необходимо, в столбце для поддержания нечетной четности.
Помимо этого, для каждого элемента данных на каждой дорожке создается КОНТРОЛЬНЫЙ БИТ, чтобы также поддерживать нечетную четность на каждой дорожке.В таблице 3.8 показано, как десятичное число 5384 будет записано на ленту в коде EBCDIC и как биты четности и проверки будут генерироваться вдоль столбца и дорожки / строки соответственно.
Самокорректирующийся код :
Этот код также применяется в случае записи данных на Магнитные ленты. Каждый символ записывается нечетное количество раз (3 или 5 раз) в соседние столбцы. В случае, если символ в любом из столбцов не разборчив — из-за царапин или образования пыли на поверхности ленты ИЛИ он отличается от символа в соседних столбцах — компьютер предназначен для приема данных в большинстве случаев. колонн.
Например, в таблице 3.9 показана запись символа 7 в коде ASCII в трех последовательных столбцах, а не только один раз. Если запись в какой-либо точке размыта (точка, отмеченная X), процессор считывает данные из основной конфигурации.
Код Хэмминга :
КодыХэмминга названы в честь Р. Хэмминга, который сформулировал метод множественной проверки на четность. Пусть P 0 , P 1 — — и т. Д. P n — биты четности, используемые в коде.Они будут разбросаны по сообщению (т. Е.) Среди взвешенных битов, скажем, D 0 , D 1 — — и т. Д. D m , представляющих символ.
Требуемая нечетная или четная конфигурация будет разработана для поддержки различных комбинаций. Пример 3.3 иллюстрирует метод формулирования типа кода Хэмминга.
Пример 3.3:
Три бита четности должны быть разработаны для проверки ошибок в десятичных числах, закодированных в двоично-десятичном коде.Эти биты должны быть распределены между взвешенными битами. Если взвешенные биты обозначены как D 0 , D 1 , D 2 и D 3 , а биты четности P o , P 1 и P 2 , код Хэмминга должен быть разработаны для четности ODD для каждой из следующих комбинаций: (i) P 0 , P 1 , P 2 и D 2 , (ii) P 1 , D o , D 2 и D 3 , и (iii) P 1 , D 1 , D 2 и D 3 .
Решение:
Поскольку биты четности должны быть распределены между взвешенными битами, конфигурация будет D 3 , P 2 , D 2 , P 1 , D 1 , P 0 и D 0 .
Способ представления десятичных чисел вышеуказанными битами с сохранением нечетной четности для данных комбинаций приведен в таблице 3.10.
Примечание:
Неправильная четность в одной или нескольких комбинациях указывает на состояние ошибки.
(PDF) Числовое кодирование номинальных данных
Зенон Гняздовски, Михал Грабовски
Хорошо известная идея фольклорного типа представляет собой m-значную номинальную область как равноотстоящие
точек в пространстве Евклида. Таким образом, классический евклидов подход представляет векторы
номинальных значений как точки в пространстве Rq, где q равно сумме мощностей номинальных
рассматриваемых областей. Предлагаемая кодировка представляет векторы номинальных значений как
точек в Csspace, где s равно количеству рассматриваемых номинальных доменов.Мы думаем, что наше кодирование можно рассматривать как одну из альтернатив, когда анализируемые непрерывные — номинальные данные
чувствительны к ходу размерности (см. [6], [7]) из-за низкой (по сравнению с
евклидовым кодированием). ) размерность конечного пространства кодов.
Совершенно очевидно, что предлагаемая кодировка вводит дополнительную информацию. Например, симметрии
кодов номинальных данных с равными частотами специфичны для предлагаемой схемы кодирования
, и может случиться так, что симметрии исходных данных будут отличаться от симметрий
их кодов.Тем не менее, другие схемы кодирования, включающие номинальные частоты данных
,информации, например байесовское кодирование номинальных значений посредством скоринга (см. [8]), также подвержены этому недостатку. Более того, байесовское кодирование путем скоринга применимо только для обучения
наборов данных с двумя категориями решений. Наше предложение является полностью общим и может быть применено к наборам данных
без какой-либо информации о категориях решений.
Анализируемый в этой статье набор данных показывает, что классификация с использованием кодированных номинальных данных
или как числовых, так и кодированных номинальных данных более эффективна, чем классификация, которая
использует специальное кодирование или только числовые данные.Отсюда следует сделать вывод, что информация
, содержащаяся в закодированных номинальных данных, важна для классификации.
Представленное предложение является предварительным. Хотя метод выглядит интересным, необходимы дальнейшие исследования этого подхода, например серьезное экспериментальное исследование.
Эти исследования могут подтвердить полезность метода. Они также могут показать другие
возможных применений предложенного метода.
Ссылки
[1] М. Грабовски и М. Корпусик. Метрики и сходства в моделировании зависимостей между непрерывными и номинальными данными. Zeszyty Naukowe WWSI, 7 (10): 25–37, 2013.
[2] З. Гняздовский. Цифровое кодирование номинальных данных. Семинар, Варшавская школа компьютеров
Science, 15 мая 2014 г.
[3] Ф. Вилкоксон. Индивидуальные сравнения методами ранжирования. Бюллетень биометрии, 1 (6): 80–83,
1945.
[4] С. Г. Крейн.Analiza funkcjonalna. PWN, Warszawa, 1967.
[5] L. Rutkowski. Методы и техники sztucznej inteligencji. Wydawnictwo Naukowe PWN,
Warszawa, 2012.
[6] Т. Хасти, Р. Тибширани и Дж. Фридман. Элементы статистического обучения. Springer,
New York, 2001.
[7] Р. Беллман. Адаптивные процессы управления. Экскурсия. Princeton University Press,
Princeton, 1961.
60
Цифровой код в числовые данные
Minitab можно использовать для преобразования или «кодирования» столбца чисел в другой столбец чисел.Эта процедура особенно полезна для создания фиктивных индикаторных переменных для качественных переменных-предикторов, которые вы хотите включить в свою регрессионную модель.
Процедура Minitab
- В Minitab выберите Данные >> Перекодировать >> в числовой …
- В поле с надписью ‘ Перекодировать значения в следующих столбцах ‘ укажите имя числовой переменной, которую вы хотите закодировать.
- В поле Method укажите метод перекодирования значений, указанных выше.
- Например, чтобы перекодировать диапазоны значений, введите числовые значения в поля, обозначенные Нижняя конечная точка и Верхняя конечная точка и Перекодированное значение , которые вы хотите, чтобы этот диапазон представлял. Убедитесь, что вы сделали это для всех возможных значений переменной, которую хотите закодировать.
- Выберите ОК . Новая переменная должна появиться на вашем листе.
Примечание: , если вам нужно создать более одной числовой переменной, вы должны кодировать каждую из них отдельно.
Пример
Sports Illustrated опубликовал результаты исследования, направленного на определение того, насколько хорошо профессиональные игроки в гольф наносят удары. Набор данных puttgolf.txt содержит данные о длинах паттов ( x ) и процент успешных паттов ( y ), выполненных профессиональными гольфистами в течение 15 турниров. В набор данных включены только патты, которые находились на расстоянии от 2 до 20 футов от лунки.При подгонке к данным двухэлементной функции кусочно-линейной регрессии, соединенной с соотношением x = 10, к данным необходимо создать новую числовую фиктивную переменную, скажем « фиктивная », которая принимает значение 0, если x ≤ 10 и 1, если x > 10. Используйте Minitab, чтобы закодировать числовую переменную длиной в числовую переменную фиктивную .
Диалоговое окно Minitab Результирующий рабочий лист MinitabВидеообзор
Эффективное кодирование
Одним из способов более точного и эффективного ввода данных является грамотное использование различных кодов.Процесс преобразования неоднозначных или громоздких данных в короткие, легко вводимые цифры или буквы называется кодированием (не путать с программным кодированием). Кодирование помогает системному аналитику в достижении цели эффективности, поскольку кодированные данные требуют меньше времени для ввода людьми и, таким образом, сокращают количество вводимых элементов. Кодирование также может помочь в соответствующей сортировке данных на более позднем этапе процесса преобразования данных.
Кроме того, закодированные данные могут сэкономить ценную память и место для хранения.В общем, кодирование — это способ быть красноречивым, но лаконичным при сборе данных. Помимо обеспечения точности и эффективности, коды должны иметь цель, которая поддерживает пользователей. Определенные типы кодов позволяют нам обрабатывать данные определенным образом. Человеческие цели кодирования включают следующее:
- Отслеживание чего-либо.
- Классифицирующая информация.
- Скрытие информации.
- Раскрывающая информация.
- Требуется соответствующее действие.
Каждая из этих целей кодирования обсуждается в следующих разделах вместе с некоторыми примерами кодов.
Отслеживание чего-либо
Иногда мы хотим просто идентифицировать человека, место или вещь, просто чтобы отслеживать это. Например, магазин, производящий мягкую мебель на заказ, должен присвоить проекту номер задания. Продавцу необходимо знать имя и адрес покупателя, но менеджеру мастерской или рабочим, которые собирают мебель, необязательно знать, кто такой покупатель. Следовательно, работе присваивается произвольный номер. Число может быть случайным или последовательным, как описано в следующем подразделе.
КОДЫ ПРОСТОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Код простой последовательности — это номер, который присваивается чему-либо, если его необходимо пронумеровать. Следовательно, это не имеет отношения к самим данным. На рисунке ниже показано, как заказам производителя мебели присваивается номер заказа. С помощью этого простого ссылочного номера компания может отслеживать выполнение заказа. Работа «5676» эффективнее, чем «это коричнево-черное кресло-качалка с кожаным сиденьем для Артура Хука-младшего». Использование кода последовательности вместо случайного числа имеет некоторые преимущества.Во-первых, это исключает возможность присвоения одного и того же номера. Во-вторых, он дает пользователям приблизительное представление о том, когда был получен заказ.
Использование простого кода последовательности для обозначения последовательности поступления заказов в магазин нестандартной мебели.Коды последовательности следует использовать, когда порядок обработки требует знания последовательности, в которой элементы входят в систему, или порядка, в котором разворачиваются события. Пример можно найти в ситуации, когда банк проводит специальную рекламную кампанию, в которой важно знать, когда человек подал заявку на получение специального жилищного кредита под низкие проценты, потому что (при прочих равных) специальные ипотечные кредиты будут предоставлены на в порядке очереди.В этом случае важно присвоить каждому кандидату правильный код последовательности.
АЛФАВИТНЫЕ ПРОИЗВОДНЫЕ КОДЫ
Иногда нежелательно использовать коды последовательности. Самый очевидный случай — это когда вы не хотите, чтобы кто-то читал код, чтобы выяснить, сколько номеров было присвоено. Другая ситуация, в которой коды последовательности могут быть бесполезны, — это когда желателен более сложный код, чтобы избежать дорогостоящей ошибки. Одна из возможных ошибок — добавить платеж на счет 223, когда вы хотели добавить его в счет 224, потому что вы ввели неправильную цифру.
Буквенный производный код — это обычно используемый подход для определения номера счета. Пример, показанный на рисунке ниже, взят из почтового лейбла журнала. Код становится номером счета. Первые пять цифр образуются из первых пяти цифр почтового индекса абонента, следующие три — это первые три согласных в имени абонента, следующие четыре цифры — это адрес улицы, а последние три составляют код журнала. . Основная цель этого кода — идентифицировать учетную запись.
Идентификация учетной записи подписчика журнала с помощью буквенного производного кода.Второстепенное назначение — печать почтовых этикеток. При разработке этого кода почтовый индекс является первой частью номера счета. Записи о подписчиках обычно обновляются только один раз в год, но основная цель записей — печатать почтовые этикетки один раз в месяц или один раз в неделю. Наличие почтового индекса в качестве первой части поля первичного ключа означает, что записи не нужно сортировать по почтовому индексу для массовой рассылки, поскольку записи в файле хранятся в последовательности первичных ключей.Обратите внимание, что дата истечения срока действия не является частью номера счета, потому что этот номер может меняться чаще, чем другие данные.
Один из недостатков буквенного производного кода возникает, когда буквенная часть мала (например, имя По) или когда имя содержит меньше согласных, чем требует код. Имя Roe имеет только один согласный звук и должно быть получено как RXX или получено с использованием какой-либо другой схемы. Еще один недостаток — некоторые данные могут измениться.Изменение адреса или имени приведет к изменению первичного ключа файла.
Классифицирующая информация
Классификация дает возможность различать классы предметов. Классификации необходимы для многих целей, например, чтобы отразить, какие части плана медицинского страхования имеет сотрудник, или показать, какой студент выполнил основные требования своей курсовой работы. Чтобы классы были полезными, они должны быть взаимоисключающими. Например, если студент учится в классе F, то есть первокурсник, набрав от 0 до 36 кредитных часов, он или она также не должны классифицироваться как второкурсник (S).Перекрывающиеся классы будут F 0 36 кредитных часов, S 32 64 кредитных часа и так далее. Данные нечеткие и не так легко интерпретируемые, если классы кодирования не исключают друг друга.
КОДЫ КЛАССИФИКАЦИИ
Коды классификации используются для различения одной группы данных с особыми характеристиками от другой. Коды классификации могут состоять либо из одной буквы, либо из числа. Это сокращенный способ описания человека, места, вещи или события.
Классификационные коды перечислены в руководствах или опубликованы, чтобы пользователи могли легко их найти.Часто пользователи настолько знакомы с часто используемыми кодами, что запоминают их. Пользователь классифицирует элемент, а затем вводит его код непосредственно в онлайн-систему.
Пример классификационного кодирования — это способ, которым вы можете сгруппировать объекты, не облагаемые налогом, с целью уплаты налогов на прибыль. На рисунке ниже показано, как разрабатываются коды для таких статей, как проценты, медицинские выплаты, взносы и т. Д. Система кодирования проста: возьмите первую букву каждой из категорий; взносы — C, процентные платежи — I, поставки — S.
Группировка статей, подлежащих вычету из налогооблагаемой базы, с помощью однобуквенного классификационного кода.Все идет хорошо, пока мы не дойдем до других категорий (таких как компьютерные товары, страховые выплаты и подписки), которые начинаются с тех же букв, которые мы использовали ранее. На рисунке ниже показано, что происходит в этом случае. Кодировка была расширена, так что мы могли использовать P для «компьютера», N для «iNsurance» и B для «подписки». Очевидно, что эта ситуация далека от совершенства. Один из способов избежать такой путаницы — разрешить использование кодов длиной более одной буквы, что обсуждается далее в этой главе под заголовком мнемонических кодов.Выпадающие меню в системе с графическим интерфейсом часто используют коды классификации в качестве ярлыка для запуска функций меню, таких как Alt-F для меню «Файл».
Проблемы при использовании однобуквенного кода классификации возникают, когда категории имеют одну и ту же букву.КОДЫ ПОСЛЕДОВАТЕЛЬНОСТИ БЛОКА
Ранее мы обсуждали коды последовательности. Код последовательности блоков является расширением кода последовательности. На рисунке ниже показано, как бизнес-пользователь присваивает номера компьютерному программному обеспечению. Основные категории программного обеспечения — это браузеры, пакеты баз данных и веб-дизайн.Им были присвоены порядковые номера в следующих «блоках» или диапазонах: браузер, 100–199; база данных, 200–299; и так далее. Преимущество кода последовательности блоков состоит в том, что данные сгруппированы в соответствии с общими характеристиками, но при этом используется простота присвоения следующего доступного номера (в пределах блока, конечно) следующему элементу, нуждающемуся в идентификации.
Использование кода последовательности блоков для группировки похожих пакетов программного обеспеченияСокрытие информации
Коды могут использоваться для сокрытия или маскировки информации, которую мы не хотим, чтобы другие знали.Есть много причин, по которым бизнес-пользователь может захотеть это сделать. Например, корпорация может не захотеть, чтобы к информации в личном деле имели доступ сотрудники, занимающиеся вводом данных. Магазин может захотеть, чтобы его продавцы знали оптовую цену, чтобы показать им, насколько низкую цену они могут согласовать, но они могут закодировать ее в ценовых билетах, чтобы покупатели не узнали об этом. Ресторан может захотеть получить информацию об услуге, не сообщая клиенту имя сервера. Скрытие информации и безопасность стали очень важными в последние несколько лет.Корпорации начали предоставлять поставщикам и клиентам прямой доступ к своим базам данных, а обработка бизнес-транзакций через Интернет вызвала необходимость разработки надежных схем шифрования. В следующем подразделе описан пример сокрытия информации с помощью кодов.
ШИФРОВЫЕ КОДЫ
Возможно, самый простой метод кодирования — это прямая замена одной буквы на другую, одного числа на другое или одной буквы на число. Популярный тип головоломки, называемый криптограммой, является примером подстановки букв.На рисунке ниже показан пример шифровального кода, взятого из универмага в Буффало, штат Нью-Йорк, который закодировал все уцененные цены словами BLEACH MIND. Никто особо не помнил, почему были выбраны эти слова, но все сотрудники знали их наизусть, и поэтому шифровальный код был успешным. Обратите внимание на этот рисунок, что товар с розничной ценой 25,00 долларов будет иметь уценку BIMC, или 18,75 доллара при буквенном декодировании.
Кодирование цен со скидкой с помощью шифровального кода — это способ скрыть информацию о ценах от покупателей.Раскрытие информации
Иногда желательно раскрыть информацию конкретным пользователям с помощью кода. В магазине одежды информация об отделе, продукте, цвете и размере печатается вместе с ценой на билете для каждого предмета. Эта информация помогает продавцам и складам найти место для товара.
Другая причина раскрытия информации с помощью кодов — сделать ввод данных более значимым для людей. Знакомый номер детали, название или описание позволяет вводить более точные данные.Примеры кодов в следующем подразделе объясняют, как эти концепции могут быть реализованы.
ПОДНАБОРНЫЕ КОДЫ ЗНАЧИХ ЦИФРОВ
Когда продукт можно описать на основании его принадлежности ко многим подгруппам, мы можем использовать код подмножества значащих цифр, чтобы помочь описать его. Пример ценового билета магазина одежды на рисунке ниже является примером эффективного кода подмножества значащих цифр.
Использование кода подмножества значащих цифр помогает сотрудникам находить товары, принадлежащие определенному отделу.Случайному наблюдателю или покупателю описание позиции представляется одним длинным числом. Однако для одного из продавцов число состоит из нескольких меньших чисел, каждое из которых имеет собственное значение. Первые три цифры обозначают отдел, следующие три — продукт, следующие две — цвет, а последние две — размер.
Коды подмножества значащих цифр могут состоять либо из информации, которая фактически описывает продукт (например, число 10 означает размер 10), либо из чисел, которые назначаются произвольно (например, 202 назначается для обозначения родильного отделения).В этом случае преимущество использования кода подмножества значащих цифр состоит в том, что он позволяет находить элементы, принадлежащие к определенной группе или классу. Например, если менеджер магазина решил пометить все зимние товары для предстоящей распродажи, продавцы могут найти все товары, принадлежащие отделам с 310 по 449, блок кодов, используемый для обозначения «зима» в целом.
МНЕМОНИЧЕСКИЕ КОДЫ
Мнемоника (произносится nî-môn-ïk) — это средство для запоминания человека. Любой код, который помогает либо человеку, вводящему данные, вспомнить, как вводить данные, либо пользователю запомнить, как использовать информацию, можно рассматривать как мнемонику.Использование комбинации букв и символов дает поразительно четкий способ кодирования продукта, так что код легко увидеть и понять. Коды городских больниц, ранее использовавшиеся Региональным центром крови Буффало, были мнемоническими, как показано на рисунке ниже. Простые коды были изобретены именно потому, что администраторы центров крови и системные аналитики хотели, чтобы коды больниц было легко запоминать и вспоминать. Мнемонические коды для больниц помогли снизить вероятность доставки крови в неправильную больницу.
Мнемонические коды функционируют как вспомогательные средства запоминания, используя осмысленную комбинацию букв и цифр.Unicode
Коды позволяют нам обнаруживать символы, которые мы обычно не можем вводить или просматривать. Традиционные клавиатуры поддерживают наборы символов, знакомые людям, использующим символы западного алфавита (называемые латинскими символами), но многие языки, такие как греческий, японский, китайский или иврит, не используют западный алфавит. В этих языках могут использоваться греческие буквы, глифы или символы, представляющие слоги или целые слова.Международная организация по стандартизации (ISO) определила набор символов Unicode, который включает все стандартные языковые символы и имеет место для 65 535 символов. Вы можете отображать веб-страницы, написанные на других алфавитах, загрузив редактор метода ввода от Microsoft.
Символы глифов представлены с помощью символа «& # xnnnn;» нотация, в которой nnnn представляет конкретную букву или символ, а x означает, что для представления символов Юникода используется шестнадцатеричная нотация или нумерация по основанию 16.Например, B3 представляет собой японский символ катакана ко. Код, используемый для японского слова «привет», коничива, — こ に ち わ. На японском языке это слово выглядит так:
Полный набор символов Unicode сгруппирован по языкам и может быть найден на сайте www.unicode.org.
Запрос соответствующего действия
Коды часто необходимы, чтобы проинструктировать компьютер или лицо, принимающее решение, о том, какие действия следует предпринять. Такие коды обычно называются функциональными кодами и обычно имеют форму последовательностей или мнемонических кодов.
КОДЫ ФУНКЦИЙ
Функции, которые аналитик или программист хочет, чтобы компьютер выполнял с данными, фиксируются в кодах функций. Точное описание того, какие действия должны быть выполнены, переводится в короткий числовой или буквенно-цифровой код.
На рисунке ниже показаны примеры кода функции для обновления инвентаризации. Предположим, вы управляете молочным отделом; если упаковка с йогуртом испортилась, вы должны использовать код 3 для обозначения этого события. Конечно, данные, необходимые для ввода, различаются в зависимости от того, какая функция нужна.Например, для добавления или обновления записи потребуется только ключ записи и код функции, тогда как добавление новой записи потребует ввода всех элементов данных, включая код функции.
Коды функций компактно фиксируют функции, которые компьютер должен выполнять.
|
|
ASCII (Американский стандартный код для обмена информацией) Определение
означает «Американский стандартный код обмена информацией».»ASCII — это кодировка символов, в которой для представления символов используются числовые коды. К ним относятся прописные и строчные английские буквы, цифры и знаки пунктуации.
Стандартный ASCII
Стандартный ASCII может представлять 128 символов. Он использует 7 бит для представления каждого символа, поскольку первый бит байта всегда равен 0. Например, заглавная «T» представлена числом 84 или 01010100 в двоичном формате. Строчная буква «t» представлена как 116 или 01110100 в двоичном формате. Другие клавиши клавиатуры также сопоставляются со стандартными значениями ASCII.Например, клавиша Escape (ESC) — 27 в ASCII, а клавиша Delete (DEL) — 127.
Коды ASCII также могут отображаться как шестнадцатеричные значения вместо десятичных чисел (от 0 до 127), перечисленных выше. Например, значение ASCII клавиши Escape (27) в шестнадцатеричном формате — 1B. Шестнадцатеричное значение клавиши удаления (127) — 7F.Расширенный ASCII
128 (2 7 ) символов, поддерживаемых стандартным ASCII, достаточно для представления всех стандартных английских букв, цифр и знаков препинания.Однако недостаточно представить все специальные символы и символы из других языков. Расширенный ASCII помогает решить эту проблему, добавляя дополнительные 128 значений, в общей сложности 256 (2 8 ) символов. Дополнительные двоичные значения начинаются с 1 вместо 0. Например, в расширенном ASCII символ «é» представлен 233 или 11101001 в двоичном формате. Заглавная буква «Ö» представлена 214 или 11010110 в двоичном формате.
Хотя расширенный ASCII удваивает набор символов стандартного ASCII, он не включает достаточно символов для поддержки всех языков.Например, для некоторых азиатских языков требуются тысячи символов. Поэтому другие кодировки символов, такие как Latin-1 (ISO-8859-1) и UTF-8, теперь используются чаще, чем ASCII для документов и веб-страниц. UTF-8 поддерживает более миллиона символов.
Обновлено: 27 апреля 2020 г.
TechTerms — Компьютерный словарь технических терминов
Эта страница содержит техническое определение ASCII. Он объясняет в компьютерной терминологии, что означает ASCII, и является одним из многих технических терминов в словаре TechTerms.
Все определения на веб-сайте TechTerms составлены так, чтобы быть технически точными, но также простыми для понимания. Если вы найдете это определение ASCII полезным, вы можете сослаться на него, используя приведенные выше ссылки для цитирования. Если вы считаете, что термин следует обновить или добавить в словарь TechTerms, отправьте электронное письмо в TechTerms!
Подпишитесь на информационный бюллетень TechTerms, чтобы получать избранные термины и тесты прямо в свой почтовый ящик. Вы можете получать электронную почту ежедневно или еженедельно.
Подписаться
Что такое кодовая книга? | Samhda9
Кодовая книга предоставляет информацию о структуре, содержании и макете файла данных.Пользователям настоятельно рекомендуется просмотреть кодовую книгу исследования перед загрузкой файла (ов) данных.
Хотя кодовые книги сильно различаются по качеству и количеству предоставляемой информации, типичная кодовая книга включает:
- Расположение и ширина столбцов для каждой переменной
- Определения различных типов записей
- Коды ответов для каждой переменной
- Коды, используемые для индикации отсутствия ответа и отсутствия данных
- Точные вопросы и шаблоны пропусков, использованные в опросе
- Другие указания на содержание и характеристики каждой переменной
Дополнительно кодовые книги могут также содержать:
- Частоты ответа
- Цели обследования
- Определения понятий
- Описание плана и методологии обследования
- Копия анкеты обследования
- Информация о сборе, обработке данных и качестве данных
Тело кодовой книги описывает содержимое файла данных.Для каждой переменной в файле данных обычно включаются следующие элементы:
- Имя переменной : указывает номер или имя переменной, присвоенное каждой переменной в сборе данных.
- Расположение столбца переменной : указывает начальное положение и ширину переменной. Если переменная относится к типу множественных ответов, то указанная ширина соответствует ширине одного ответа.
- Метка переменной : указывает сокращенное описание переменной (максимум 40 символов), которое может использоваться для идентификации переменной.В некоторых случаях расширенную версию имени переменной можно найти в списке описания переменных.
- Код отсутствующих данных : указывает значения и метки отсутствующих данных. Если «9» является отсутствующим значением, тогда в кодовой книге может быть указано «9 = отсутствующие данные». Другие примеры отсутствующих меток данных включают «Отказано», «Не знаю», «Пусто (нет ответа)» и «Законный пропуск».



 Позиционные системы счисления.
Позиционные системы счисления. Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.
Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами. Числа дают информацию о количестве предметов. Эта информация должна быть закодирована, представлена в какой-то системе счисления. Какой из известных способов выбрать, зависит от решаемой задачи.
Числа дают информацию о количестве предметов. Эта информация должна быть закодирована, представлена в какой-то системе счисления. Какой из известных способов выбрать, зависит от решаемой задачи. 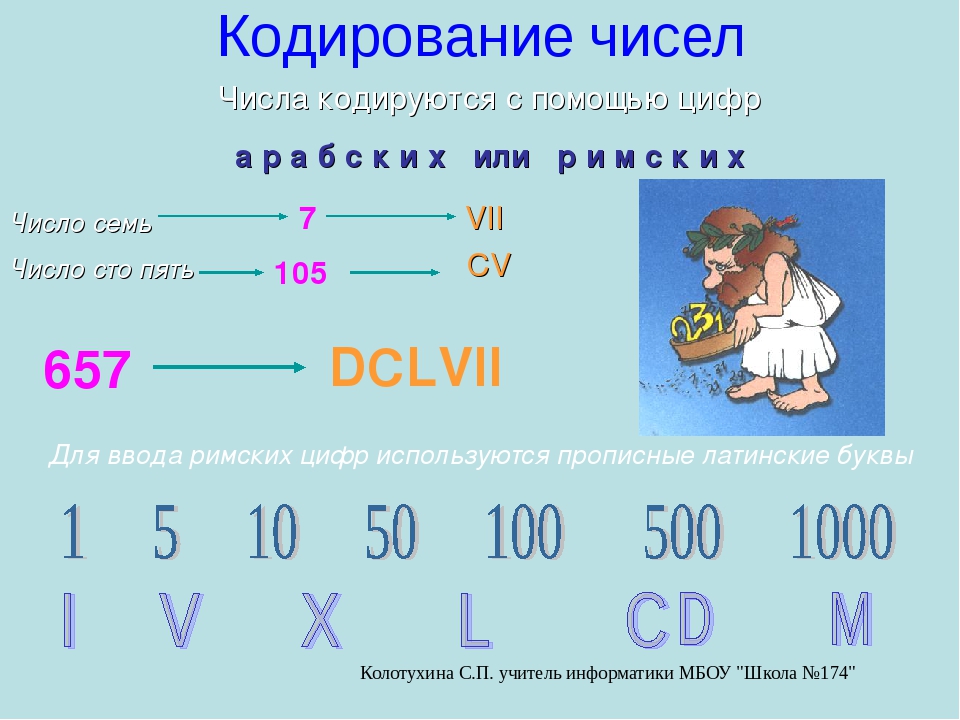 Последовательности из 0 и 1 называются двоичными кодами, а цифры 0 и 1 — битами (двоичными разрядами). Такое кодирование информации на компьютере называется двоичным кодированием. Таким образом, двоичное кодирование — это кодирование с минимально возможным числом элементарных символов, кодирование самыми простыми средствами. Тем оно и замечательно с теоретической точки зрения.
Последовательности из 0 и 1 называются двоичными кодами, а цифры 0 и 1 — битами (двоичными разрядами). Такое кодирование информации на компьютере называется двоичным кодированием. Таким образом, двоичное кодирование — это кодирование с минимально возможным числом элементарных символов, кодирование самыми простыми средствами. Тем оно и замечательно с теоретической точки зрения.  Для положительных чисел значение знакового разряда равно 0, а для отрицательных чисел — 1.
Для записи внутреннего представления целого отрицательного числа (-N) необходимо:
Для положительных чисел значение знакового разряда равно 0, а для отрицательных чисел — 1.
Для записи внутреннего представления целого отрицательного числа (-N) необходимо: 
 В 1964 году появились мощные IBM-360, в которых окончательно байт стал равен восьми битам. Последний восьмой бит был необходим для символов псевдографики.
Присвоение символу конкретного двоичного кода — это вопрос соглашения, которое фиксируется в кодовой таблице. К сожалению, существует пять различных кодировок русских букв, поэтому тексты, созданные в одной кодировке, не будут правильно отражаться в другой.
В 1964 году появились мощные IBM-360, в которых окончательно байт стал равен восьми битам. Последний восьмой бит был необходим для символов псевдографики.
Присвоение символу конкретного двоичного кода — это вопрос соглашения, которое фиксируется в кодовой таблице. К сожалению, существует пять различных кодировок русских букв, поэтому тексты, созданные в одной кодировке, не будут правильно отражаться в другой. 


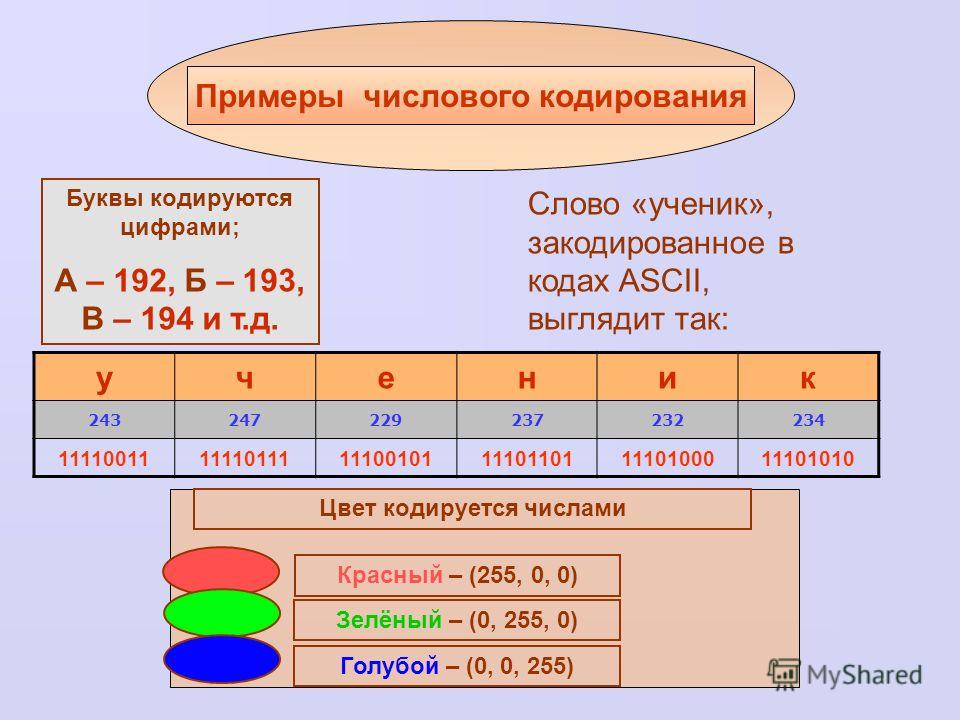 Программа драйвер клавиатуры и экрана по кодовой таблице определяет символ и создаёт его изображение на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде и программным способом преобразуются в изображения на экране.
Программа драйвер клавиатуры и экрана по кодовой таблице определяет символ и создаёт его изображение на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде и программным способом преобразуются в изображения на экране. Три бита позволяют закодировать 8 оттенков и т.д.
Три бита позволяют закодировать 8 оттенков и т.д. 

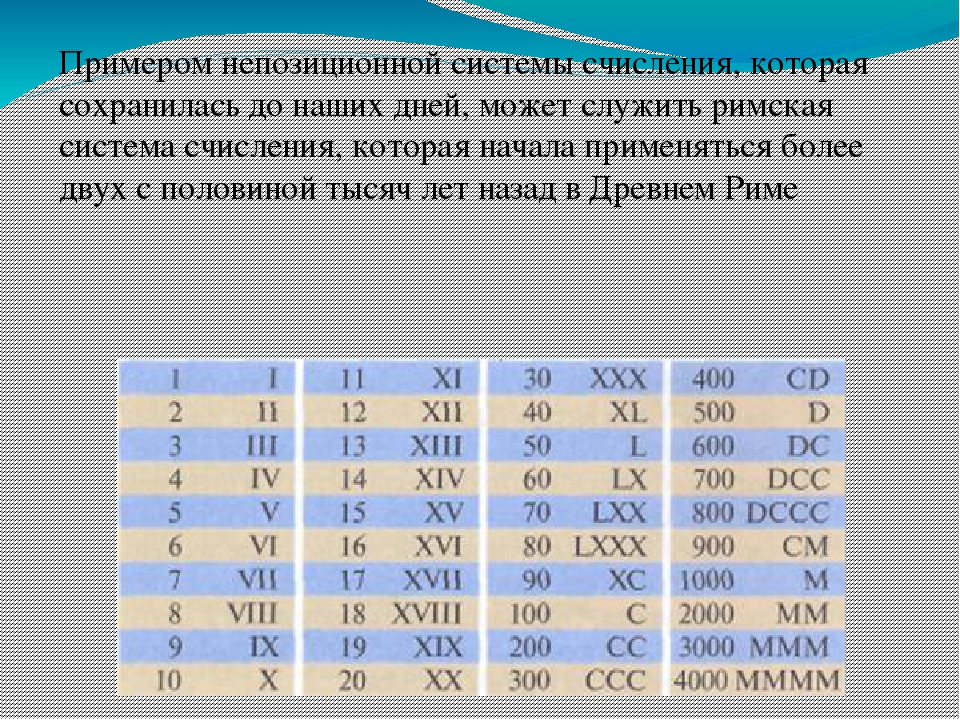 Если в середине 80-х годов обычный объём программ и данных составлял десятки и лишь иногда сотни килобайт, то в середине 90-х годов он стал составлять десятки мегабайт. Соответственно растёт объём оперативной памяти.
Если в середине 80-х годов обычный объём программ и данных составлял десятки и лишь иногда сотни килобайт, то в середине 90-х годов он стал составлять десятки мегабайт. Соответственно растёт объём оперативной памяти.