Вещественные числа — это… Что такое Вещественные числа?
Веще́ственные, или действи́тельные[1]числа — математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.
Множество вещественных чисел обозначается 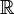 (Unicode: ℝ) и часто называется вещественной прямой.
(Unicode: ℝ) и часто называется вещественной прямой.
Относительно операций сложения и умножения вещественные числа образуют поле. Поле вещественных чисел является важнейшим объектом математического анализа.
Примеры
Определения
Существует несколько стандартных путей определения вещественных чисел:
Аксиоматическое определение
См. основную статью Аксиоматика вещественных чисел.
Множество вещественных чисел 
 , которое удовлетворяет следующим аксиомам:
, которое удовлетворяет следующим аксиомам:- Отношение
 является отношением линейного порядка:
является отношением линейного порядка: - Порядок согласован со структурой поля:
- Порядок на
 удовлетворяет условию полноты:
удовлетворяет условию полноты:
Примечания
Из свойства 3 следует, что у любого непустого ограниченного сверху множества 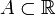 (то есть такого, что для всех x из A все
(то есть такого, что для всех x из A все 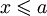
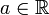 ) существует точная верхняя грань (минимальная из всех), то есть число
) существует точная верхняя грань (минимальная из всех), то есть число 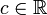 такое, что
такое, что- Для всех x из A все

- Если свойству (1) удовлетворяет также число
 , то
, то  .
.
Наличие точных верхних граней у ограниченных сверху множеств эквивалентно аксиоме полноты и часто заменяет её в аксиоматике поля 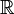
Любые два поля с отношением порядка, удовлетворяющим этим аксиомам, изоморфны, поэтому можно говорить, что существует единственное такое поле. (На самом деле, правильней говорить, что единственна структура полного упорядоченного поля, каждое поле, которое её имеет, служит моделью множества вещественных чисел, так как любые две модели изоморфны.)
Пополнение рациональных чисел
Вещественные числа 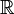 могут быть построены как пополнение множества рациональных чисел
могут быть построены как пополнение множества рациональных чисел 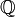 по отношению к обычной метрике
по отношению к обычной метрике 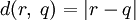
Более точно, рассмотрим все фундаментальные последовательности рациональных чисел {ri}. На таких последовательностях можно естественным образом ввести арифметические операции: {ri} + {qi} = {ri + qi} и 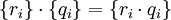 .
.
Две такие последовательности 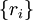 и
и 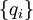 считаются эквивалентными
считаются эквивалентными 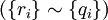 , если
, если 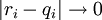
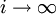 .
.Множество вещественных чисел можно определить как классы эквивалентности этих последовательностей.
Дедекиндовы сечения
См. основную статью Дедекиндово сечение.
Дедекиндово сечение — это разбиение множества рациональных чисел 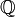 на два подмножества A и B такие, что:
на два подмножества A и B такие, что:
 для любых
для любых  и
и  ;
;- B не имеет минимального элемента.
Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.
Например, вещественному числу 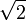 соответствует дедекиндово сечение, определяемое
соответствует дедекиндово сечение, определяемое 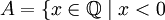 или
или 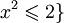 и
и 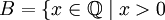 и x2 > 2}. Интуитивно, можно представить себе, что для того чтобы определить
и x2 > 2}. Интуитивно, можно представить себе, что для того чтобы определить 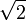 мы рассекли множество на две части: все числа, что левее
мы рассекли множество на две части: все числа, что левее 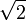 и все числа, что правее
и все числа, что правее 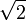 ; соотвеетственно,
; соотвеетственно, 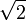 равно точной нижней грани множества B.
равно точной нижней грани множества B.
Бесконечные десятичные дроби
Такое задание, как правило, практикуется в школьной программе и во многом похоже на пополнение рациональных чисел.
Бесконечной десятичной дробью (со знаком) называется последовательность вида 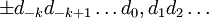 , где di являются десятичными цифрами, то есть
, где di являются десятичными цифрами, то есть 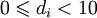 .
.
Две последовательности называются эквивалентными, если они либо совпадают, либо их различающиеся «хвосты» имеют вид 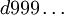 и
и 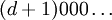 , где
, где 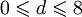 , либо если это «нулевые» последовательности (все di равны 0), отличающиеся только знаком.
, либо если это «нулевые» последовательности (все di равны 0), отличающиеся только знаком.
Вещественные числа определяются как классы эквивалентности десятичных дробей. Операции на десятичных дробях определяются позиционно подобно операциям над целыми числами в позиционных системах счисления.
Значение десятичной дроби формально задаётся суммой ряда 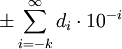 .
.
Счетность множества
TODO:
Примечания
- ↑ Традиционно в Петербурге (СПбГУ) принято название вещественные, а в Москве (МГУ) — действительные.
Ссылки
- Кириллов, А. А. Что такое число? // Выпуск 4-й серии «Современная математика для студентов». — М.: Физматлит, 1993.
- Понтрягин, Л. С. Обобщения чисел // Серия «Математическая библиотечка». — М.: Наука, 1965.
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
1.2. Вещественные числа и их свойства
Множество вещественных чисел является бесконечным. Оно состоит из рациональных и иррациональных чисел. Рациональным называется число вида p/q, где р и q — целые числа. Всякое вещественное число, не являющееся рациональным, называется иррациональным. Всякое рациональное число либо является целым, либо представляет собой конечную или периодическую бесконечную десятичную дробь. Например, рациональное число 1/9 можно представить в виде 0,11111…. Иррациональное число представляет собой бесконечную непериодическую десятичную дробь; примеры иррациональных чисел:
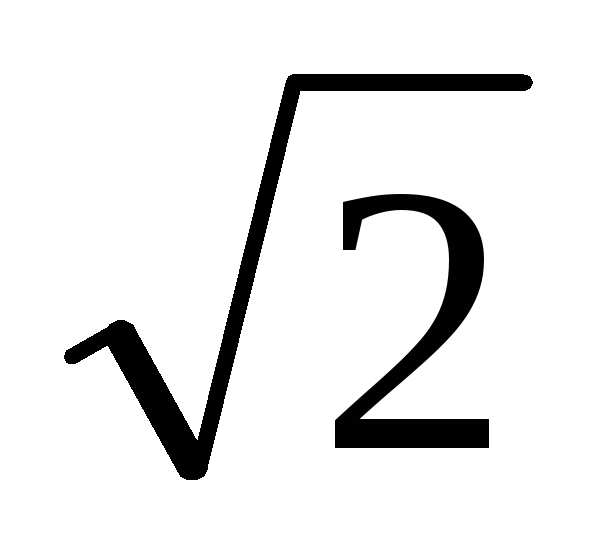 = 1,41421356…;
= 1,41421356…;  = 3,14159265….
= 3,14159265….
Сведения о вещественных числах могут быть кратко систематизированы в виде перечисления их свойств.
А. Сложение и умножение вещественных чисел
Для любой пары вещественных чисел а и b определены единственным образом два вещественных числа а + b и а ∙ b, называемые соответственно их суммой и произведением. Для любых чисел а,b и с имеют место следующие свойства.
1. a + b = b + а, а ∙ b = b ∙ а (переместительное свойство).
2. а + (b + с) = (а + b) + с, а ∙ (b ∙ с) = (а ∙ b) ∙ с (сочетательное свойство).
3. (а + b) ∙ с = а ∙ с + b ∙ с (распределительное свойство).
4. Существует единственное число 0, такое, что а + 0 = a для любого числа а.
5. Для любого числа а существует такое число (-а), что а + (-а) = 0.
6. Существует единственное число 1 ≠ 0, такое, что для любого числа а имеет место равенство
а ∙ 1 = a.
7. Для любого числа а ≠ 0 существует
такое число а-1,
что
а ∙ а-1 = 1.
Число а—1 обозначается также символом 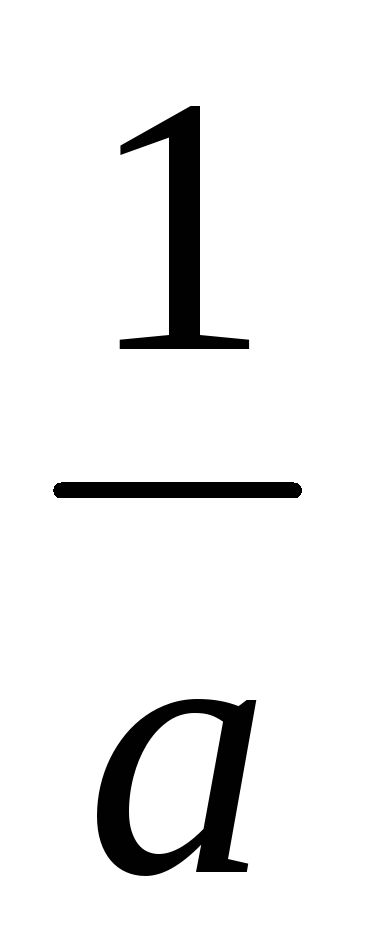 .
.
В. Сравнение вещественных чисел
Для любых двух вещественных чисел имеет место одно из трех соотношений: а = b (а равно b), а > b (а больше b) или а < b (а меньше b). Отношение равенства обладает свойством транзитивности: если а = b и b = с, то а = с.
Отношение «больше» обладает следующими свойствами.
8. Если а > b и b > с, то а > с.
9. Если а > b, то а + с > b + с.
10. Если а > 0 и b > 0, то а b > 0
Вместо соотношения а > b употребляют также b < а. Запись а ≥ b (b ≤ а) означает, что либо а = b, либо a > b. Соотношения со знаками >, <, ≥ и ≤ называютcя неравенствами, причем соотношения типа 8 < 10 — строгими неравенствами.
11. Любое вещественное число можно приблизить рациональными числами с произвольной точностью.
С. Непрерывность вещественных чисел.
12. Пусть
Х и
Y
— два множества вещественных чисел.
Тогда, если для любых чисел  и
и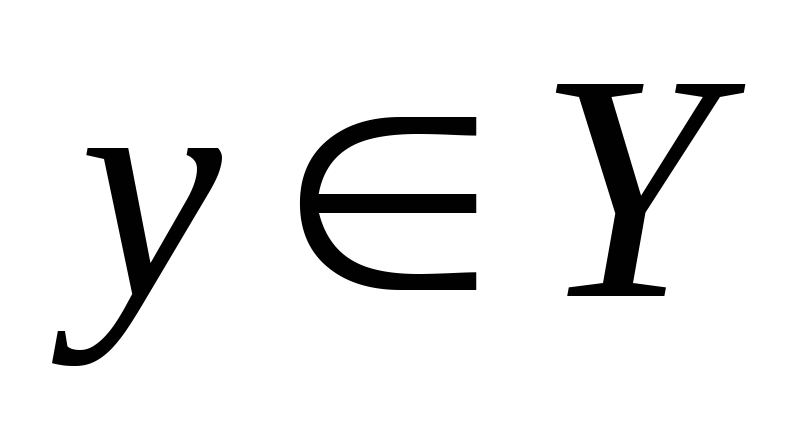 выполняется
неравенство х ≤ у,
то существует хотя бы одно число с,
такое, что для всех х и у выполняются
неравенства х ≤ с ≤ у.
выполняется
неравенство х ≤ у,
то существует хотя бы одно число с,
такое, что для всех х и у выполняются
неравенства х ≤ с ≤ у.
Отметим здесь, что свойством непрерывности обладает множество всех вещественных (действительных) чисел, но не обладает множество, состоящее только из рациональных чисел.
Таким образом, вещественные числа представляют собой множество элементов, обладающих свойствами А-С. Такое определение, из которого выводятся остальные свойства, называется аксиоматическим, а сами свойства А-С — аксиомами вещественных чисел.
studfile.net
ВЕЩЕСТВЕННЫЕ ЧИСЛА — это… Что такое ВЕЩЕСТВЕННЫЕ ЧИСЛА?
- ВЕЩЕСТВЕННЫЕ ЧИСЛА
то же, что действительные числа.
Большой энциклопедический политехнический словарь. 2004.
- ВЕЧНЫЙ ДВИГАТЕЛЬ
- ВЕЯЛКА
Смотреть что такое «ВЕЩЕСТВЕННЫЕ ЧИСЛА» в других словарях:
Вещественные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия
Числа с собственными именами — В этот список включены числа, имеющие собственные названия, не являющиеся стандартными сложносоставными названиями чисел. Именные названия степеней тысячи приводятся, только если у них есть иные названия. Содержание 1 Натуральные числа 1.1… … Википедия
Числа Кэли — Алгебра Кэли определённый тип гиперкомплексных чисел, 8 мерная алгебра над полем вещественных чисел. Обычно обозначается , поскольку её элементы (числа Кэли) называются иногда октонионами или октавами. Число Кэли это линейная комбинация… … Википедия
Числа в десятичной системе: от 10 до гуголплекса — Именные названия степеней тысячи в порядке возрастания Название Значение Американская система Европейская система тысяча 10³ 10³ миллион 106 106 миллиард 109 109 биллион 109 1012 триллион 1012 … Википедия
Числа Скьюза — Число Скьюза (англ. Skewes number) наименьшее целое число n такое, что , где количество простых чисел, не превосходящих , сдвинутый интегральный логарифм. Джон Литтлвуд в 1914 дал неконструктивное доказательство того … Википедия
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА — вещественные числа, общее назв. положит., отрицат. чисел и нуля. Д. ч. разделяются на рациональные, к рые представляются в виде дроби p/q, где р и q целые (q не равно 0), и иррациональные, к рые могут быть представлены в виде рацион. Д. ч. с… … Большой энциклопедический политехнический словарь
Комплексные числа — Запрос «Комплексные числа» перенаправляется сюда. Cм. также другие значения. Комплексные[1][2] числа расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма x + iy, где… … Википедия
Мнимые числа — Запрос «Комплексные числа» перенаправляется сюда. Cм. также другие значения. Комплексные[1][2] числа расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма x + iy, где… … Википедия
Конструктивные способы определения вещественного числа — При конструктивном подходе к определению вещественного числа вещественные числа строят, исходя из рациональных, которые считают заданными. Во всех трёх нижеизложенных способах за основу берутся рациональные числа и конструируются новые объекты,… … Википедия
Действительные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия
Книги
- Математический анализ. Вещественные числа и последовательности. Учебное пособие для академического бакалавриата, Садовничая И.В.. Учебное пособие посвящено темам&171;Вещественные числа&187;и&171;Предел числовой последовательности&187;. В первой главе рассматриваются элементы теории множеств, операции над ними,… Подробнее Купить за 466 грн (только Украина)
- Математический анализ. Вещественные числа и последовательности. Учебное пособие для СПО, Садовничая И.В.. Учебное пособие посвящено темам&171;Вещественные числа&187;и&171;Числовые последовательности&187;. В первой главе рассматриваются элементы теории множеств, операции над ними, эквивалентности… Подробнее Купить за 441 грн (только Украина)
- Математический анализ Вещественные числа и последовательности, Садовничая И., Фоменко Т., Хорошилова Е.. Учебное пособие посвящено темам «Вещественные числа» и «Числовые последовательности». В первой главе рассматриваются элементы теории множеств, операции над ними, эквивалентности и порядки,… Подробнее Купить за 361 руб
dic.academic.ru
определение, примеры, представления, координатная прямая
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?
Определение 1Действительные числа — это рациональные и иррациональные числа. Множество действительных чисел обозначается через R.
Данное определение можно записать иначе с учетом следующего:
- Рациональные числа можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
- Иррациональные числа представляют собой бесконечные непериодические десятичные дроби.
Действительные числа — числа, которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.
Действительные числа — это любые рациональные и иррациональные числа. Приведем примеры таких чисел: 0; 6; 458; 1863; 0,578; -38; 265; 0,145(3); log512.
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Еще одно название для действительных чисел — вещественные числа. Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
zaochnik.com
Вещественное число — это… Что такое Вещественное число?
- Вещественное число
- Вещественное число
- Вещественное число — в информатике — тип данных, содержащий числа, записанные с десятичной точкой и/или с десятичным порядком.
См. также: Типы данных
Финансовый словарь Финам.
.
- Вещание
- Вещное право
Смотреть что такое «Вещественное число» в других словарях:
вещественное число — действительное число — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы действительное число EN real number … Справочник технического переводчика
ВЕЩЕСТВЕННОЕ ЧИСЛО — то же, что действительное число … Большой Энциклопедический словарь
Вещественное число — Вещественное, или действительное число [1] математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение… … Википедия
вещественное число — то же, что действительное число. * * * ВЕЩЕСТВЕННОЕ ЧИСЛО ВЕЩЕСТВЕННОЕ ЧИСЛО, то же, что действительное число (см. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО) … Энциклопедический словарь
Вещественное число — то же, что Действительное число … Большая советская энциклопедия
ВЕЩЕСТВЕННОЕ ЧИСЛО — то же, что действительное число … Математическая энциклопедия
ВЕЩЕСТВЕННОЕ ЧИСЛО — то же, что действительное число … Естествознание. Энциклопедический словарь
ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО — вещественное число, положительное число, отрицательное число или нуль. Понятие Д. ч. возникло путем расширения понятия рационального числа. Необходимость этого расширения обусловлена как практическим использованием математики при выражении… … Математическая энциклопедия
Действительное число — вещественное число, любое положительное число, отрицательное число или нуль. Д. ч. разделяются на рациональные и иррациональные. Первые представимы как в виде рациональной дроби, т. е. дроби p/q, где р и q целые, q ≠ 0, так и в виде… … Большая советская энциклопедия
ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО — (вещественное число), любое положит., отрицат. число или нуль. Посредством Д. ч. выражаются результаты измерения всех физ. величин … Естествознание. Энциклопедический словарь
Книги
- Цепные дроби, В. И. Арнольд. Теория цепных дробей связана с теорией приближений вещественных чисел рациональными, с теорией динамических систем, а также со многими другими разделами математики. В брошюре рассказано о… Подробнее Купить за 118 грн (только Украина)
- Цепные дроби, Арнольд В.И.. Теория цепных дробей связана с теорией приближений вещественных чисел рациональными, с теорией динамических систем, а также со многими другими разделами математики. В брошюре рассказано о… Подробнее Купить за 91 руб
- Цепные дроби, В. И. Арнольд. Теория цепных дробей связана с теорией приближений вещественных чисел рациональными, с теорией динамических систем, а также со многими другими разделами математики. В брошюре рассказано о… Подробнее Купить за 88 руб
dic.academic.ru
ВЕЩЕСТВЕННОЕ ЧИСЛО — это… Что такое ВЕЩЕСТВЕННОЕ ЧИСЛО?
- ВЕШШЕЛЕНЬИ Миклош
- ВЕЩЕСТВО
Смотреть что такое «ВЕЩЕСТВЕННОЕ ЧИСЛО» в других словарях:
Вещественное число — в информатике тип данных, содержащий числа, записанные с десятичной точкой и/или с десятичным порядком. См. также: Типы данных Финансовый словарь Финам … Финансовый словарь
вещественное число — действительное число — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы действительное число EN real number … Справочник технического переводчика
Вещественное число — Вещественное, или действительное число [1] математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение… … Википедия
вещественное число — то же, что действительное число. * * * ВЕЩЕСТВЕННОЕ ЧИСЛО ВЕЩЕСТВЕННОЕ ЧИСЛО, то же, что действительное число (см. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО) … Энциклопедический словарь
Вещественное число — то же, что Действительное число … Большая советская энциклопедия
ВЕЩЕСТВЕННОЕ ЧИСЛО — то же, что действительное число … Математическая энциклопедия
ВЕЩЕСТВЕННОЕ ЧИСЛО — то же, что действительное число … Естествознание. Энциклопедический словарь
ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО — вещественное число, положительное число, отрицательное число или нуль. Понятие Д. ч. возникло путем расширения понятия рационального числа. Необходимость этого расширения обусловлена как практическим использованием математики при выражении… … Математическая энциклопедия
Действительное число — вещественное число, любое положительное число, отрицательное число или нуль. Д. ч. разделяются на рациональные и иррациональные. Первые представимы как в виде рациональной дроби, т. е. дроби p/q, где р и q целые, q ≠ 0, так и в виде… … Большая советская энциклопедия
ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО — (вещественное число), любое положит., отрицат. число или нуль. Посредством Д. ч. выражаются результаты измерения всех физ. величин … Естествознание. Энциклопедический словарь
Книги
- Цепные дроби, В. И. Арнольд. Теория цепных дробей связана с теорией приближений вещественных чисел рациональными, с теорией динамических систем, а также со многими другими разделами математики. В брошюре рассказано о… Подробнее Купить за 118 грн (только Украина)
- Цепные дроби, Арнольд В.И.. Теория цепных дробей связана с теорией приближений вещественных чисел рациональными, с теорией динамических систем, а также со многими другими разделами математики. В брошюре рассказано о… Подробнее Купить за 91 руб
- Цепные дроби, В. И. Арнольд. Теория цепных дробей связана с теорией приближений вещественных чисел рациональными, с теорией динамических систем, а также со многими другими разделами математики. В брошюре рассказано о… Подробнее Купить за 88 руб
dic.academic.ru
Значение словосочетания ВЕЩЕСТВЕННОЕ ЧИСЛО. Что такое ВЕЩЕСТВЕННОЕ ЧИСЛО?
Веще́ственное, или действи́тельное число (от лат. realis — действительный) — математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений, исследование поведения функций.Если натуральные числа возникли в процессе счёта, рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело ко множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.
Наглядно понятие вещественного числа можно представить при помощи числовой прямой. Если на прямой выбрать направление, начальную точку и единицу длины для измерения отрезков, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждой точке прямой можно поставить в соответствие некоторое вещественное число, и притом только одно. Вследствие этого соответствия термин «числовая прямая» обычно употребляется в качестве синонима множества вещественных чисел.
Понятие вещественного числа прошло долгий путь становления. Ещё в Древней Греции в школе Пифагора, которая в основу всего ставила целые числа и их отношения, было открыто существование несоизмеримых величин (несоизмеримость стороны и диагонали квадрата), то есть в современной терминологии — чисел, не являющихся рациональными. Вслед за этим Евдоксом Книдским была предпринята попытка построить общую теорию числа, включавшую несоизмеримые величины. После этого, на протяжении более двух тысяч лет, никто не ощущал необходимости в точном определении понятия вещественного числа, несмотря на постепенное расширение этого понятия. Лишь во второй половине XIX века, когда развитие математического анализа потребовало перестройки его основ на новом, более высоком уровне строгости, в работах К. Вейерштрасса, Р. Дедекинда, Г. Кантора, Э. Гейне, Ш. Мере была создана строгая теория вещественных чисел.
С точки зрения современной математики, множество вещественных чисел — непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле.
Множество вещественных чисел имеет стандартное обозначение — R («полужирное R»),
R
{\displaystyle \mathbb {R} }
или
R
{\displaystyle \mathbf {R} }
, Unicode U+211D: ℝ) (англ. blackboard bold «R») от лат. realis — действительный.
kartaslov.ru


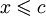
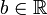 , то
, то 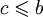 .
.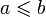 для любых
для любых 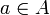 и
и 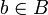 ;
;