Числа в памяти компьютера

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год | Числа в памяти компьютера

Основные темы параграфа:

— представление целых чисел;
— размер ячейки и диапазон значений чисел;
— особенности работы компьютера с целыми числами;
— представление вещественных чисел;
— особенности работы компьютера с вещественными числами.

Содержание урока

Представление целых чисел

Размер ячейки и диапазон значений чисел

Представление вещественных чисел

Вопросы и задания

Любая информация в памяти компьютера представляется в двоичном виде: последовательностью нулей и единиц. Исторически первым типом данных, с которыми стали работать компьютеры, были числа. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном итоге сводится к

обработке двоичных чисел — чисел, записываемых с помощью двух цифр, — 0 и 1.

Поэтому современные компьютерные технологии называют цифровыми технологиями.

В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера.

Представление целых чисел

Часть памяти, в которой хранится одно число, будем называть ячейкой. Минимальный размер ячейки, в которой может храниться целое число, — 8 битов, или 1 байт. Получим представление десятичного числа 25 в такой ячейке. Для этого нужно перевести число в двоичную систему счисления. Как это делается, вы уже знаете.

Результат перевода:

25₁₀ = 11001₂

.

Теперь осталось «вписать» его в восьмиразрядную ячейку (записать так называемое внутреннее представление числа). Делается это так:

00011001.

Число записывается «прижатым» к правому краю ячейки (в младших разрядах). Оставшиеся слева разряды (старшие) заполняются нулями.

Самый старший разряд — первый слева — хранит знак числа. Если число положительное, то в этом разряде ноль, если отрицательное — единица. Самому большому положительному целому числу соответствует следующий код:

01111111

Чему он равен в десятичной системе? Можно расписать это число в развернутой форме и вычислить выражение. Но можно решить задачу быстрее. Если к младшему разряду этого числа прибавить единицу, то получится число 10000000. В десятичной системе оно равно 2⁷ = 128. Значит:

01111111₂ = 128 — 1 = 127.

Максимальное целое положительное число, помещающееся в 8-разрядную ячейку, равно 127.

Теперь рассмотрим представление целых отрицательных чисел. Как, например, в 8-разрядной ячейке памяти будет представлено число -25?

Казалось бы, очевидным ответом является следующий: нужно в представлении числа 25 заменить старший разряд с 0 на 1. Но в компьютере все несколько сложнее.

Для представления отрицательных целых чисел используется дополнительный код.

Получить дополнительный код некоторого отрицательного числа -X можно по следующему алгоритму:

1) записать внутреннее представление соответствующего ему положительного числа +Х — это мы уже умеем;
2) записать обратный код полученного числа заменой во всех разрядах 0 на 1 и 1 на 0;
3) к полученному числу прибавить 1.

Определим по этим правилам внутреннее представление числа -25₁₀ в восьмиразрядной ячейке:

1)  00011001
2)  11100110
3)            +1

11100111 — это и есть представление числа -25.

В результате выполнении такого алгоритма единица в старшем разряде получается автоматически. Она и является признаком отрицательного значения.

Проверим полученный результат. Очевидно, что при сложении чисел +25 и -25 должен получиться ноль.

	0	0	0	1	1	0	0	1
+
	1	1	1	0	0	1	1	1
1	0	0	0	0	0	0	0	0

Единица в старшем разряде, получаемая при сложении, выходит за границу ячейки и исчезает. В ячейке остается нолъ.

Из этого примера теперь можно понять, почему представление отрицательного числа называется дополнительным кодом.

Представление восьмиразрядного отрицательного числа -X дополняет представление соответствующего положительного числа +Х до значения 2 ⁸.

xn—-7sbbfb7a7aej.xn--p1ai

Представление чисел в компьютере. Представление целых и вещественных чисел в памяти компьютера

Любому, кто хоть раз задумывался в жизни о том, чтобы стать «айтишником» или системным администратором, да и просто связать судьбу с вычислительной техникой, знание о том, как происходит представление чисел в памяти компьютера, абсолютно необходимо. Ведь именно на этом основываются языки программирования низкого уровня, такие как Assembler. Поэтому сегодня мы рассмотрим представление чисел в компьютере и их размещение в ячейках памяти.

Система счисления

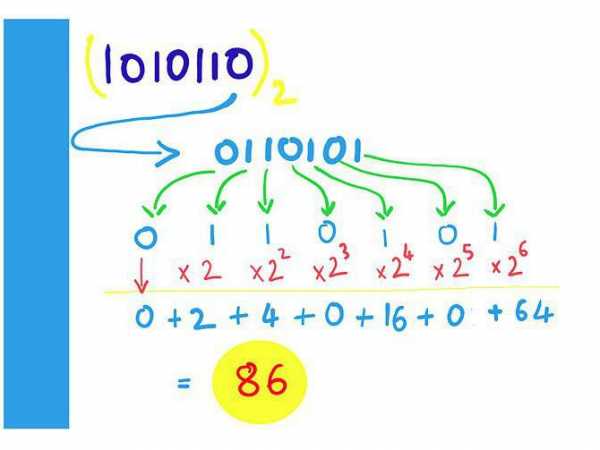
Если вы читаете данную статью, то, скорее всего, уже знаете об этом, но повторить стоит. Все данные в персональном компьютере хранятся в двоичной системе счисления. Это означает, что любое число необходимо представить в соответствующей форме, то есть состоящим из нулей и единиц.

Чтобы перевести привычные для нас десятичные числа к виду, понятному компьютеру, нужно воспользоваться описанным ниже алгоритмом. Существуют и специализированные калькуляторы.

Итак, для того чтобы перевести число в двоичную систему счисления, нужно взять выбранное нами значение и поделить его на 2. После этого мы получим результат и остаток (0 или 1). Результат опять делим 2 и запоминаем остаток. Данную процедуру нужно повторять до тех пор, пока в итоге также не окажется 0 или 1. Затем записываем конечное значение и остатки в обратном порядке, как мы их получали.

Именно так и происходит представление чисел в компьютере. Любое число записывается в двоичной форме, а потом занимает ячейку памяти.

Память

Как вам должно быть уже известно, минимальная единица измерения информации составляет 1 бит. Как мы уже выяснили, представление чисел в компьютере происходит в двоичном формате. Таким образом, каждый бит памяти будет занят одним значением – 1 или 0.

Для хранения больших чисел используются ячейки. Каждая такая единица содержит до 8 бит информации. Поэтому можно сделать вывод, что минимальное значение в каждом отрезке памяти может составлять 1 байт или быть восьмизначным двоичным числом.

Целые

Наконец мы подобрались к непосредственному размещению данных в компьютере. Как было уже сказано, первым делом процессор переводит информацию в двоичный формат, а только затем размещает в памяти.

Начнем мы с самого простого варианта, коим является представление целых чисел в компьютере. Память ПК отводит под этот процесс до смешного малое количество ячеек – всего одну. Таким образом, максимум в одном слоте могут быть значения от 0 до 11111111. Давайте переведём максимальное число в привычную нам форму записи.
Х = 1 × 2⁷ + 1 × 2⁶ + 1 × 2⁵ + 1 × 2⁴ + 1 × 2³ + 1 × 2² + 1 × 2¹ + 1 × 2⁰ = 1 × 2⁸ — 1 = 255.

Теперь мы видим, что в одной ячейке памяти может располагаться значение от 0 до 255. Однако это относится исключительно к целым неотрицательным числам. Если же компьютеру понадобится записать отрицательное значение, всё пройдет немного по-другому.

Отрицательные числа

Теперь давайте посмотрим, как происходит представление чисел в компьютере, если они являются отрицательными. Для размещения значения, которое меньше нуля, отводится две ячейки памяти, или 16 бит информации. При этом 15 уходят под само число, а первый (крайний левый) бит отдается под соответствующий знак.

Если цифра отрицательная, то записывается «1», если положительная, то «0». Для простоты запоминания можно провести такую аналогию: если знак есть, то ставим 1, если его нет, то ничего (0).

Оставшиеся 15 бит информации отводятся под число. Аналогично предыдущему случаю, в них можно поместить максимум пятнадцать единиц. Стоит отметить, что запись отрицательных и положительных чисел существенно отличается друг от друга.

Для того чтобы разместить в 2 ячейках памяти значение больше нуля или равное ему, используется так называемый прямой код. Данная операция производится так же, как и было описано, а максимальное А = 32766, если использовать десятичную систему счисления. Сразу хочется отметить, что в данном случае «0» относится к положительным.

Примеры

Представление целых чисел в памяти компьютера не является такой уж трудной задачей. Хотя она немного усложняется, если речь идет об отрицательном значении. Для записи числа, которое меньше нуля, используется дополнительный код.

Чтобы его получить, машина производит ряд вспомогательных операций.

1. Сначала записывается модуль отрицательного числа в двоичном счислении. То есть компьютер запоминает аналогичное, но положительное значение.
2. Затем проводится инвертирование каждого бита памяти. Для этого все единицы заменяются нулями и наоборот.
3. Прибавляем «1» к полученному результату. Это и будет дополнительный код.

Приведем наглядный пример. Пусть у нас есть число Х = — 131. Сначала получаем его модуль |Х|= 131. Затем переводим в двоичную систему и записываем в 16 ячеек. Получим Х = 0000000010000011. После инвертирования Х=1111111101111100. Добавляем к нему «1» и получаем обратный код Х=1111111101111101. Для записи в 16-битную ячейку памяти минимальным числом является Х = — (2¹⁵) = — 32767.

Длинные целые

Как видите, представление вещественных чисел в компьютере не так уж и сложно. Однако рассмотренного диапазона может не хватать для большинства операций. Поэтому, для того чтобы разместить большие числа, компьютер выделяет из памяти 4 ячейки, или 32 бита.

Процесс записи абсолютно не отличается от представленного выше. Так что мы просто приведем диапазон чисел, которые могут храниться в данном типе.

Х_мах=2 147 483 647.

Х_min=- 2 147 483 648.

Данных значений в большинстве случаев достаточно для того, чтобы записывать и проводить операции с данными.

Представление вещественных чисел в компьютере имеет свои преимущества и недостатки. С одной стороны, данная методика позволяет проще производить операции между целочисленными значениями, что значительно ускоряет работу процессора. С другой стороны, данного диапазона недостаточно для решения большинства задач экономики, физики, арифметики и других наук. Поэтому теперь мы рассмотрим очередную методику для сверхвеличин.

Плавающая запятая

Это последнее, что вам необходимо знать про представление чисел в компьютере. Поскольку при записи дробей возникает проблема определения положения запятой в них, для размещения подобных цифр в компьютере используется экспоненциальная форма.

Любое число может быть представлено в следующей форме Х = m * р^п. Где m – это мантисса числа, р – основание системы счисления и п – порядок числа.

Для стандартизации записи чисел с плавающей запятой используется следующее условие, согласно которому модуль мантиссы должен быть больше или равен 1/п и меньше 1.

Пусть нам дано число 666,66. Приведём его к экспоненциальной форме. Получится Х = 0,66666 * 10³. Р = 10 и п = 3.

На хранение значений с плавающей запятой обычно выделяется 4 или 8 байт (32 или 64 бита). В первом случае это называется числом обычной точности, а во втором – двойной точности.

Из 4 байт, выделенных под хранение цифр, 1 (8 разрядов) отдается под данные о порядке и его знаке, а 3 байта (24 разряда) уходят на хранение мантиссы и её знака по тем же принципам, что и для целочисленных значений. Зная это, мы можем провести нехитрые расчеты.

Максимальное значение п = 1111111²_{= 127¹⁰. Исходя из него, мы можем получить максимальный размер числа, которое может храниться в памяти компьютера. Х=2¹²⁷. Теперь мы можем вычислить максимально возможную мантиссу. Она будет равна 2²³ – 1 ≥ 2²³ = 2^{(10 × 2,3)} ≥ 1000^2,3 = 10^{(3 × 2,3)} ≥ 10⁷. В итоге, мы получили приближенное значение.}

Если теперь мы объединим оба расчета, то получим значение, которое может быть записано без потерь в 4 байта памяти. Оно будет равно Х = 1,701411 * 10³⁸. Остальные цифры были отброшены, поскольку именно такую точность позволяет иметь данный способ записи.

Двойная точность

Поскольку все вычисления были расписаны и объяснены в предыдущем пункте, здесь мы расскажем всё очень коротко. Для чисел с двойной точностью обычно выделяется 11 разрядов для порядка и его знака, а также 53 разряда для мантиссы.

П = 1111111111²_{= 1023¹⁰.}

М = 2⁵² -1 = 2^(10*5.2) = 1000^5.2 = 10^15.6. Округляем в большую сторону и получаем максимальное число Х = 2¹⁰²³ с точностью до «м».

Надеемся, информация про представление целых и вещественных чисел в компьютере, которую мы предоставили, пригодится вам в обучении и будет хоть немного понятнее, чем то, что обычно пишут в учебниках.

fb.ru

«Представление чисел в памяти компьютера»

План-конспект урока по информатике в 9 классе на тему «Представление чисел в памяти компьютера» (Слайд 1)

Цель: познакомить с представлением целых и вещественных чисел в памяти компьютера.

(Слайд 2)

Требования к знаниям и умениям (Слайд 3)

Учащиеся должны знать:

• представление целых чисел со знаком;

• представление целых чисел без знака;

• прямой код;

• обратный код;

• дополнительный код;

• мантиссу числа;

• представление вещественных чисел.

Учащиеся должны уметь:

• записывать целые числа с порядком;

• записывать прямой, обратный, дополнительный коды числа.

Программно-дидактическое оснащение: Сем., § 17, с. 100; демонстрация «Представление чисел в памяти компьютера»; проектор. (Слайд 4)

Ход урока

1. Организационный момент

2. Постановка целей урока

Сегодня на уроке мы найдем ответ на этот вопрос.

3. Актуализация знаний

1. Фронтальный опрос

1. Что такое системы счисления?

2. Что такое основание?

3. Назовите распространенные системы счисления.

4. Какой алфавит и основание имеет двоичная система счисления?

5. Какой алфавит и основание имеет десятичная система счисления?

6. Назовите правила перевода из десятичной в двоичную системы счисления.

7. Назовите правила перевода из двоичной в десятичную систему счисления.

8. Назовите правила сложения.

9. Назовите правила умножения.

2. Самостоятельная работа

Вариант 1

1. Переведите число в двоичную систему счисления: 102₁₀.

2. Переведите число из двоичной системы счисления в десятичную: 10111₂.

3. Вычислите:

11011₂ + 1011₂; 101₂ х 11₂.

Вариант 2

1. Переведите число в двоичную систему счисления: 99₁₀.

2. Переведите число из двоичной системы счисления в десятичную: 10101₂.

3. Вычислите:

101101₂ + 1101₂; 111₂

х 10₂.

Вариант 3

1. Переведите число в двоичную систему счисления: 87₁₀.

2. Переведите число из двоичной системы счисления в десятичную: 11011₂.

3. Вычислите:

10111₂+ 1110₂; 110₂ х 11₂.

Ответы:

Вариант 1 1. 1100110₂; 2. 23; 3. 100110₂; 1111₂.

Вариант 2. 1. 1100011₂; 2.21;3. 111010₂; 1110₂.

Вариант 3. 1. 1010111₂; 2. 27; 3. 10101₂; 10010₂.

4. Работа по теме урока

Любая информация в памяти компьютера представляется с помощью нулей и единиц, т. е. с помощью двоичной системы счисления. Первоначально компьютеры могли работать только с числами. Теперь это числа, тексты, графические объекты, видеоинформация, звук.

Работа с данными сводится любого типа к обработке двоичных чисел — чисел, записываемых с помощью двух цифр — 0 и 1.

В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера.

1. Представление целых чисел в компьютере (Слайд 5)

Целые числа могут представляться в компьютере со знаком или без знака.

Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 00000000₂ до 11111111₂, а в двубайтовом формате — от 00000000 00000000₂ до 11111111 11111111

2.

2. Диапазоны значений целых чисел без знака (Слайд 6)

(Объяснение сопровождается демонстрацией «Представление чисел в памяти компьютера»).

Формат числа в байтах

Запись с порядком

Обычная запись

1

0…2⁸ -1

0…255

2

0…2¹⁶ -1

0…65535

Пример.

Число72₁₀ = 1001000 в однобайтовом формате.

Число72₁₀ = 00000000001001000 в двубайтовом формате.

Целые числа со знаком (Слайд 7)обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» — единицей.

3. Диапазоны значений целых чисел со знаком (Слайд 8)

Формат числа в байтах

Запись с порядком

Обычная запись

1

— 2⁷… 2⁷ — 1

— 128…127

2

— 2¹⁵… 2¹⁵ — 1

— 32 768…32 767

4

— 2³¹… 2³¹ — 1

— 2 147 483 648…

2 147 483 647

Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины — семь разрядов.

(Слайд 9) В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код. Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.

(Слайд 10) Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде.

Пример.

Число 1₁₀= 1₂, число 127₁₀= 1111111₂.

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

1. Прямой код (Слайд 11) получается, если в знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины.

Пример.

Прямой код числа -1: 10000001. Прямой код числа -127: 11111111.

2. Обратный код (Слайд 12) получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями.

Пример.

Число: —1. Число: -127.

Код модуля числа: 0 0000001. Код модуля числа: 0 1111111.

Обратный код числа: 1 1111110. Обратный код числа: 1 0000000.

3. Дополнительный код (Слайд 13) получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.

Пример.

Дополнительный код числа -1: 11111111.

Дополнительный код числа -12: 11110100.

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.

(Слайд 14) Задание 1. Представьте число 45_]0 для записи числа в памяти компьютера.

Задание 2. Представьте число — 87₁₀ для записи числа в памяти компьютера.

4. Как представляются в компьютере вещественные числа (Слайд 15)

Система вещественных чисел в математических вычислениях предполагается непрерывной и бесконечной, т. е. не имеющей ограничений на диапазон и точность представления чисел. Однако в компьютерах числа хранятся в регистрах и ячейках памяти с ограниченным количеством разрядов. Вследствие этого система вещественных чисел, представимых в машине, является дискретной и конечной.

При написании вещественных чисел в программах вместо привычной запятой принято ставить точку.

Для отображения вещественных чисел, которые могут быть как очень маленькими, так и очень большими, используется форма записи чисел с порядком основания системы счисления.

(Объяснение сопровождается демонстрацией «Представление чисел в памяти компьютера».)

Пример. (Слайд 16)

Десятичное число 1,25 в этой форме можно представить так:

1,25 х 10° = 0,125 х 10¹ =0,0125 х 10² = … или так:

12,5 х 10^-1 = 125,0 х 10² = 1250,0 х 10^-3 = … .

Любое число N в системе счисления с основанием q можно записать в виде N = М х q^p, где М — множитель, содержащий все цифры числа (мантисса), а

infourok.ru

Числа в памяти компьютера

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год | Числа в памяти компьютера

Основные темы параграфа:

— представление целых чисел;
— размер ячейки и диапазон значений чисел;
— особенности работы компьютера с целыми числами;
— представление вещественных чисел;
— особенности работы компьютера с вещественными числами.

Содержание урока

Представление целых чисел

Размер ячейки и диапазон значений чисел

Представление вещественных чисел

Вопросы и задания

Размер ячейки и диапазон значений чисел

Наибольшее по модулю отрицательное значение в восьмиразрядной ячейке равно -2⁷ = -128. Его внутреннее представление: 10000000. Таким образом, диапазон представления целых чисел в восьмиразрядной ячейке следующий:

-128 ≤ X ≤ 127 или -2⁷ ≤ X ≤ 2⁷ — 1.

Восьмиразрядное представление целых чисел обеспечивает слишком узкий диапазон значений. Если требуется больший диапазон, нужно использовать ячейки большего размера. Для 16-разрядной ячейки диапазон значений будет следующим:

-2¹⁵ ≤ X ≤ 2¹⁵ — 1 или -32 768 ≤ X ≤ 32 767.

Теперь становится очевидной обобщенная формула для диапазона целых чисел в зависимости от разрядности N ячейки:

-2^N-1 ≤ Х ≤ 2^N-1 — 1.

Диапазон для 32-раз ряд ной ячейки получается достаточно большим:

-2³¹ ≤ X ≤ 2³¹ — 1 или -2 147 483 648 ≤ X ≤ 2 147 483 647.

Особенности работы компьютера с целыми числами

Выполняя на компьютере вычисления с целыми числами, нужно помнить об ограниченности допустимых значений.

Выход результатов вычислений за границы допустимого диапазона называется переполнением. Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.

xn—-7sbbfb7a7aej.xn--p1ai

Представление чисел в памяти компьютера.

Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера они должны располагаться в байтах – минимальных по размеру адресуемых ячейках памяти. В байте может содержаться произвольный код из 8 различных разрядов, и задача представления состоит в том, чтобы указать правила, как в одном или нескольких байтах записать число.

Один байт в памяти компьютера занимают целые числа от 0 до 255. Данные числа можно представить непосредственно в двоичном коде.

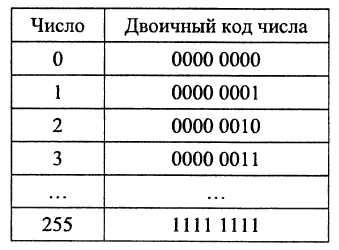
Для представления действительных чисел (как больших, так и малых) требуется больше одного байта. При этом бесконечные числа усекаются до определенного знака и в компьютерном представлении выступают как приближенные.

Для представления действительных чисел удобно использовать форму записи числа в виде произведения:

X=m·q^p,

где m– мантисса числа,

q– основание системы счисления,

p– целое число, называемое порядком.

Такой способ записи чисел называется представлением числа с плавающей точкой.

Действительные числа в компьютерах различных типов записываются по-разному, тем не менее существует несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру. Рассмотрим на примере числа, занимающего 4 байта (то есть 32 ячейки).

Первый бит двоичного представления используется для кодирования знака мантиссы (ноль интерпретируется как плюс, единица – как минус). Следующая группа бит кодирует порядок числа, а оставшиеся биты кодируют абсолютную величину мантиссы. Длина порядка и мантиссы фиксируются.

Вещественные числа в памяти компьютера, в зависимости от требуемой точности (количества разрядов мантиссы) и диапазона значений (количество разрядов порядка), занимают от 4 до 10 байтов. 4-х байтовое вещественное число имеет 23 разряда мантиссы (что соответствует точности числа 7-8 десятичных знаков) и 8 разрядов порядка (обеспечивающих диапазон значений 10^±38). Если вещественное число занимает 10 байт, то мантиссе отводится 65 разрядов, а порядку – 14 разрядов. Это обеспечивает точность 19-20 десятичных знаков мантиссы и диапазон значений 10^±4931.

Представление символьных и текстовых данных в двоичном коде.

С появлением ЭВМ возникла задача представления в цифровой форме нечисловых величин, и в первую очередь – символов, слов и текстов.

Для представления символов в числовой форме был предложен метод кодирования, получивший в дальнейшем широкое распространение и для других видов представления нечисловых данных.

В 1981 г. Институт стандартизации США принял стандарт кодовой таблицы, получившей название ASCII(AmericanStandardCodeofInformationInterchange– американский стандартный код информационного обмена). В последствии данный стандарт приобрел статус международного. Данная кодовая таблица рассчитана на объем памяти 1 байт, что позволяет закодировать 256 различных символов. Таблица состоит из 2-х частей: основной и расширенной. Основная часть (первые 127 символов) содержит: управляющие символы (коды с 1 по 31), арабские цифры, буквы латинского алфавита, знаки препинания, специальные символы (таблица 1).

Таблица 1.

Основная часть кода ASCII.

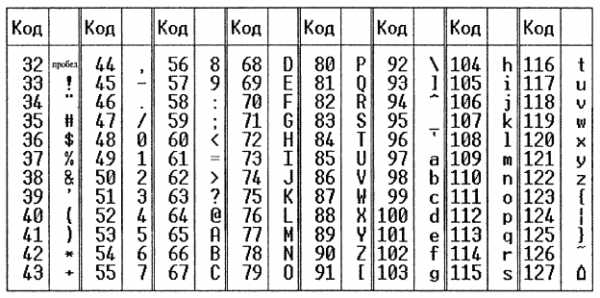
Расширенная часть (символы с кодами от 128 до 255) отделена для национальных алфавитов, символов псевдографики и некоторым специальным символам. Данная часть таблицы изменяется в зависимости от национального алфавита той страны, где она используется. 256 символов не позволяют одновременно закодировать несколько алфавитов в 1 таблице.

Поэтому в 1991 г. производители программных продуктов и организации, учреждающие стандарты, пришли к соглашению о выборе единого стандарта. Этот стандарт построен по 16 битной (или 2 байтной) схеме кодирования и получило название UNICODE. Данный стандарт позволяет закодировать 2¹⁶= 65536 символов, которых достаточно для кодирования основных национальных алфавитов в одной таблице.

Рекомендуемая литература:

1.Основы современных компьютерных технологий. Артамонов Б. Н. и другие – СПб, Корона-принт, 1998. – 446 с.

2.Основы защиты информации. Герасименко В. А. и другие – М.: Изд-во МИФИ, 1997. – 537 с.

3.Статистический анализ данных на компьютере. Тюрин Ю. Н. и другие – М.: Изд-во МИФИ, 1998. – 528 с.

4.Информатика. Соболь Б. В. и другие – Ростов н/Д: Феникс, 2007. – 446 с.

5.IBMPCдля пользователя (краткий курс). Фигурнов В. Э. – М.: ИНФРА-М, 2002. – 479 с.

7

studfile.net

Числа в памяти компьютера

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год | Числа в памяти компьютера

Основные темы параграфа:

— представление целых чисел;
— размер ячейки и диапазон значений чисел;
— особенности работы компьютера с целыми числами;
— представление вещественных чисел;
— особенности работы компьютера с вещественными числами.

Содержание урока

Представление целых чисел

Размер ячейки и диапазон значений чисел

Представление вещественных чисел

Вопросы и задания

Представление вещественных чисел

Целые и дробные числа в совокупности называются вещественными числами. В математике также используется термин «действительные числа».

Решение большинства математических задач сводится к вычислениям с вещественными числами.

Всякое вещественное число X можно записать в виде произведения мантиссы m и основания системы счисления в некоторой целой степени n, которую называют порядком:

X = m • р ⁿ.

Например, число 25,324 можно записать в таком виде: 0,25324 • 10². Здесь m = 0,25324 — мантисса, n = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.

Чаще всего для хранения вещественных чисел в памяти компьютера используется либо 32-разрядная, либо 64-разрядная ячейка. Первый вариант называется представлением с обычной точностью, второй — представлением с удвоенной точностью. В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядок. Здесь мы не будем подробно рассматривать правила представления вещественных чисел.

Отметим лишь основные следствия, вытекающие из этих правил, которые важно знать пользователю компьютера, занимающемуся математическими вычислениями.

Особенности работы компьютера с вещественными числами

1. Диапазон вещественных чисел ограничен. Но он значительно шире диапазона целых чисел в рассмотренном ранее способе и х представления. Например, при использовании 32-разрядной ячейки этот диапазон следующий:

-3,4 • 10³⁸ ≤ X ≤ 3,4 • 10³⁸.

2. Выход за диапазон (переполнение) — аварийная ситуация для процессора, который прерывает свою работу.

3. Результаты машинных вычислений о вещественными числами содержат погрешность. При использовании удвоенной точности эта погрешность уменьшаеися.

xn—-7sbbfb7a7aej.xn--p1ai

Вещественные числа. Вещественные числа в памяти компьютера.

Доброго времени суток уважаемый пользователь. На этой страничке мы поговорим на такие темы, как: Вещественные числа, Вещественные числа в памяти компьютера.

Предположим, в компьютер встроили устройство, кото­рое переводит числа из десятичной системы счисления в двоичную и обратно. Достаточно ли этого для представления чисел в памяти ЭВМ? Оказывается, нет. Мало научиться записывать числа, важно облегчить процесс автоматизированного выполнения арифметических действий над ними.

Вернемся к первым ЭВМ. Основным видом их «деятель­ности» были вычисления, но объём оперативной памяти и быстродействие процессора были невелики и инженерам приходилось придумывать разнообразные способы хранения и обработки чисел, чтобы даже сложные расчёты выполня­лись за разумное время.

Вещественные числа в памяти компьютера.

Операции над целыми числами выполнять проще, но на практике измерения в целых числах встречаются не так уж часто. Поэтому для целых чисел решено было отводить один или два байта. Один байт чаще всего отводился для всевозможных счётчиков, то есть для представления целых положитель­ных чисел.

Максимальным десятичным числом, которое можно было закодировать таким образом, было 255 в десятичной = 11111111 в двоичной = 2^8 — 1.

Для представления положительных и отрицательных це­лых чисел отводилось два байта (16 битов). В качестве при­знака, передающего знак числа, было выбрано значение старшего бита: 0 означал, что закодировано положительное число,  1 — отрицательное.

Максимальным десятичным числом, которое можно было закодировать таким образом, было 32767 в десятичной = 01111111 11111111 в двоичной =2^15. Целые без знака — это множество положитель­ных чисел в диапазоне [0, 2к-1], где к — это разряд­ность ячейки памяти, выделяемой под число. На­пример, если под целое число выделяется ячейка памяти размером в 16 разрядов (2 байта), то самое большое число будет таким: 0111111111111111. Например, десятичное число 255 после перевода в двоичную систему счисления и вписывания в 16-разрядную ячейку памяти будет иметь следующее внутреннее представление: 0000000011111111.

Отрицательные целые числа представляются в до­полнительном коде. Дополнительный код поло­жительного числа N — это такое его двоичное пред­ставление, которое при сложении с кодом числа N дает значение 2^к. Здесь к — количество разрядов в ячейке памяти. Например, дополнительный код числа 255 будет следующим: 1111111100000001.

Это и есть представление отрицательного числа -255. Сложим коды чисел 255 и —255:

Вычитание.

0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	255
1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	1	-255
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

1

Единичка в старшем разряде «выпала» из ячейки, поэтому сумма получилась равной нулю. Но так и должно быть: N + (— N) = 0. Процессор компьюте­ра операцию вычитания выполняет как сложение с дополнительным кодом вычитаемого числа. При этом переполнение ячейки (выход за предельные значе­ния) не вызывает прерывания выполнения программы. Это обстоятельство программист обязан знать и учитывать!

С вещественными числами дело обстояло немного слож­нее, поскольку надо было придумать способ, одинаковый для кодирования и больших, и маленьких чисел, то есть и миллион (1 000 000), и одну миллионную (0,000 001) хоте­лось бы кодировать посредством одного и того же алгорит­ма.

В соответствии с принципом позиционности любое деся­тичное число можно представить в виде произведения двух чисел, одно из которых меньше единицы, а другое представ­ляет собой некоторую степень десяти.

Такое представление чисел называется записью с плава­ющей точкой (запись 123,45 — запись с фиксированной точкой). В этой записи число имеет четыре характеристи­ки:

• Знак числа.
• Знак порядка.
• Порядок (степень числа 10).
• Мантисса (дробная часть числа).

При двоичном кодировании необходимо было все эти ха­рактеристики как-то отразить.

Максимальный порядок числа был равен 111111в двоичной = 63 в десятичной,следовательно, максимальным числом, которое можно было закодировать таким образом, было 10^63.

Формат представления вещественных чисел в ком­пьютере называется форматом с плавающей точ­кой. Вещественное число R представляется в виде произведения мантиссы т на основание системы счисления п в некоторой целой степени р, которую называют порядком: R = т х п^р.

Чтобы не было неоднозначности, договорились в ЭВМ использовать нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализованном представлении должна удовлетво­рять условию: 0,1п< т < 1я. Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. В некоторых случаях условие нормализации принимают следующим: 1 с индексом и < т < 10 с индексом п.

В памяти компьютера мантисса представляет­ся как целое число, содержащее только значащие цифры (0 целых и запятая не хранятся). Следова­тельно, внутреннее представление вещественного числа сводится к представлению пары целых чисел: мантиссы и порядка.

Было решено отводить под вещественные числа 4 байта (32 бита). Три младших байта отводилось под запись ман­тиссы, а старший байт включал в себя:

• Один (старший) бит — знак числа: 0 — положительное,
  1 — отрицательное.
• Один бит — знак порядка: 0-положительный, 1-отрицательный.
• Младшие 6 битов — порядок числа.

В разных типах компьютеров применяются различные варианты представления чисел в форме с плавающей точкой. Рассмотрим один из вариантов внутреннего представления вещественного числа в четырехбайтовой ячейке памяти.

В ячейке должна содержаться следующая инфор­мация о числе: знак числа, порядок и значащие циф­ры мантиссы.

Машинный порядок	Мантисса
1-й байт.	1-й, 2-й и 3-й байты.

В старшем бите 1-го байта хранится знак числа: 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит пер­вого байта содержат машинный порядок. В следую­щих трех байтах хранятся значащие цифры мантис­сы (24 разряда).

В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. Значит, машинный порядок изменяется в диапазоне от 0 до 127 (в десятичной системе счисления). Всего 128 значений. Порядок, очевидно, может быть как положительным, так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка: от —64 до 63.

Машинный порядок смещен относительно ма­тематического и имеет только положительные зна­чения. Смещение выбирается так, чтобы минимальному математическому значению порядка соответ­ствовал ноль. Связь между машинным порядком (Мр) и математическим (р) в рассматриваемом случае выражается формулой:
Мр = р + 64. Полученная формула записана в десятичной си­стеме. В двоичной системе формула имеет вид: МР = Р +10000000.

Для записи внутреннего представления веществен­ного числа необходимо:

• Перевести модуль данного числа в двоичную систему счисления с 24 значащими цифрами.
• Нормализовать двоичное число.
• Найти машинный порядок в двоичной системе счисления.
• Учитывая знак числа, выписать его представле­ние в четырехбайтовом машинном слове.

Диапазон вещественных чисел значительно шире диапазона целых чисел. Положительные и отрица­тельные числа расположены симметрично относи­тельно нуля. Следовательно, максимальное и мини­мальное числа равны между собой по модулю.
Наименьшее по абсолютной величине число рав­но нулю. Наибольшее по абсолютной величине чис­ло в форме с плавающей точкой — это число с самой большой мантиссой и самым большим порядком.

Если при вычислениях с вещественными числами результат выходит за пределы допустимого диапа­зона, то выполнение программы прерывается. Такое происходит, например, при делении на ноль, или на очень маленькое число, близкое к нулю.

Вещественные числа, разрядность мантиссы кото­рых превышает число разрядов, выделенных под мантиссу в ячейке памяти, представляются в компью­тере приближенно (с «обрезанной» мантиссой). Например, рациональное десятичное число 0,1 в компьютере будет представлено приближенно (ок­ругленно), поскольку в двоичной системе счисления его мантисса имеет бесконечное число цифр. След­ствием такой приближенности является погрешность машинных вычислений с вещественными числами.

Вычисления с вещественными числами компьютер выполняет приближенно. Погрешность таких вычис­лений называют погрешностью машинных ок­руглений.

Множество вещественных чисел, точно представимых в памяти компьютера в форме с плавающей точкой, является ограниченным и дискретным. Дискретность является следствием ограниченного числа разрядов мантиссы, о чем говорилось выше.

В настоящее время, когда быстродействие процессоров и объём оперативной памяти достаточно велики, а обычной разрядностью компьютеров становится 32 или 64 бита, уже нет жёстких требований к использованию экономных кодов для записи чисел.

На этом данную статью я заканчиваю, надеюсь, вы полностью разобрались с темами: Вещественные числа, Вещественные числа в памяти компьютера.

в нормализованном представлении должна удовлетво­рять условию: 0,1п

more-it.ru