Числа в памяти компьютера
Основные темы параграфа:
— представление целых чисел;
— размер ячейки и диапазон значений чисел;
— особенности работы компьютера с целыми числами;
— представление вещественных чисел;
— особенности работы компьютера с вещественными числами.
Содержание урока
Представление целых чисел
Размер ячейки и диапазон значений чисел
Представление вещественных чисел
Вопросы и задания
Любая информация в памяти компьютера представляется в двоичном виде: последовательностью нулей и единиц. Исторически первым типом данных, с которыми стали работать компьютеры, были числа. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном итоге сводится к обработке двоичных чисел — чисел, записываемых с помощью двух цифр, — 0 и 1.
 Поэтому современные компьютерные технологии называют цифровыми технологиями.
Поэтому современные компьютерные технологии называют цифровыми технологиями.
В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера.
Представление целых чисел
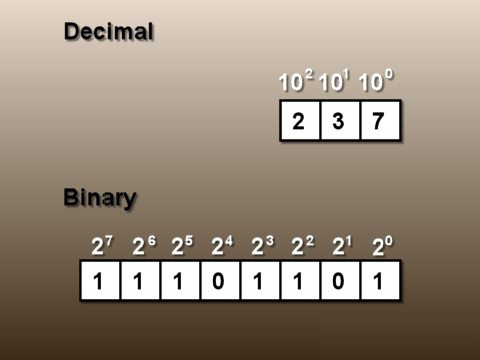
Часть памяти, в которой хранится одно число, будем называть ячейкой. Минимальный размер ячейки, в которой может храниться целое число, — 8 битов, или 1 байт. Получим представление десятичного числа 25 в такой ячейке. Для этого нужно перевести число в двоичную систему счисления. Как это делается, вы уже знаете.
Результат перевода:
2510 = 110012.
Теперь осталось «вписать» его в восьмиразрядную ячейку (записать так называемое внутреннее представление числа). Делается это так:
00011001.
Число записывается «прижатым» к правому краю ячейки (в младших разрядах). Оставшиеся слева разряды (старшие) заполняются нулями.
Самый старший разряд — первый слева — хранит знак числа. Если число положительное, то в этом разряде ноль, если отрицательное — единица. Самому большому положительному целому числу соответствует следующий код:
01111111
Чему он равен в десятичной системе? Можно расписать это число в развернутой форме и вычислить выражение. Но можно решить задачу быстрее. Если к младшему разряду этого числа прибавить единицу, то получится число 10000000. В десятичной системе оно равно 27 = 128. Значит:
011111112 = 128 — 1 = 127.
Максимальное целое положительное число, помещающееся в 8-разрядную ячейку, равно 127.
Теперь рассмотрим представление целых отрицательных чисел. Как, например, в 8-разрядной ячейке памяти будет представлено число -25?
Казалось бы, очевидным ответом является следующий: нужно в представлении числа 25 заменить старший разряд с 0 на 1. Но в компьютере все несколько сложнее.
Для представления отрицательных целых чисел используется дополнительный код.
Получить дополнительный код некоторого отрицательного числа -X можно по следующему алгоритму:
1) записать внутреннее представление соответствующего ему положительного числа +Х — это мы уже умеем;
2) записать обратный код полученного числа заменой во всех разрядах 0 на 1 и 1 на 0;
3) к полученному числу прибавить 1.
Определим по этим правилам внутреннее представление числа -2510 в восьмиразрядной ячейке:
1) 00011001
2) 11100110
3) +1
11100111 — это и есть представление числа -25.
В результате выполнении такого алгоритма единица в старшем разряде получается автоматически. Она и является признаком отрицательного значения.
Проверим полученный результат. Очевидно, что при сложении чисел +25 и -25 должен получиться ноль.
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |
| + | ||||||||
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Единица в старшем разряде, получаемая при сложении, выходит за границу ячейки и исчезает. В ячейке остается нолъ.
Из этого примера теперь можно понять, почему представление отрицательного числа называется дополнительным кодом.
 Представление восьмиразрядного отрицательного числа -X дополняет представление соответствующего положительного числа +Х до значения 2 8.
Представление восьмиразрядного отрицательного числа -X дополняет представление соответствующего положительного числа +Х до значения 2 8.
«Числа в памяти компьютера». 9-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- Образовательные:
- повторить понятие система счисления;
- повторить правила перевода из любой системы счисления в 10-ю и из 10-й системы счисления в любую;
- повторить правила перевода между 2-й, 8-й и 16-й системами счисления, используя метод триад и тетрад;
- дать представление о представлении положительных и отрицательных числах в памяти компьютера и особенностях работы с целыми числами;
- дать представление о разрядности ячейки памяти и диапазоне значений чисел;
- дать представление о представлении вещественных чисел в памяти компьютера и особенностях работы компьютера с вещественными числами.
- Развивающие:
- развивать внимание, логическое мышление, умение анализировать, сопоставлять, делать выводы.
- Воспитательные
- воспитание информационной культуры учащихся;
- прививать интерес к предмету информатика;
- прививать навыки самостоятельной работы;
- воспитание активности учащихся.
Формы организации учащихся на уроке: индивидуальная, фронтальная
Используемое оборудование: компьютеры, интерактивная доска
Программное обеспечение: презентация к уроку, проверочный тест.
ХОД УРОКА
I. Организационный момент
Приветствие, проверка письменного домашнего задания.
II. Актуализация полученных знаний
Учащиеся (несколько человек) проходят тест на компьютерах по теме: «Системы счисления». (Приложение 1)
Для остальных учащихся фронтальный опрос.
Вопросы для фронтального опроса:
– Что такое система счисления?
– Сколько цифр используются в 2-й, 8-й, 10-й, 16-й
системах счисления, перечислить какие.
– Перевести число 3458 в 10-ю систему
счисления.
– Перевести число 45110 в 16-ю систему
счисления.
– Перевод числа 10110011012 в 8-ю и 16-ю системы
счисления, используя триады и тетрады.
III. Изучение нового материала (Презентация)
Вся информация в памяти компьютера
представляется в двоичном виде, т.е. с помощью
нулей и единиц. Первоначально компьютеры могли
работать только с числами. Теперь это числа,
тексты, изображения, звук, видео. Работа с данными
любого типа сводится к обработке двоичных чисел
– чисел, записываемых с помощью двух цифр – 0 и 1.
Отсюда и название – «Цифровые технологии».
В компьютере различаются два типа числовых
величин: целые числа и вещественные числа.
Различаются способы представления чисел в
памяти компьютера.
- форма с фиксированной точкой (применяется к целым числам)
- форма с плавающей точкой (применяется к вещественным числам)
Представление целых чисел в форме с фиксированной запятой
Часть памяти компьютера, в которой хранится
одно число – ячейка. Минимальный размер ячейки,
где может храниться целое число – 8 бит или 1 байт.
Представим число 4210 в двоичной системе
счисления, а затем представим как будет
выглядеть это число в памяти компьютера.
4210 = 1010102.
Запишем полученное число в восьмиразрядную ячейку. Запись в ячейку производится с конца, то есть последняя цифра числа записывается в последний разряд ячейки, потом предпоследнюю цифру в предпоследний разряд ячейки и так далее пока не закончится число. Свободные разряды слева заполняются нулями.
Самый старший разряд (первый слева) – хранит знак числа. Если число положительное, то этот разряд равен 0, если отрицательное – 1.
Таким образом, самое большее положительное число, которое можно вписать в восьмиразрядную сетку имеет вид:
И это число 11111112 = 12710
Максимальное целое положительное число,
помещающееся в восьмиразрядную ячейку, равно 127.
Рассмотрим представление в памяти компьютера целых отрицательных чисел
Для представления целых отрицательных чисел
используется дополнительный код.
Дополнительный код числа можно получить, зная
следующий алгоритм:
- Записать внутреннее представление соответствующего ему положительного числа
- Записать обратный код полученного числа заменой во всех разрядах 0 на 1, и 1 на 0.
- К полученному числу прибавить 1.
Представим внутреннее представление числа – 4210 в восьмиразрядной ячейке: 4210 = 1010102
1) 00101010
2) 11010101 это обратный код
3) + 1
11010110 получили представление числа – 4210 в восьмиразрядной ячейке.
Старший разряд получил значение 1
автоматически. Единица в старшем разряде –
признак отрицательного числа.
Сложим числа 42 и – 42. Должны получить 0, проверим:
+ 00101010
11010110
100000000 получили число, старший разряд которого выходит за пределы восьмиразрядной ячейки, таким образом восьмиразрядная ячейка заполнена нулями, т.е. полученное при сложение число равно 0.
Представление восьмиразрядного отрицательного числа – Х дополняет представление соответствующего положительного числа Х до значения 28. Поэтому представление отрицательного целого числа называется дополнительным кодом.
Диапазон представления целых чисел в восьмиразрядной ячейке:
– 128 < X < 127 или –27 < Х < 27 – 1
Мы рассмотрели представление целых чисел на примере 8-ми разрядной ячейки, но бывают и 16-разрядные и 32-разрядные ячейки.
В 16-рядной ячейке можно получить числа диапазоном:
– 215 < X < 215 – 1 или – 32768 < X < 32767
В 32-разрядной ячейке можно получить числа диапазоном:
– 231 < X < 231 – 1 или – 2147483648 < X < 2147483647
Общая формула для диапазона целых чисел в зависимости от разрядности N ячейки:
– 2N–1 < X < 2N–1 – 1
Представление целых чисел в форме с плавающей запятой.
Вещественные числа это тоже, что и
действительные числа. Из курса математике вам
известно, что к действительным числам относятся
целые и дробные числа.
Всякое вещественное число X записывается в виде
произведения мантиссы m и основания
системы счисления p в некоторой целой степени n,
которую называют порядком:
X = m · pn
Например, число 25,324 = 0,25324 · 102
мантисса m = 0,25324, n = 2 – порядок. Порядок
указывает, на какое количество позиций и в каком
направлении должна сместится десятичная запятая
в мантиссе.
Чаще всего для хранения вещественных чисел в
памяти компьютера используется 32-разрядная или
64-разрядная ячейка. В первом случае это будет с
обычной точностью, во-втором случае с удвоенной
точностью. В ячейке хранятся два числа в двоичной
системе счисления: мантисса и порядка.
Диапазон вещественных чисел ограничен, но он
значительно шире, чем при представление целых
чисел в форме с фиксированной запятой.
Например, при использовании 32-разрядной ячейки
этот диапазон следующий:
–3,4 · 1038 < X < 3,4 · 1038
Результаты машинных вычислений с вещественными числами содержат погрешность. При удвоенной точности погрешность уменьшается. Выход из диапазона (переполнение) приводит к прерыванию работы процессора.
IV. Закрепление изученного материала
Выполнить самостоятельно задания №3(а,б) и №4(а,б) на странице учебника 105 с последующей проверкой
№3(а,б)
а) Записать внутреннее представление числа 32 в восьмиразрядную ячейку 3210 = 1000002
Значит внутреннее представление числа 32 в восьмиразрядную ячейку: 00100000
б) Записать внутреннее представление числа –32
в восьмиразрядную ячейку
32 имеет
представление
00100000
Обратный
код
11011111
+1
11100000
Значит внутреннее представление числа –32 в
восьмиразрядную ячейку: 11100000
№4(а,б)
а) Определить какому десятичному числу соответствует двоичный код 00010101 восьмиразрядного представления целого числа.
Видим, что первый разряд – 0, значит число положительное.
Переведём число 101012 в десятичную систему счисления:
1 · 24 + 0 · 23 + 1 · 22 + 0 · 21 + 1 · 20 = 16 + 4 + 1 = 2110
Значит двоичный код 00010101 восьмиразрядного представления целого числа 2110.
б) Определить какому десятичному числу соответствует двоичный код 11111110 восьмиразрядного представления целого числа.
Видим, что первый разряд – 1, значит число отрицательное. Для нахождения десятичного числа выполним алгоритм дополнительного кода в обратном порядке, а именно:
1) Вычтем из данного числа 1
11111110
– 1
11111101
2) Заменим 1 на 0 и 0 на 1
00000010
3) Переведём двоичное число 102 в десятичную систему счисления.
102 = 1 · 21 + 0 · 20 = 2
Таким образом, двоичный код 11111110 восьмиразрядного представления целого числа 210.
Задание: представить вещественное число
а) 0,0050589; б)1234,0456
в нормализованной форме с плавающей точкой в десятичной системе счисления.
Ответы:
а) 0,0050589 = 0,50589 · 10–2
б) 1234,0456 = 0,12340456 · 104
V. Итог урока
– Сегодня на уроке вы узнали, каким образом
хранятся числа в памяти компьютера. Как зависит
диапазон значений чисел от размера ячейки, в
которой хранится число.
Выставление оценок за урок (тест и задания №3, №4)
VI. Домашнее задание
Параграф 17, вопросы 1, 2, задания №3 (в,г), №4 (в,г)/
Числа в памяти компьютера
Основные темы параграфа:
— представление целых чисел;
— размер ячейки и диапазон значений чисел;
— особенности работы компьютера с целыми числами;
— представление вещественных чисел;
— особенности работы компьютера с вещественными числами.
Содержание урока
Представление целых чисел
Размер ячейки и диапазон значений чисел
Представление вещественных чисел
Вопросы и задания
Размер ячейки и диапазон значений чисел
Наибольшее по модулю отрицательное значение в восьмиразрядной ячейке равно -27 = -128. Его внутреннее представление: 10000000. Таким образом, диапазон представления целых чисел в восьмиразрядной ячейке следующий:
-128 ≤ X ≤ 127 или -27 ≤ X ≤ 27 — 1.
Восьмиразрядное представление целых чисел обеспечивает слишком узкий диапазон значений. Если требуется больший диапазон, нужно использовать ячейки большего размера. Для 16-разрядной ячейки диапазон значений будет следующим:
-215 ≤ X ≤ 215 — 1 или -32 768 ≤ X ≤ 32 767.
Теперь становится очевидной обобщенная формула для диапазона целых чисел в зависимости от разрядности N ячейки:
-2N-1 ≤ Х ≤ 2N-1 — 1.
Диапазон для 32-раз ряд ной ячейки получается достаточно большим:
-231 ≤ X ≤ 231 — 1 или -2 147 483 648 ≤ X ≤ 2 147 483 647.
Особенности работы компьютера с целыми числами
Выполняя на компьютере вычисления с целыми числами, нужно помнить об ограниченности допустимых значений.
Выход результатов вычислений за границы допустимого диапазона называется переполнением. Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.
§ 1.2. Представление чисел в компьютере
Ключевые слова:
• разряд
• беззнаковое представление целых чисел
• представление целых чисел со знаком
• представление вещественных чисел
1.2.1. Представление целых чисел
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).
Рис. 1.2. Ячейка памяти
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.
Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.
Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:
Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
Пример 1. Число 5310 = 1101012 в восьмиразрядном представлении имеет вид:
Это же число 53 в шестнадцати разрядах будет записано следующим образом:
При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.
В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/) размещён информационный модуль «Число и его компьютерный код». С помощью этого ресурса вы можете получить дополнительную информацию по изучаемой теме.
Для выполнения операций с отрицательными числами используется дополнительный код, позволяющий заменить операцию вычитания сложением. Узнать алгоритм образования дополнительного кода вы можете с помощью информационного модуля «Дополнительный код», размещённого на сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/).
1.2.2. Представление вещественных чисел
Любое вещественное число А может быть записано в экспоненциальной форме:
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Например, число 472 ООО ООО может быть представлено так: 4,72 • 108, 47,2 • 107, 472,0 • 106 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 • 109.
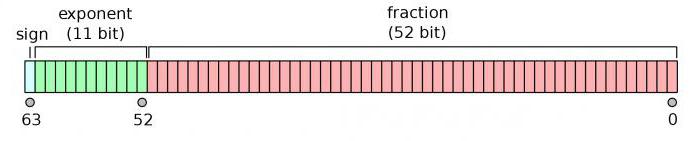
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:
Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
0,11111111111111111111111 • 101111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
САМОЕ ГЛАВНОЕ
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Как в памяти компьютера представляются целые положительные и отрицательные числа?
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
4. Представьте число 6310 в беззнаковом 8-разрядном формате.
5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100;
б) 00010101.
6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
7. Запишите следующие числа в естественной форме:
а) 0,3800456 • 102;
б) 0,245 • 10-3;
в) 1,256900Е+5;
г) 9,569120Е-3.
8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:
а) 217,93410;
б) 7532110;
в) 0,0010110.
10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
Электронное приложение к уроку

 |
 |
 |
||
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |

Cкачать материалы урока
Любому, кто хоть раз задумывался в жизни о том, чтобы стать «айтишником» или системным администратором, да и просто связать судьбу с вычислительной техникой, знание о том, как происходит представление чисел в памяти компьютера, абсолютно необходимо. Ведь именно на этом основываются языки программирования низкого уровня, такие как Assembler. Поэтому сегодня мы рассмотрим представление чисел в компьютере и их размещение в ячейках памяти.

Система счисления
Если вы читаете данную статью, то, скорее всего, уже знаете об этом, но повторить стоит. Все данные в персональном компьютере хранятся в двоичной системе счисления. Это означает, что любое число необходимо представить в соответствующей форме, то есть состоящим из нулей и единиц.
Чтобы перевести привычные для нас десятичные числа к виду, понятному компьютеру, нужно воспользоваться описанным ниже алгоритмом. Существуют и специализированные калькуляторы.
Итак, для того чтобы перевести число в двоичную систему счисления, нужно взять выбранное нами значение и поделить его на 2. После этого мы получим результат и остаток (0 или 1). Результат опять делим 2 и запоминаем остаток. Данную процедуру нужно повторять до тех пор, пока в итоге также не окажется 0 или 1. Затем записываем конечное значение и остатки в обратном порядке, как мы их получали.
Именно так и происходит представление чисел в компьютере. Любое число записывается в двоичной форме, а потом занимает ячейку памяти.

Память
Как вам должно быть уже известно, минимальная единица измерения информации составляет 1 бит. Как мы уже выяснили, представление чисел в компьютере происходит в двоичном формате. Таким образом, каждый бит памяти будет занят одним значением – 1 или 0.
Для хранения больших чисел используются ячейки. Каждая такая единица содержит до 8 бит информации. Поэтому можно сделать вывод, что минимальное значение в каждом отрезке памяти может составлять 1 байт или быть восьмизначным двоичным числом.
Целые
Наконец мы подобрались к непосредственному размещению данных в компьютере. Как было уже сказано, первым делом процессор переводит информацию в двоичный формат, а только затем размещает в памяти.
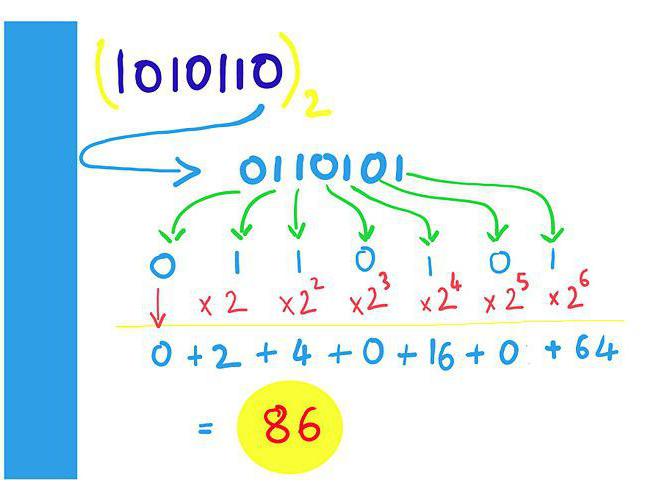
Начнем мы с самого простого варианта, коим является представление целых чисел в компьютере. Память ПК отводит под этот процесс до смешного малое количество ячеек – всего одну. Таким образом, максимум в одном слоте могут быть значения от 0 до 11111111. Давайте переведём максимальное число в привычную нам форму записи.
Х = 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 1 × 28 — 1 = 255.
Теперь мы видим, что в одной ячейке памяти может располагаться значение от 0 до 255. Однако это относится исключительно к целым неотрицательным числам. Если же компьютеру понадобится записать отрицательное значение, всё пройдет немного по-другому.

Отрицательные числа
Теперь давайте посмотрим, как происходит представление чисел в компьютере, если они являются отрицательными. Для размещения значения, которое меньше нуля, отводится две ячейки памяти, или 16 бит информации. При этом 15 уходят под само число, а первый (крайний левый) бит отдается под соответствующий знак.
Если цифра отрицательная, то записывается «1», если положительная, то «0». Для простоты запоминания можно провести такую аналогию: если знак есть, то ставим 1, если его нет, то ничего (0).
Оставшиеся 15 бит информации отводятся под число. Аналогично предыдущему случаю, в них можно поместить максимум пятнадцать единиц. Стоит отметить, что запись отрицательных и положительных чисел существенно отличается друг от друга.
Для того чтобы разместить в 2 ячейках памяти значение больше нуля или равное ему, используется так называемый прямой код. Данная операция производится так же, как и было описано, а максимальное А = 32766, если использовать десятичную систему счисления. Сразу хочется отметить, что в данном случае «0» относится к положительным.
Примеры
Представление целых чисел в памяти компьютера не является такой уж трудной задачей. Хотя она немного усложняется, если речь идет об отрицательном значении. Для записи числа, которое меньше нуля, используется дополнительный код.
Чтобы его получить, машина производит ряд вспомогательных операций.
- Сначала записывается модуль отрицательного числа в двоичном счислении. То есть компьютер запоминает аналогичное, но положительное значение.
- Затем проводится инвертирование каждого бита памяти. Для этого все единицы заменяются нулями и наоборот.
- Прибавляем «1» к полученному результату. Это и будет дополнительный код.
Приведем наглядный пример. Пусть у нас есть число Х = — 131. Сначала получаем его модуль |Х|= 131. Затем переводим в двоичную систему и записываем в 16 ячеек. Получим Х = 0000000010000011. После инвертирования Х=1111111101111100. Добавляем к нему «1» и получаем обратный код Х=1111111101111101. Для записи в 16-битную ячейку памяти минимальным числом является Х = — (215) = — 32767.
Длинные целые
Как видите, представление вещественных чисел в компьютере не так уж и сложно. Однако рассмотренного диапазона может не хватать для большинства операций. Поэтому, для того чтобы разместить большие числа, компьютер выделяет из памяти 4 ячейки, или 32 бита.
Процесс записи абсолютно не отличается от представленного выше. Так что мы просто приведем диапазон чисел, которые могут храниться в данном типе.
Хмах=2 147 483 647.
Хmin=- 2 147 483 648.
Данных значений в большинстве случаев достаточно для того, чтобы записывать и проводить операции с данными.
Представление вещественных чисел в компьютере имеет свои преимущества и недостатки. С одной стороны, данная методика позволяет проще производить операции между целочисленными значениями, что значительно ускоряет работу процессора. С другой стороны, данного диапазона недостаточно для решения большинства задач экономики, физики, арифметики и других наук. Поэтому теперь мы рассмотрим очередную методику для сверхвеличин.
Плавающая запятая
Это последнее, что вам необходимо знать про представление чисел в компьютере. Поскольку при записи дробей возникает проблема определения положения запятой в них, для размещения подобных цифр в компьютере используется экспоненциальная форма.
Любое число может быть представлено в следующей форме Х = m * рп. Где m – это мантисса числа, р – основание системы счисления и п – порядок числа.
Для стандартизации записи чисел с плавающей запятой используется следующее условие, согласно которому модуль мантиссы должен быть больше или равен 1/п и меньше 1.
Пусть нам дано число 666,66. Приведём его к экспоненциальной форме. Получится Х = 0,66666 * 103. Р = 10 и п = 3.
На хранение значений с плавающей запятой обычно выделяется 4 или 8 байт (32 или 64 бита). В первом случае это называется числом обычной точности, а во втором – двойной точности.
Из 4 байт, выделенных под хранение цифр, 1 (8 разрядов) отдается под данные о порядке и его знаке, а 3 байта (24 разряда) уходят на хранение мантиссы и её знака по тем же принципам, что и для целочисленных значений. Зная это, мы можем провести нехитрые расчеты.
Максимальное значение п = 11111112 = 12710. Исходя из него, мы можем получить максимальный размер числа, которое может храниться в памяти компьютера. Х=2127. Теперь мы можем вычислить максимально возможную мантиссу. Она будет равна 223 – 1 ≥ 223 = 2(10 × 2,3) ≥ 10002,3 = 10(3 × 2,3) ≥ 107. В итоге, мы получили приближенное значение.
Если теперь мы объединим оба расчета, то получим значение, которое может быть записано без потерь в 4 байта памяти. Оно будет равно Х = 1,701411 * 1038. Остальные цифры были отброшены, поскольку именно такую точность позволяет иметь данный способ записи.
Двойная точность
Поскольку все вычисления были расписаны и объяснены в предыдущем пункте, здесь мы расскажем всё очень коротко. Для чисел с двойной точностью обычно выделяется 11 разрядов для порядка и его знака, а также 53 разряда для мантиссы.
П = 11111111112 = 102310.
М = 252 -1 = 2(10*5.2) = 10005.2 = 1015.6. Округляем в большую сторону и получаем максимальное число Х = 21023 с точностью до «м».
Надеемся, информация про представление целых и вещественных чисел в компьютере, которую мы предоставили, пригодится вам в обучении и будет хоть немного понятнее, чем то, что обычно пишут в учебниках.
Числа в памяти компьютера
Основные темы параграфа:
— представление целых чисел;
— размер ячейки и диапазон значений чисел;
— особенности работы компьютера с целыми числами;
— представление вещественных чисел;
— особенности работы компьютера с вещественными числами.
Содержание урока
Представление целых чисел
Размер ячейки и диапазон значений чисел
Представление вещественных чисел
Вопросы и задания
Представление вещественных чисел
Целые и дробные числа в совокупности называются вещественными числами. В математике также используется термин «действительные числа».
Решение большинства математических задач сводится к вычислениям с вещественными числами.
Всякое вещественное число X можно записать в виде произведения мантиссы m и основания системы счисления в некоторой целой степени n, которую называют порядком:
X = m • р n.
Например, число 25,324 можно записать в таком виде: 0,25324 • 102. Здесь m = 0,25324 — мантисса, n = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.
Чаще всего для хранения вещественных чисел в памяти компьютера используется либо 32-разрядная, либо 64-разрядная ячейка. Первый вариант называется представлением с обычной точностью, второй — представлением с удвоенной точностью. В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядок. Здесь мы не будем подробно рассматривать правила представления вещественных чисел.
Отметим лишь основные следствия, вытекающие из этих правил, которые важно знать пользователю компьютера, занимающемуся математическими вычислениями.
Особенности работы компьютера с вещественными числами
1. Диапазон вещественных чисел ограничен. Но он значительно шире диапазона целых чисел в рассмотренном ранее способе и х представления. Например, при использовании 32-разрядной ячейки этот диапазон следующий:
-3,4 • 1038 ≤ X ≤ 3,4 • 1038.
2. Выход за диапазон (переполнение) — аварийная ситуация для процессора, который прерывает свою работу.
3. Результаты машинных вычислений о вещественными числами содержат погрешность. При использовании удвоенной точности эта погрешность уменьшаеися.
Числа в памяти компьютера
Цели урока:
I. Формирование предметной компетенции:
- Познавательные:
- дать представление о положительных и отрицательных числах в памяти компьютера;
- повторить понятия «система счисления», определение «бит»;
- повторить правила перевода чисел из двоичной СС в десятичную и наоборот.
- Практические:
- учить детей работать с инженерным калькулятором;
- учить с помощью алгоритма получать внутреннее представление отрицательных чисел.
II. Формирование метапредметных компетенций:
- Деятельностные компетенции (развивающие цели):
- познакомить с понятием «схема» и «рисунок»;
- определить отличие схемы от рисунка;
- развивать внимание, логическое мышление, умение сопоставлять и делать вывод, творческие умения.
- Социальные компетенции:
- работать в коллективе, слушать и слышать учителя, адекватно реагировать на ошибки, принимать решения.
III. Воспитательные цели:
- Вызвать интерес к изучению информатики как науке, изучающей хранение, передачу и обработку информации.
Тип урока: комбинированный урок – определяет особенности построения данного урока:
- Повторение ранее изученного материала.
- Актуализация.
- Целеполагание.
- Работа с определениями.
- Работа со схемой и рисунком.
- Практические задания на закрепление нового материала.
Оборудование, использованное учителем на уроке:
- раздаточный материал;
- АРМ учителя, проектор;
- ноутбуки.
Ход урока
Учитель: Здравствуйте, ребята. На доске представлено число и тема урока. Сегодня нам понадобятся рабочие тетради, ручки, ноутбуки.
А урок мы начнем с небольшого стихотворения (рисунок 1).
Рисунок 1
Скажите, пожалуйста, что в этом стихотворении необычного?
Ученик: Числа представлены в двоичной системе счисления.
Учитель: Что необходимо сделать, чтобы стихотворение стало понятным?
Ученик: Перевести числа из двоичной системы счисления в десятичную.
Учитель: Давайте вспомним определение системы счисления.
Ученик: Система счисления – способ записи чисел с помощью набора специальных знаков, называемых цифрами.
Рисунок 2
Учитель: Назовите основные системы счисления?
Ученик: Двоичная, десятичная, восьмеричная, шестнадцатеричная.
Рисунок 3
Учитель: Чтобы стихотворение стало понятным, переведем числа из двоичной системы счисления в десятичную (рисунок 1).
Читаем первую строчку: Ей было тысяча сто лет. Как мы переведем число из двоичной СС в десятичную. Вспомним правила перевода вместе. Вы работаете в тетрадях, а я у доски.
(Учитель на доске переводит первое число из двоичной системы счисления в десятичную.)
Итак, девочке было 12 лет.
11002 = 1 * 23 + 1 * 22 + 0 * 21 + 0 * 20 = 12
Рисунок 4>
А теперь каждый из вас самостоятельно переведет все остальные числа в десятичную систему счисления (у вас есть ровно 3 минуты).
(Ученики работают в тетрадях.)
Итак, проверяем:
В какой класс ходила девочка?
Ученик: В 5 класс.
1012 = 1 * 22 + 0 * 21 + 1 * 20 = 5
Рисунок 5
Учитель: Сколько книг она носила?
Ученик: 4 книги.
1002 = 1 * 22 = 4
Рисунок 6
Учитель: Сколько было ног, рук, ушей и глаз у девочки?
Ученик: Конечно по 2.
102 = 1 * 21 = 2
Рисунок 7
Учитель: Как вы уже поняли на практике, нам удобно пользоваться десятичной системой счисления. А компьютер работает с какими числами? (Правильно, с двоичными.)
Значит в компьютере числа представлены в виде 0 и 1.
Как принято называть нули и единицы?
Ученик: Эти два символа называются двоичными цифрами или битами.
Учитель: От каких двух английских слов произошло слово бит?
Ученик: Два символа 0 и 1 принято называть битами (от англ. binary digit – двоичный знак).
Рисунок 8
Учитель: Итак, мы с вами повторили перевод чисел из двоичной системы счисления в десятичную.
Цель дальнейшей работы: выяснить, как представлены положительные и отрицательные числа в памяти компьютера; научимся работать в инженерном калькуляторе; повторим правила перевода чисел из десятичной системы счисления в двоичную.
Итак, тема урока: «Числа в памяти компьютера».
Рисунок 9
Часть памяти, в которой хранится число, будем называть ячейкой памяти. Минимальная ячейка, которая может хранить число, состоит из 8 битов».
Минимальная ячейка памяти
для хранения – 8 битов
Рисунок 10
А сколько это будет в байтах?
Ученик: 1 байт.
Минимальная ячейка памяти
для хранения – 8 битов
8 бит = 1 байт
Рисунок 11
Учитель: Давайте представим число 25 в памяти компьютера. Что мы должны для этого сделать, как вы думаете?
Число 25
Рисунок 12
Ученик: Для этого нужно перевести число в двоичную СС и записать двоичный код числа в восьмиразрядную ячейку памяти.
Учитель: Хорошо, теперь на доске все вместе переведем число 25 из десятичной системы счисления в двоичную (учитель на доске вместе с ребятами переводят число 25).
Число 25
2510 = 110012
Рисунок 13
Хорошо, вспомнили. А переведем мы число 25 в двоичную систему счисления с помощью калькулятора, который есть у каждого на столе. Поработаем в парах. Все умеют пользоваться калькулятором?
Ученики: Да.
Учитель: Итак, у нас получилось двоичное число 11001. Хорошо, а теперь впишите это число в восьмиразрядную ячейку. Число записывается прижатым к правому краю ячейки. А оставшиеся слева ячейки заполняются нулями.
Число 25
Рисунок 14
Это и есть внутреннее представление положительных чисел в компьютере.
А одинаково ли выглядят в памяти компьютера отрицательные числа?
Ученик: Нет
Учитель: А мы сейчас с вами проверим: переведите с помощью калькулятора в двоичную СС число -25. Назовите двоичное число, которое у вас получилось.
Ученик: 11100111.
2510 = 000110012
-2510 = 000110012
Рисунок 15
Учитель: Значит, в памяти компьютера положительные и отрицательные числа записываются по-разному.
Как по внутреннему представлению числа понять положительное оно или отрицательное.
Ученик: По левому биту.
Учитель: Молодцы. Самый старший разряд – первый слева, хранит знак числа. Если там стоит 0, то это положительное число, если стоит 1 значит это отрицательное число.
Теперь вы можете ответить на вопрос: какое максимальное положительное двоичное число помещается в восьмибитовую ячейку?
Максимальное положительное число
в восьмибитовой ячейке
Рисунок 16
Ученик: 01111111.
Учитель: Правильно, а как это число будет выглядеть в десятичной системе счисления? Переведите на калькуляторе.
Ученик: Получилось 127.
Максимальное положительное число
в восьмибитовой ячейке
011111112 = 12710
Рисунок 17
Учитель: Мы с вами выяснили, что положительные и отрицательные числа представлены в памяти компьютера по-разному.
Посмотрите на экран, что вы видите на слайде?
Алгоритм получения дополнительного кода
отрицательных чисел на примере числа -25
Рисунок 18
Ученик: Схему.
Учитель: Хорошо. Чем отличается схема от рисунка?
Ученик: Схема – чертёж, изображающий устройство или взаимоотношение частей чего-либо. А рисунок – изображение на плоскости, созданное средствами графики.
Учитель: Хорошо, а что отражает данная схема?
Ученик: Алгоритм.
Учитель: Да, действительно перед вами алгоритм получения дополнительного кода отрицательных чисел на примере числа -25.
Алгоритм получения дополнительного кода
отрицательных чисел на примере числа -25
Рисунок 19
Определим по этим правилам внутреннее представление числа -25 в восьмиразрядной ячейки.
Внутренне представление числа 25 у нас уже есть 00011001.
Алгоритм получения дополнительного кода
отрицательных чисел на примере числа -25
Рисунок 20
Далее нам необходимо заменить все нули на единицы и наоборот 11100110
Алгоритм получения дополнительного кода
отрицательных чисел на примере числа -25
Рисунок 21
А теперь к полученному результату прибавляем 1 и получаем 11100111.
Алгоритм получения дополнительного кода
отрицательных чисел на примере числа -25
Рисунок 22
Это и есть внутренне представление отрицательного числа в памяти компьютера.
В результате выполнения такого алгоритма единица в левом бите получается автоматически. Она и является признаком отрицательного значения числа.
А теперь попробуйте самостоятельно, используя данный алгоритм, выполнить задания по карточкам, работаем в парах. У вас ровно 4 минуты. (Приложение 1).
Учитель: А теперь выполняем задания на повторение. Разбиваемся на группы, выполняем задания на карточках. Кто быстрее справится, та группа и победила (Приложение 2).
Эти все задания взяты из демонстрационных версий ЕГЭ по информатике. Как вы видите, задания достаточно легкие и очень интересные. Итак, проверяем.
(Учитель с учениками проверяют ответы.)
Итак, какую цель на уроке мы сегодня ставили?
Ученики: Выяснить, как представлены положительные и отрицательные числа в памяти компьютера; научимся работать в инженерном калькуляторе; повторим правила перевода чисел из десятичной системы счисления в двоичную.
Учитель: Мы достигли заданной цели?
Ученики: Да.
Учитель: Вы сегодня хорошо поработали на уроке. Особенно активными были…
- А теперь запишите, пожалуйста, домашнее задание:
- Параграф 17, стр. 100-105 прочитать.
- Вопросы и задания: стр. 105(1, 2, 3).
- Опредилить внутреннее представление чисел -17 и 17.
Память компьютера — это область временного хранения. Он содержит данные и инструкции, которые необходимы центральному процессору (ЦП). Перед запуском программы она загружается из памяти в память. Это позволяет ЦПУ прямой доступ к компьютерной программе. Память нужна на всех компьютерах.
Компьютер обычно представляет собой двоичное цифровое электронное устройство. Двоичный код означает, что он имеет только два состояния.Вкл или Выкл. Ноль или Один. В двоичном цифровом компьютере транзисторы используются для включения и выключения электричества. Память компьютера состоит из множества транзисторов.
Каждая настройка включения / выключения в памяти компьютера называется двоичной цифрой или битом. Группа из восьми битов называется байтом. Байт состоит из двух кусочков по четыре бита каждый. Информатики составили слова , бит и , байт . Слово , бит — это сокращение от , двоичная цифра . Он берет bi из двоичного кода и добавляет t из цифры.Коллекция битов была названа укус. Ученые-компьютерщики изменили орфографию до байт , чтобы избежать путаницы. Когда компьютерным ученым понадобилось слово для полбайта, они думали, что клев , как в половину укуса , было бы забавным словом для выбора. [1]
Байт памяти используется для хранения кода для представления символа, такого как число, буква или символ. Восемь битов могут хранить 256 различных кодов. Этого было достаточно, и байт стал фиксированным в восьми битах.Это позволяет использовать десять десятичных цифр, 26 букв нижнего регистра, 26 букв верхнего регистра и много символов. Ранние компьютеры использовали шесть бит на байт. Это дало им 64 разных кода. Эти компьютеры не имели строчных букв. [2]
Информатика должна была договориться о том, какой код будет представлять каждый символ. Большинство современных компьютеров используют ASCII, американский стандартный код для обмена информацией . В ASCII каждый код состоит из восьми битов — любая комбинация 0 и 1 — и образует один символ.Буква A обозначается кодом 01000001.
Чтобы учесть все разные символы на всех языках мира, современным компьютерам нужно более 256 разных символов. Другая система кодирования под названием Unicode позволяет использовать 1112 064 различных символов, используя от одного до четырех байтов для каждого символа.
ЦП компьютера может получить доступ к каждому отдельному байту. Он использует адрес для каждого байта. Адреса памяти компьютера начинаются с нуля и доходят до наибольшего числа, которое может использовать компьютер.Старые компьютеры были ограничены в объеме памяти, к которому они могли обращаться. 32-разрядные компьютеры могут адресовать до 4 ГБ памяти. Современные компьютеры используют 64 бита и могут адресовать до 18 446 744 073 709 551 616 байт = 16 эксабайт памяти.
Числа, которые используют компьютеры, могут стать очень большими. Для упрощения можно использовать единицу K (для килобайта) или Ki (для кибибайта). В памяти компьютера числа являются степенью двойки. Один кибибайт равен двум в степени 10, то есть 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 и записывается как 2 10 = 1024 байта.Например, 64 Кибибайта, записанные как 64 КБ или 64 КБ, памяти равны 65 536 байтам (1024 × 64 = 65 536). Для больших объемов памяти используются блоки мегабайт (МБ) или мегабайт (МиБ) и гигабайт (ГБ) или гибибайт (ГиБ). Один мегабайт памяти компьютера означает 2 20 байт или 1024 КБ, что составляет 1 048 576 байт. Один гибибайт означает 2 30 байт или 1024 МБ.
Числа кратны двум. Вот почему килобайт памяти составляет 1024 байта, а не 1000, как в случае с килограммом.Чтобы избежать этой путаницы, Международная электротехническая комиссия (МЭК) использует имена kibibyte, mebibyte и gibibyte для бинарных мощностей. Они используют килобайт, мегабайт и гигабайт для обозначения степеней 10. Объединенный совет по разработке электронных устройств (JEDEC) сохранил старые имена. Что еще хуже, размеры компьютерного хранилища, такого как жесткие диски (HDD), измеряются степенью десяти. Таким образом, диск на 500 ГБ имеет размер 500 x 1000 x 1000 x 1000 байт. Это намного меньше, чем 500 ГБ памяти, что составляет 500 х 1024 х 1024 х 1024.Большинство компьютерных ученых все еще используют старые имена и должны помнить, что единицы измерения различаются, когда речь идет о памяти и устройствах хранения.
Есть несколько программ и инструкций, которые всегда будут нужны компьютеру. Постоянное запоминающее устройство (ПЗУ) — это постоянное запоминающее устройство, которое используется для хранения этих важных управляющих программ и системного программного обеспечения для выполнения таких функций, как загрузка или запуск программ. ROM энергонезависимый. Это означает, что содержимое не теряется при отключении питания.Его содержимое записывается при сборке компьютера, но в современных компьютерах пользователь может изменять содержимое с помощью специального программного обеспечения.
Оперативная память (RAM) используется в качестве рабочей памяти компьютерной системы. Он временно хранит входные данные, промежуточные результаты, программы и другую информацию. Это может быть прочитано и / или написано. Обычно он нестабилен, что означает, что все данные будут потеряны при отключении питания. В большинстве случаев он снова загружается с жесткого диска, который используется в качестве хранилища данных.

Энергонезависимая память — это компьютерная память, которая хранит сохраненную информацию, когда она не включена.
Примеры энергонезависимой памяти включают в себя:
Иногда может относиться к памяти компьютера. Они всегда энергонезависимы.
примеров в том числе:
- ↑ «Определение клев». techtarget.com . TechTarget. Получено 5 декабря 2019 года.
откусывает метафору «съедобные данные», установленную с битами и байтами
- ↑ «Серия ICT / ICL 1900» (PDF).ourcomputerheritage.org. 16 декабря 2003 г. Получено 5 декабря 2019 г.
Память компьютера | Britannica
Первыми запоминающими устройствами были электромеханические переключатели или реле ( см. Компьютеры : первый компьютер) и электронные трубки ( см. Компьютеры : первые машины с хранимыми программами). В конце 40-х годов первые компьютеры с хранимыми программами использовали ультразвуковые волны в трубках ртути или заряды в специальных электронных трубках в качестве основной памяти. Последние были первой оперативной памятью (RAM). RAM содержит ячейки памяти, к которым можно обращаться напрямую для операций чтения и записи, в отличие от памяти с последовательным доступом, такой как магнитная лента, в которой каждая ячейка в последовательности должна быть доступна до тех пор, пока не будет найдена нужная ячейка.
Существует два основных типа полупроводниковой памяти. Статическая RAM (SRAM) состоит из триггеров, бистабильной схемы, состоящей из четырех-шести транзисторов. Как только триггер сохраняет бит, он сохраняет это значение до тех пор, пока в нем не будет сохранено противоположное значение. SRAM обеспечивает быстрый доступ к данным, но физически он относительно большой. Он используется в основном для небольших объемов памяти, называемых регистрами в центральном процессоре (ЦП) компьютера, и для быстрой «кэш-памяти». Динамическое ОЗУ (DRAM) хранит каждый бит в электрическом конденсаторе, а не в триггере, используя транзистор в качестве переключателя для зарядки или разрядки конденсатора.Поскольку в нем меньше электрических компонентов, ячейка памяти DRAM меньше SRAM. Однако доступ к его значению медленнее, и, поскольку конденсаторы постепенно теряют заряд, сохраненные значения должны заряжаться примерно 50 раз в секунду. Тем не менее, DRAM обычно используется для основной памяти, потому что чип такого же размера может содержать в несколько раз больше памяти DRAM, чем SRAM.
Ячейки памяти в оперативной памяти имеют адреса. Обычно ОЗУ организовано в «слова» длиной от 8 до 64 бит или от 1 до 8 байтов (8 бит = 1 байт).Размер слова, как правило, представляет собой количество битов, которые могут быть одновременно переданы между основной памятью и процессором. Каждое слово, и обычно каждый байт, имеет адрес. Микросхема памяти должна иметь дополнительные схемы декодирования, которые выбирают набор ячеек памяти, которые находятся по определенному адресу, и либо сохраняют значение по этому адресу, либо извлекают то, что хранится там. Основная память современного компьютера состоит из нескольких микросхем памяти, каждая из которых может содержать много мегабайт (миллионов байтов), и еще одна схема адресации выбирает соответствующую микросхему для каждого адреса.Кроме того, DRAM требует, чтобы схемы обнаруживали свои сохраненные значения и периодически обновляли их.
Основная память требует больше времени для доступа к данным, чем центральные процессоры, чтобы работать с ними. Например, доступ к памяти DRAM обычно занимает от 20 до 80 наносекунд (миллиардные доли секунды), но арифметические операции с ЦП могут занимать только наносекунду или меньше. Есть несколько способов обработки этого несоответствия. Процессоры имеют небольшое количество регистров, очень быструю SRAM, которая хранит текущие инструкции и данные, с которыми они работают.Кэш-память — это больший объем (до нескольких мегабайт) быстрой SRAM на чипе процессора. Данные и инструкции из основной памяти передаются в кэш, и поскольку программы часто демонстрируют «локальность ссылок», то есть они выполняют одну и ту же последовательность команд некоторое время в повторяющемся цикле и работают с наборами связанных данных, ссылки на память могут быть внесенным в быстрый кэш, как только значения будут скопированы в него из основной памяти.
Большая часть времени доступа к DRAM уходит на декодирование адреса для выбора соответствующих ячеек памяти.Свойство locality reference означает, что будет часто использоваться последовательность адресов памяти, а быстрый DRAM предназначен для ускорения доступа к последующим адресам после первого. Синхронный DRAM (SDRAM) и EDO (расширенный вывод данных) — два таких типа быстрой памяти.
Энергонезависимые полупроводниковые запоминающие устройства, в отличие от SRAM и DRAM, не теряют своего содержимого при отключении питания. Некоторые энергонезависимые запоминающие устройства, такие как постоянное запоминающее устройство (ПЗУ), невозможно перезаписать после изготовления или записи.Каждая ячейка памяти микросхемы ПЗУ имеет либо транзистор для 1 бита, либо ни одного для 0 бита. ПЗУ используются для программ, которые являются неотъемлемой частью работы компьютера, таких как программа начальной загрузки, которая запускает компьютер и загружает его операционную систему или BIOS (базовая система ввода / вывода), которая обращается к внешним устройствам в персональном компьютере (ПК).
EPROM (стираемое программируемое ПЗУ), EAROM (электрически изменяемое ПЗУ) и флэш-память — это типы энергонезависимой памяти, которые можно перезаписывать, хотя перезапись занимает гораздо больше времени, чем чтение.Таким образом, они используются в качестве памяти специального назначения, где запись редко требуется — например, при использовании для BIOS их можно изменить для исправления ошибок или обновления функций.
Как узнать, сколько слотов памяти в компьютере
Обновлено: 06/06/2020 от Computer Hope
Когда пользователь хочет добавить или обновить память (ОЗУ) на компьютере, он должен знать, сколько слотов памяти доступно. Следующий раздел поможет вам определить количество слотов памяти на вашем компьютере, а также их количество.
Windows Task Manager
Самое простое решение для пользователей Windows — открыть диспетчер задач Windows.
- Нажмите клавишу Windows, введите Диспетчер задач , а затем нажмите Введите .
- В открывшемся окне перейдите на вкладку Performance ( A ), затем выберите Память ( B ).
- В правом нижнем углу отображается количество слотов в используемых слотов: секция ( C ).
- Как видите, на этом компьютере всего четыре слота памяти, хотя в настоящее время используются только два.
Используйте утилиту CPU-Z
Еще один способ получить информацию о слотах памяти и сведениях об оперативной памяти, установленной в настоящее время на вашем компьютере, заключается в использовании бесплатной сторонней утилиты CPU-Z.
- Откройте интернет-браузер и посетите веб-сайт CPUID.
- В левой части экрана выберите свою операционную систему.
- На следующей странице выберите предпочитаемый язык.
- На следующем экране нажмите СКАЧАТЬ СЕЙЧАС! Кнопка
- После завершения загрузки установите ее из браузера и откройте программу.
- Перейдите на вкладку SPD в верхней части экрана, а затем нажмите стрелку вниз в разделе «Выбор слотов памяти» .
- Как видно на изображении выше, все слоты памяти (в данном случае четыре) перечислены в раскрывающемся меню.
Если вы выберете другой слот из выпадающего меню, CPU-Z сообщит вам дополнительную информацию об установленной ОЗУ или ничего, если слот не занят.
Изучите материнскую плату
Иногда лучший способ определить доступные слоты памяти — это открыть компьютер и проверить материнскую плату.Открытие компьютера — лучший вариант, если не удалось запустить диспетчер задач Windows или CPU-Z.
Если смотреть внутрь корпуса, материнская плата является основной большой печатной платой. На большинстве материнских плат слоты памяти расположены с обеих сторон процессора и напоминают то, что показано ниже.
Большинство компьютерных материнских плат имеют два, три или четыре слота памяти. Некоторые более дорогие материнские платы имеют целых восемь. На приведенном выше рисунке материнской платы нет модулей памяти, установленных в любом из трех слотов.
ЗаметкаЕсли на вашем компьютере нет свободных слотов памяти, и вы хотите обновить, вы должны удалить и заменить часть существующей памяти.
,ОЗУ системы | HowStuffWorks
Скорость оперативной памяти системы контролируется шириной шины , и скоростью шины . Ширина шины относится к числу битов, которые могут быть отправлены в ЦП одновременно, а скорость шины относится к числу раз, которые группа битов может отправлять каждую секунду. Цикл шины происходит каждый раз, когда данные перемещаются из памяти в ЦП. Например, 32-битная шина 100 МГц теоретически способна передавать 4 байта (32 бита, разделенных на 8 = 4 байта) данных в ЦП 100 миллионов раз в секунду, тогда как 16-битная шина 66 МГц может отправлять 2 байта данных 66 миллионов раз в секунду.Если вы посчитаете, вы обнаружите, что простое изменение ширины шины с 16 бит до 32 бит и скорости с 66 МГц до 100 МГц в нашем примере позволяет в три раза увеличить объем данных (400 миллионов байтов против 132 миллионов байтов). проходить к процессору каждую секунду.
Этот контент не совместим с этим устройством.
На самом деле ОЗУ обычно не работает с оптимальной скоростью. Задержка радикально меняет уравнение.Задержка относится к числу тактов, необходимых для считывания информации. Например, ОЗУ с частотой 100 МГц может отправлять бит за 0,00000001 секунды, но может потребоваться 0,00000005 секунд для запуска процесса чтения первого бита. Чтобы компенсировать задержку, процессоры используют специальную технику, называемую , пакетный режим .
Пакетный режимзависит от ожидания того, что данные, запрошенные ЦП, будут храниться в последовательных ячейках памяти .Контроллер памяти ожидает, что независимо от того, над чем работает ЦП, он будет продолжать поступать из этой же серии адресов памяти, поэтому он считывает несколько последовательных битов данных вместе. Это означает, что только первый бит подвергается полному эффекту задержки; чтение последовательных битов занимает значительно меньше времени. Пакетный режим памяти обычно выражается четырьмя числами, разделенными тире. Первое число сообщает вам количество тактов, необходимое для начала операции чтения; второе, третье и четвертое числа показывают, сколько циклов необходимо для считывания каждого последовательного бита в строке, также известного как словосочетания .Например: 5-1-1-1 говорит вам, что для чтения первого бита требуется пять циклов и один цикл для каждого бита после этого. Очевидно, что чем ниже эти цифры, тем выше производительность памяти.
Пакетный режимчасто используется в сочетании с конвейерной передачей , еще одним средством минимизации влияния задержки. Конвейерная обработка данных организует извлечение данных в своего рода сборочный процесс. Контроллер памяти одновременно считывает одно или несколько слов из памяти, отправляет текущее слово или слова в ЦП и записывает одно или несколько слов в ячейки памяти.При совместном использовании пакетный режим и конвейерная обработка могут значительно уменьшить задержку, вызванную задержкой.
Так почему бы вам не купить самую быструю и широкую память, какую только можно получить? Скорость и ширина шины памяти должны соответствовать системной шине. Вы можете использовать память, предназначенную для работы на частоте 100 МГц в системе 66 МГц, но она будет работать на частоте шины 66 МГц, поэтому это не дает никаких преимуществ, а 32-разрядная память не помещается на 16-разрядной. автобус.
Даже с широкой и быстрой шиной для передачи данных с карты памяти в ЦП все еще требуется больше времени, чем ЦП для фактической обработки данных.Вот тут и приходят кеши.
,
