Двоичное кодирование числовой информации в памяти компьютера
Цель урока: Познакомить учащихся с представлением числовой информации в памяти компьютера.
Задачи урока:
- образовательные: научить представлять целые числа в памяти компьютера, используя знания пройденного материала по информатике и математике, научить решать примеры по представлению целых чисел и выполнению операций над ними, используя ячейку памяти 1 байт, заполнить схему с алгоритмами действий над целыми числами;
- развивающие: развить познавательный интерес к предмету через сравнение выполнения операций над целыми числами человеком и компьютером;
- воспитательные: воспитать у учащихся информационную культуру для знания принципов работы электронных устройств, положительное отношение к учению, организованность при решении поставленной задачи.
Тип урока: изучение нового материала.
Форма урока: комбинированный.
План урока:
- Организационный момент.
- Актуализация знаний учащихся.
- Объяснение нового материала.
- Решение задач.
- Подведение итогов. Рефлексия.
- Домашнее задание.
Ход урока
1 этап – организационный момент
Здравствуйте, ребята!
Меня зовут …, и сегодня мы с вами будем работать вместе. (Положительный настрой)
2 этап – актуализация знаний
Продолжите, пожалуйста, фразы: (Слайд 1)
1. Основное устройство в кабинете информатики – это…
(Компьютер)
2. Для кодирования числовой информации в компьютере используется …
(Двоичный код, двоичная система счисления)
Опираясь на понятия: двоичный код, числовая информация, компьютер, попробуйте сформулировать тему. ( Слайд 2)
(Формулируют тему)
Тема урока: Двоичное кодирование числовой информации в памяти компьютера
Запишем тему в тетрадь.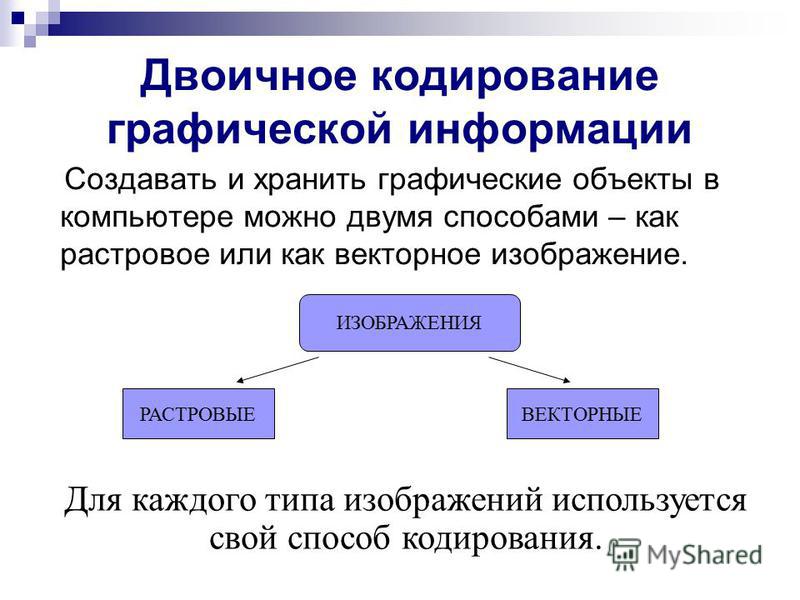
Исходя из темы урока, скажите, чем мы будем заниматься? (Слайд 3)
(Кодировать числовую информацию)
Цель урока: Познакомиться с двоичным кодирование числовой информации в памяти компьютера.
Задачи урока: (Слайд 4)
- Познакомиться с форматами представления чисел в компьютере.
- Научиться представлять целые числа в памяти компьютера.
- Научиться выполнять сложение двоичных кодов целых чисел.
- Закрепить алгоритмы представления целых чисел в памяти компьютера.
3 этап – объяснение нового материала
По какому принципу можно разделить следующие числа на две группы: -15; 127,5; 89; -27,4; -120; 34,7? (Слайд 5)
(Целые, дробные)
В информатике это целые числа и вещественные числа. С представлением целых чисел в памяти компьютера мы сегодня и познакомимся. Для этого мы возьмём ячейку 1 байт.
Для этого мы возьмём ячейку 1 байт.
У вас на партах есть схема. (Слайд 6) (Приложение 1) В течение урока мы будем её заполнять, для того, чтобы было удобно и понятно выполнять задания.
По какому принципу можно разделить целые числа на две группы: 18, -32, 47, -65, -72, 89? (Слайд 7)
(Положительные и отрицательные)
Впишите это в схему. (Слайд 8)
А как происходит представление целых чисел со знаком в ячейке памяти 1 байт? А 1 байт это сколько бит? (8)
Обратите внимание на слайд (Слайд 9): левый крайний разряд ячейки отводится под знак, остальные 7 разрядов – под число.
А какое количество чисел можно представить с помощью 7 разрядов? (N = 27 = 128)
Advertisement
Тогда положительные числа 0..127 – 7 разрядов + 0 в знаковом разряде, обозначающий знак +.
А отрицательные числа -1..-128 – 7 разрядов + 1 в знаковом разряде, обозначающий -.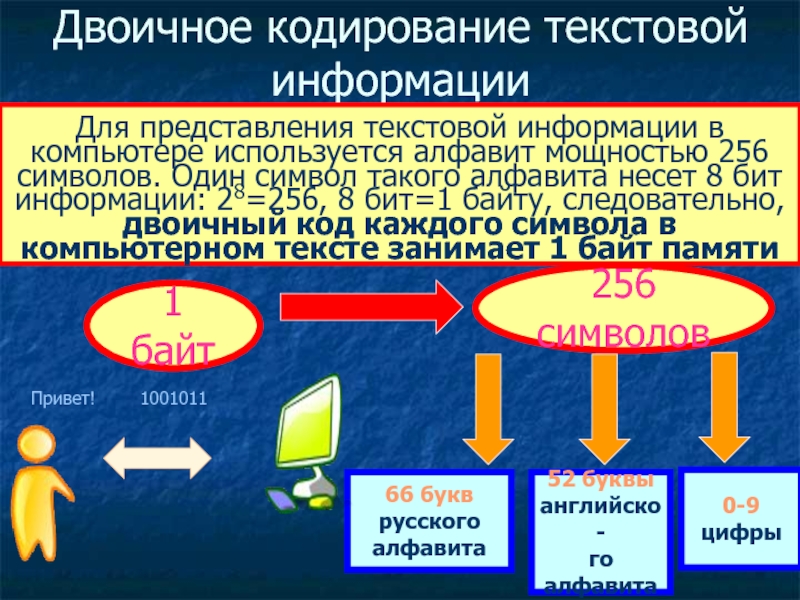
Запишем в схему числовые промежутки. (Слайд 10)
Посмотрите, пожалуйста, на пример. (Слайд 11)
Как представлено число 35 в ячейке памяти 1 байт? Что для этого надо сделать? (Перевести в 2 с/с и добавить незначащие нули до 8 разрядов.)
Запишем алгоритм представления целого положительного числа в памяти компьютера в схему. (
А теперь выполните задание 1 самостоятельно. (Слайд 13)
(Вызвать учащегося к доске)
Разберём представление отрицательных целых чисел в памяти компьютера. (Слайд 14)
Посмотрите, пожалуйста, на пример. Как представлено число -35 в ячейке памяти 1 байт?
Для этого нужно последовательно получить прямой, обратный и дополнительный код.
Запишем алгоритм (Слайд 15) представления целого отрицательного числа в памяти компьютера в схему. (Слайд 16)
А теперь выполните задание 2 самостоятельно. (Слайд 17)
(Слайд 17)
(Вызвать учащегося к доске)
Давайте сверим содержание схемы, которую вы получили и перейдём к выполнению действий. (Слайд 18)
4 этап – решение задач (закрепление)
Задание 3 (Слайд 19)
Найти сумму двоичных кодов и выполнить проверку в десятичной системе счисления. 2210+1710
(Вызвать к доске)
Задание 4 (Слайд 20)
Найти разность двоичных кодов и выполнить проверку в десятичной системе счисления. 2210-1710
(Вызвать к доске)
5 этап – подведение итогов, рефлексия (Слайд 21)
Вывод: Человек может складывать, вычитать, умножать, делить, возводить в степень, а компьютер – только складывать, используя дополнительный код, что увеличивает скорость работы компьютера. Причём так работает вся бытовая техника.
Рефлексия
Что узнали нового на уроке?
- Каким образом представляются положительные и отрицательные числа в памяти компьютера.
- Рассмотрели операцию сложения.)
На партах есть стикер. Нарисуйте на нём:
- 11, если всё понятно
- 01, если есть вопросы
- 00, если затрудняетесь ответить.
6 этап – домашнее задание (Слайд 22)
П. 4.1.4, № 4.11. По желанию попробуйте вычислить -22-17, решить примеры с карточек заданий.
Если остаётся время, раздать карточки с заданиями. (Приложение 2)
Конспект урока по информатике «Кодирование. Двоичный код»
План урока по информатике
Тема урока: Кодирование. Двоичный алфавит.
Цели: сформировать у обучающихся понимание процесса обмена информацией; показать различные виды кодирования информации; выявить преимущества двоичного кодирования различных видов информации.
Тип урока: урок-лекция.
Обучающиеся должны знать:
-что такое «код», «кодирование», «двоичное кодирование», бит;
-почему в вычислительной технике используется двоичное кодирование информации;
-как кодируются различные виды информации в вычислительной технике.
Обучающиеся должны уметь:
— кодировать информацию;
— восстанавливать информацию по ее кодовому представлению.
Оборудование: компьютер, проектор.
Программно-дидактическое обеспечение: ПК, программа PowerPoint, презентация в PowerPoint, таблицы, схемы.
План урока.
1. Организационный момент.
2. Изучение новой темы.
3. Закрепление нового материала.
4. Подведение итогов урока.
5. Постановка домашнего задания.
Постановка домашнего задания.
Ход урока
Организационный момент.
Преподаватель: Здравствуйте, ребята. Сегодня мы с вами изучим новую тему «Кодирование. Двоичный алфавит».
Постановка целей урока
Каким образом информация добирается от источника информации до приемника?
Что означает код 1101101?
Как информация кодируется в компьютере? Почему именно так?
2. Изложение нового материала
Кодирование информации
Когда человек или какой-либо другой живой организм или какое-то устройство участвуют в информационном процессе, то все они представляют информацию в той или иной форме. При выполнении домашнего задания вы также представляли информацию в различных формах.
Пояснение: вернитесь к домашнему заданию прошлого урока и спросите детей, чем они руководствовались при выборе тех или иных форм представления информации.
Так вот, когда мы представляем информацию в разных формах или преобразуем ее из одной формы в другую, мы информацию кодируем.
Код — это система условных знаков для представления информации.
Кодирование — это операция преобразования символов или группы символов одного кода в символы или группы символов другого кода.
Человек кодирует информацию с помощью языка.
Язык — это знаковая форма представления информации.
Одну и ту же информацию можно кодировать разными способами.
КОМПЬЮТЕР — русский язык
-• • — • -••_ •• • •-• — Код Морзе
COMPUTER — английский язык
67 79 77 80 85 84 69 82 — код ASCII.
Обычно при кодировании информации используется средство кодирования — некоторая таблица, которая устанавливает соответствие между знаками разных кодов. Например, для кода Морзе есть специальная таблица, в которой указаны символы алфавита и их представление с помощью набора точек и тире.
Таблица азбуки Морзе.
| А . — | О — — — | Э . . — — . . |
Б — . . . | П . — — . | Ю . . — — |
В . — — | Р . — . | Я . — . — |
Г — — . | С . . . | 1 . — — — — |
Д — . . | Т — | 2 . |
Е . | У . . — | 3 . . . — — |
Ж . . . — | Ф . . — . | 4 . . . . — |
З — — . . | Х . . . . | 5 . . . . . |
И . . | Ц — . — . | 6 — . . . . |
К — . — | Ч — — — . | 7 — — . . . |
Л . — . . | Ш — — — — | 8 — — — . . |
М — — | Щ — — . — | 9 — — — — . |
Н — . | Ъ,Ь — . | 0 — — — — — |
Пояснение: таблицу азбуки Морзе подготовьте заранее и раздайте детям.
В процессе обмена информацией кроме кодирования информации происходит и ее декодирование.
Упражнение.
Девочка заменила каждую букву своего имени ее номером в алфавите. Получилось 141261. Как зовут девочку?
Огромное количество способов кодирования информации неизбежно привело пытливый ум человека к попыткам создать универсальный язык или азбуку для кодирования. Эта проблемы была достаточно успешно реализована лишь в отдельных областях техники, науки и культуры. Своя система кодирования информации существует и в вычислительной технике. Она называется двоичным кодированием. Всю информацию, с которой работает вычислительная техника, можно представить в виде последовательности всего двух знаков – 1 и 0. Эти два символа называются двоичными цифрами, по-английски — binary digit или сокращенно bit – бит.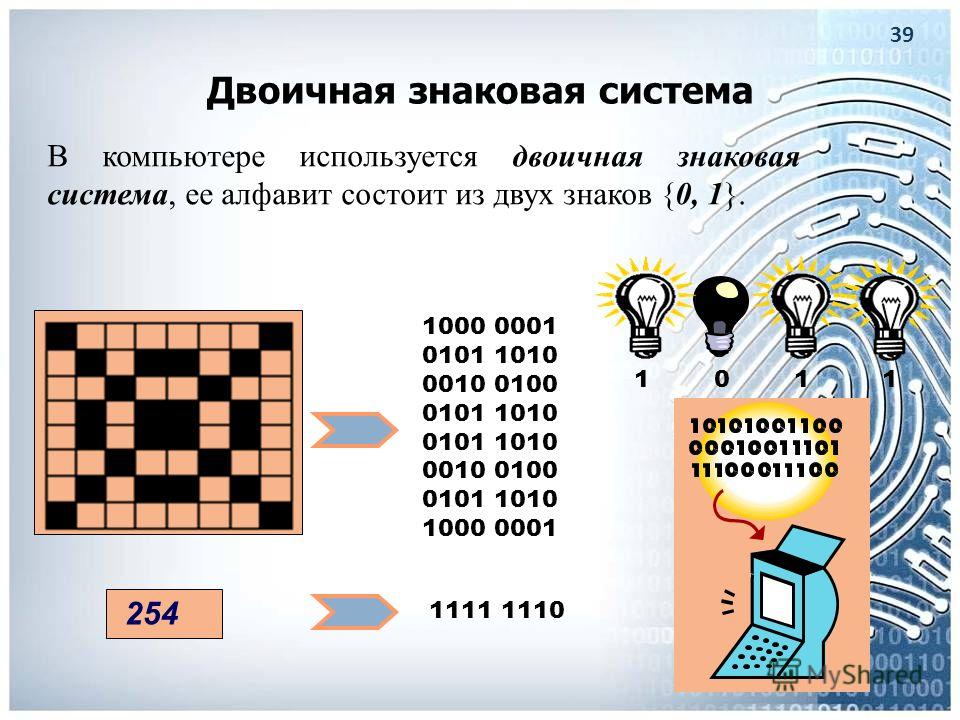
1 бит кодирует 2 понятия или сообщения (0 или 1).
2 бита – 4 разных сообщения (11 или 00 или 01 или 10).
3 бита – 8 разных сообщений.
4 бита – 16 сообщений и т.д.
Общая формула имеет вид: N=2m, где N – количество значений информации, m – количество бит.
Упражнение. Заполните таблицу.
Количество бит | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Количество сообщений |
Почему именно двоичное кодирование используется в вычислительной технике? Оказывается такой способ кодирования легко реализовать технически: 1 – есть сигнал, 0 – нет сигнала.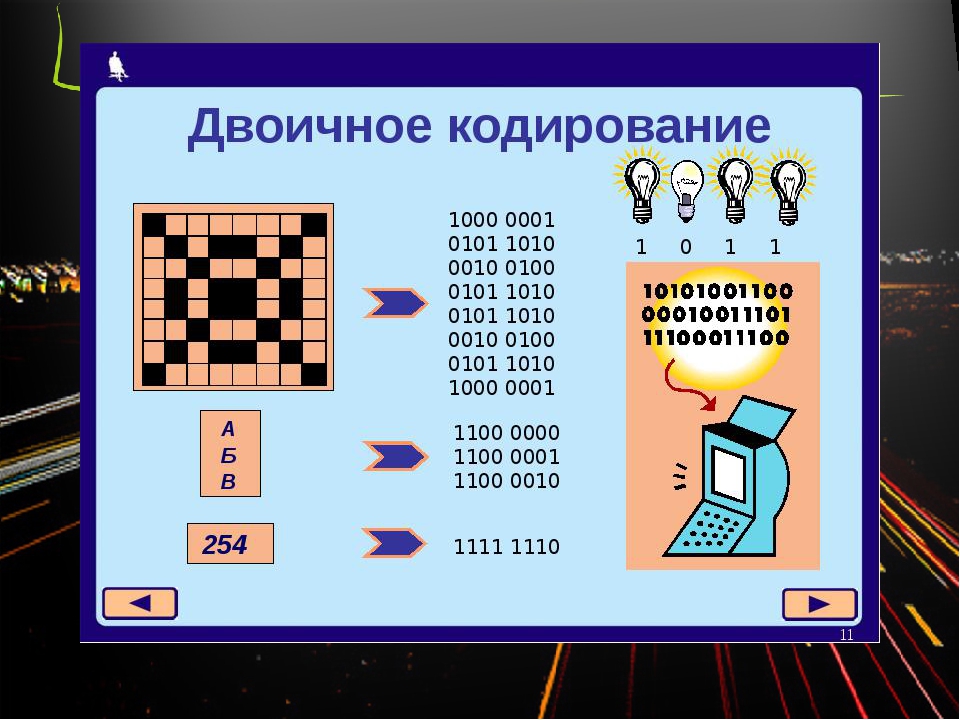 Для человека такой способ кодирования неудобен тем, что двоичные последовательности получаются достаточно длинными. Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.
Для человека такой способ кодирования неудобен тем, что двоичные последовательности получаются достаточно длинными. Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.
Закрепление нового материала.
Ответим на вопросы, поставленные в начале урока.
Каким образом информация добирается от источника информации до приемника?
Что означает код 1101101?
Как информация кодируется в компьютере? Почему именно так?
4. Итоги урока.
Сегодня на уроке мы с вами познакомились с понятиями «код», «кодирование», с различными формами кодировки информации, почему именно двоичное кодирование используется в компьютере.
Самые активные учащиеся получают оценки.
5. Домашнее задание.
С помощью азбуки Морзе закодировать свою фамилию и имя.
Подготовил:
Преподаватель информатики Куликов Андрей Карпович
Кодирование числовой информации
Введение
Если у вас возникли какие-либо вопросы при изучении темы «Кодирование числовой информации», то звоните мне и записывайтесь на первый репетиторский урок по информатике и ИКТ. На моих индивидуальных уроках мы с вами закроем текущие пробелы в ваших знаниях и прорешаем колоссальное количество всевозможных тематических упражнений.
Общие понятие о числовой информации
Думаю, что превалирующее число школьников и студентов знает фразу: «Математика – царица всех наук!». А как известно, математика очень интенсивно оперирует числами, цифрами и действиями над числами.
Первый счет появился много тысячелетий назад, так как даже в очень древние времена люди столкнулись с потребностью в счете. Его возникновение связано с желанием человека проинформировать своих соплеменников о количестве обнаруженных им объектов, предметов. По началу люди просто делили предметы по принципу один-много. То есть не было обозначения для двух, трех, десяти и более различных предметов. Их просто обозначали в количественном отношении как много.
По началу люди просто делили предметы по принципу один-много. То есть не было обозначения для двух, трех, десяти и более различных предметов. Их просто обозначали в количественном отношении как много.
Постепенно люди научились подключать к арифметическому счету пальцы на своих руках. С их помощью можно было считать до пяти, а если использовать обе руки, то до десяти различных предметов. Именно десятичная система счисления получило свое развитие на основе использования при счете пальцев рук.
Вернемся в настоящий временной континуум. Для современного человека знания, позволяющие считать предметы и записывать числа, являются обязательными. Арифметика изучается в школе с первого класса. Цифры, используя которые мы записываем числа, называются арабскими. Алфавит арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего десять различных цифр или состояний.
Числа можно классифицировать на две фундаментальные группы:
Каждое число из представленных групп может быть либо:
Примеры различных десятичных чисел:
-56 — целое отрицательное число;
12.
 78 — действительное положительное число;
78 — действительное положительное число;0.0 — действительное число, равное нулю;
12000 — целое положительное число.
Наша цель – понять, каким образом производится кодирование числовой информации, выраженной целыми или дробными числами, которые являются положительными, отрицательными или равными нулю. Другими словами, мы должны понять, как персональный компьютер хранит, обрабатывает, копирует числа на «своем» уровне.
Свойства числовой информации
Конечность. Информация, выраженная числовым значением, должна быть конечной. Процессор персонального компьютера не сможет обработать число, которое не является конечным или завершенным. То есть прежде чем приступить к кодированию числовой информации, процессор должен быть уверен, что данное значение записано полностью и не будет изменено пользователем.
Понятность. Если мы говорим о кодировании числовой информации, которая представлена десятичным числом, то необходимо, чтобы само число состояло из элементов, которые будут понятны исполнителю при кодировании.
 Исполнителем является, в строгом приближении, процессор персонального компьютера. Например, число 129 состоит из трех цифр: 1, 2 и 9. Каждое из этих цифр входит в состав арабского алфавита. Если мы представим числовую информацию в виде значения 89J1’4, то подобное значение будет некорректно обработано процессором и он выдаст исключение, то есть сгенерирует ошибку. Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.
Исполнителем является, в строгом приближении, процессор персонального компьютера. Например, число 129 состоит из трех цифр: 1, 2 и 9. Каждое из этих цифр входит в состав арабского алфавита. Если мы представим числовую информацию в виде значения 89J1’4, то подобное значение будет некорректно обработано процессором и он выдаст исключение, то есть сгенерирует ошибку. Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.
Приведенные два свойства являются ключевыми в алгоритмах кодирования числовой информации. Пожалуй, еще стоит отметить неосновное свойство – размер числа. Но в современном мире мощности персональных компьютеров постоянно увеличиваются и самые эффективные процессоры способы обрабатывать огромные значения.
Способы кодирования числовой информации
Сразу необходимо твердо уяснить следующее: процессор персонального компьютера взаимодействует с любыми данными исключительно на уровне цепочек, состоящих из 0 и 1. Набор нулей и единиц называют двоичным или бинарным кодом. То есть любые текстовые, символьные или числовые значения, которые понятны простому человеку, процессор преобразует в двоичный код. Следовательно, наша задача – научиться переводить числовые значения в бинарное представление, состоящее из цепочек 0 и 1.
Набор нулей и единиц называют двоичным или бинарным кодом. То есть любые текстовые, символьные или числовые значения, которые понятны простому человеку, процессор преобразует в двоичный код. Следовательно, наша задача – научиться переводить числовые значения в бинарное представление, состоящее из цепочек 0 и 1.
Для полного осознания алгоритма кодирования числовой информации необходимо очень хорошо уяснить понятие «Машинное слово». Возможно вы слышали, что иногда пользователи говорят, что на их компьютерах установлена 32-х разрядная или 64-х разрядная система Microsoft Windows. Именно значение разрядности (в приведенном примере это 32 или 64) и отвечает за то, сколько бит информации будет выделено для хранения какого-либо математического значения при кодировании числовой информации. То есть, если нам дано положительное целое число 25, то при преобразовании его в бинарный код, ему будет выделено 32 или 64 бита. Также напомню, что один байт информации состоит из 8 битов.
Далее по тексту я буду работать на уровне 16-и разрядной системы. То есть любое кодирование числовой информации будет представлено с использованием машинного слова в 16 бит.
Кодирование целых положительных чисел
Это наиболее простой способ кодирования данных, так как для его реализации необходимо уметь переводить числа из десятичной системы счисления в двоичную систему. Ниже я приведу таблицу, в которой покажу кодирование целых положительных чисел различной значности.
Исходное десятичное число | Закодированное десятичное число в двоичном коде |
5 | 0000 0000 0000 0101 |
27 | 0000 0000 0001 1011 |
870 | 0000 0011 0110 0110 |
19265 | 0100 1011 0100 0001 |
Очень внимательно посмотрите на вторую колонку данной таблицы. Как видно каждая закодированная цепочка, состоящая из нулей и единиц, имеет длину в 16 позиций. Для повышения читабельности я сгруппировал разряды на четыре группы по четыре бита в каждой группе.
Как видно каждая закодированная цепочка, состоящая из нулей и единиц, имеет длину в 16 позиций. Для повышения читабельности я сгруппировал разряды на четыре группы по четыре бита в каждой группе.
Нули, которые идут слева до первой единицы, считаются незначимыми, так как они не влияют на закодированное значение и при записи бинарного кода, например в тетрадь, они как правило не выписываются. То есть двоичное представление числа 5 обычно выписывают в формате 101. Но при этом вы должны обязательно понимать, с какой длиной машинного слова было выполнено данное преобразование. В нашем примере длина машинного слова составляет 16 бит.
Кодирование целых отрицательных чисел
Отрицательное число отличается от положительного только наличием специального символа ‘-‘, который ставится перед началом записи числового значения. Примеры отрицательных целых чисел: -20, -3, -189.
Наша задача – понять, каким образом процессор кодирует отрицательность числовых значений. Для этого нужно вспомнить, что такое старший разряд. Старший разряд – это самый левый разряд в записи двоичного числа. Именно данный разряд играет ключевую роль при кодировании отрицательных чисел.
Старший разряд – это самый левый разряд в записи двоичного числа. Именно данный разряд играет ключевую роль при кодировании отрицательных чисел.
Фундаментальное правило: старший или самый левый разряд числа при двоичном кодировании числовой информации отводится под знак числа, а остальные разряды под хранение самого значения числа. Если старший бит имеет значение 0 – показатель кодирования положительного числа, а если имеет значение 1 – показатель кодирования отрицательного числа. Все просто!
Ниже я приведу таблицу, в которой покажу кодирование целых отрицательных чисел различной значности:
Исходное десятичное число | Закодированное десятичное число в двоичном коде |
-5 | 1000 0000 0000 0101 |
-27 | 1000 0000 0001 1011 |
-870 | 1000 0011 0110 0110 |
-19265 | 1100 1011 0100 0001 |
Если пока все понятно, то двигаемся дальше!
Представьте, что перед вами лежит листок бумаги, на котором записан следующий бинарный код: 1000 0001 0100 0111 и вас просят назвать, какое десятичное число здесь закодировано. В первую очередь вам нужно посмотреть на значение старшего разряда. Видно, что оно равно 1. Вы делаете умозаключение, что этот бит показывает то, что перед вами отрицательное целое число. Сделав перевод в десятичную систему счисления вы получаете значение -327.
В первую очередь вам нужно посмотреть на значение старшего разряда. Видно, что оно равно 1. Вы делаете умозаключение, что этот бит показывает то, что перед вами отрицательное целое число. Сделав перевод в десятичную систему счисления вы получаете значение -327.
Но где гарантии, что перед вами не закодировано какое-то огромное положительное значение. Попробуйте взять число 33095 и перевести его в бинарное представление. После кодирования мы получаем значение 1000 0001 0100 0111 равное заданному, которое было записано на листке бумаги. Странно, не правда ли?!
То есть получается нельзя однозначно сказать, какое целое число закодировано набором 1000 0001 0100 0111? Мы только что с вами получили два различных значения: -327 и 33095. На самом деле можно! Для этого вам следует уточнить у автора задания следующую информацию: положительное или отрицательное число записано в представленном бинарном коде.
Парадоксальность ситуации заключается еще в том, что процессор персонального компьютера для хранения отрицательных целых чисел использует специальную форму представления. Чтобы получить бинарный код отрицательного целого числа необходимо прибегнуть к обратному и дополнительному коду чисел. В данной статье об дополнительном и обратном коде повествования не ведется. Также можно постулировать, что все выше проведенные выкладки, справедливы для прямого кода представления двоичных чисел.
Чтобы получить бинарный код отрицательного целого числа необходимо прибегнуть к обратному и дополнительному коду чисел. В данной статье об дополнительном и обратном коде повествования не ведется. Также можно постулировать, что все выше проведенные выкладки, справедливы для прямого кода представления двоичных чисел.
Если у вас остались какие-либо вопросы по кодированию числовой информации, то записывайтесь ко мне на индивидуальный урок по информатике. На данном уроке мы с вами дополнительно рассмотрим такие понятия, как: дополнительный код, обратный код, а также научимся кодировать дробные числовые величины.
Что такое двоичный?
Обновлено: 24.05.2020, Computer Hope
Двоичный может относиться к любому из следующего:
1. Двоичная — это система счисления с основанием 2 , изобретенная Готфридом Лейбницем, которая состоит только из двух чисел: 0 и 1. Эта система счисления является основой для всего двоичного кода , который используется для записи данные, такие как инструкции процессора компьютера, используемые каждый день.
Как работает двоичный код?
0 и 1 в двоичном формате обозначают ВЫКЛ или ВКЛ соответственно.В транзисторе «0» означает отсутствие потока электричества, а «1» означает, что электричеству разрешено течь. Таким образом, числа физически представлены внутри вычислительного устройства, что позволяет производить вычисления. Эта концепция дополнительно объясняется в нашем разделе о том, как читать двоичные числа.
Почему компьютеры используют двоичный код?
Двоичный код по-прежнему является основным языком для компьютеров по следующим причинам.
- Это простой и элегантный дизайн. Метод
- Binary 0 и 1 позволяет быстро обнаружить включенный или выключенный электрический сигнал.
- Положительные и отрицательные полюса магнитных носителей быстро переводятся в двоичную систему.
- Двоичный — самый эффективный способ управления логическими цепями.
Как читать двоичные числа
На следующей диаграмме показано двоичное число 01101000.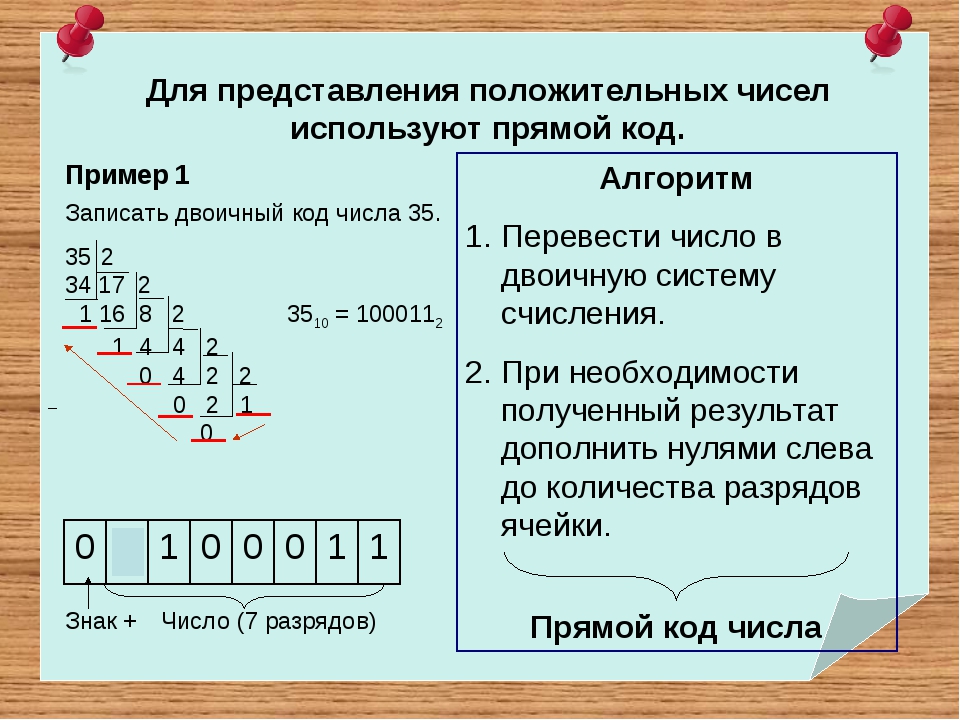 Каждый столбец представляет число два, возведенное в степень, причем значение этой экспоненты увеличивается на единицу при перемещении по каждой из восьми позиций. Чтобы получить общий результат этого примера, прочтите диаграмму от справа налево от и добавьте значение каждого столбца к предыдущему столбцу: (8 + 32 + 64) = 104.Как видите, мы не считаем биты с 0, потому что они «выключены».
Каждый столбец представляет число два, возведенное в степень, причем значение этой экспоненты увеличивается на единицу при перемещении по каждой из восьми позиций. Чтобы получить общий результат этого примера, прочтите диаграмму от справа налево от и добавьте значение каждого столбца к предыдущему столбцу: (8 + 32 + 64) = 104.Как видите, мы не считаем биты с 0, потому что они «выключены».
| Показатель степени: | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Значение: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| ВКЛ / ВЫКЛ: | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
Следующий пример — 11111111 в двоичном формате, максимальное 8-битное значение 255. Опять же, читая справа налево, мы получаем 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255.
Опять же, читая справа налево, мы получаем 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255.
| Значение: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| ВКЛ / ВЫКЛ: | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Подсчет на компьютере обычно начинается с «0» вместо «1».»Таким образом, подсчет всех бит равен 255, но если начать с 0, получится 256.
НаконечникЕсли вы возьмете двоичный код из первого примера (который составляет 104) и поместите его в ASCII, он выдаст строчные h . Чтобы написать слово hi , вам нужно будет добавить двоичное значение для буквы i , то есть 01101001. Соединяя эти два кода вместе, мы получаем 0110100001101001 или 104 и 105, что представляет hi .
Бинарный юмор
Изображение является примером бинарного юмора (шутки) через известную поговорку на многих футболках компьютерщиков. Те, кто умеет читать двоичный код, понимают, что эта цитата на самом деле говорит: «В мире всего двух типов людей : те, кто понимает двоичное, и те, кто не понимает». В двоичной системе 10 — это два , а не число десять .
Те, кто умеет читать двоичный код, понимают, что эта цитата на самом деле говорит: «В мире всего двух типов людей : те, кто понимает двоичное, и те, кто не понимает». В двоичной системе 10 — это два , а не число десять .
Преобразование текста в двоичный код
Следующий инструмент преобразует любой текст в двоичный.
2. Во время сеанса FTP двоичный — это команда, которая переключает режим передачи файлов на двоичный. Для получения информации о двоичных и других командах FTP см .: Как использовать FTP из командной строки?
3.При использовании в качестве существительного термин « binary » может относиться к исполняемому файлу. Например, «найдите двоичный файл с именем program.exe и дважды щелкните его».
База, BCD, .BIN, Двоичный файл, Бит, Десятичное, Шестнадцатеричное, Младший бит, Машинный язык, Старший бит, Родной язык, Отрицание, Полубайт, Восьмеричный, ВЫКЛ, ВКЛ, Кубит, Программные условия, Дополнение до двух
Двоичный кодировщик и переводчик декодера— LingoJam
Этот онлайн-инструмент позволяет кодировать текст в двоичный код и декодировать двоичный код обратно в текст. Просто вставьте свой текст в левое поле или свои двоичные данные в правое поле, и кодировщик / декодер мгновенно выдаст вам результат.
Просто вставьте свой текст в левое поле или свои двоичные данные в правое поле, и кодировщик / декодер мгновенно выдаст вам результат.
Что такое двоичный?
Информация (в техническом смысле) — это шаблон, который имеет определенный смысл. Есть много способов хранить информацию, но наиболее эффективный способ, которым компьютеры могут хранить информацию, — это шаблон из 2 разных символов. Мы используем символы «1» и «0» только потому, что это символы, которые мы все узнаем и которые в некотором смысле являются противоположностями друг друга (что-то vs.ничего). Но можно использовать любые символы. В двоичном формате важно то, что есть два символа (префикс «bi» в «двоичном» говорит нам об этом). Причина, по которой компьютеры любят говорить в двоичном формате, заключается в том, что компьютеры состоят из транзисторов, а транзисторы имеют два состояния.
Кодирование и декодирование текста
Преобразование между двоичным кодом и текстом довольно просто. Все обычные текстовые символы, которые вы видите на компьютерах, определены стандартом ASCII. Стандарт определяет 128 символов — все, что вы видите на стандартной английской клавиатуре, и еще немало.Каждому из этих символов присваивается номер от 0 до 127 (обратите внимание, что он идет только до 127, поскольку мы начинаем отсчет с 0, а не с 1).
Все обычные текстовые символы, которые вы видите на компьютерах, определены стандартом ASCII. Стандарт определяет 128 символов — все, что вы видите на стандартной английской клавиатуре, и еще немало.Каждому из этих символов присваивается номер от 0 до 127 (обратите внимание, что он идет только до 127, поскольку мы начинаем отсчет с 0, а не с 1).
Так как каждому из этих символов присвоен номер, мы можем писать текст в кодах ASCII:
«привет» —> «104 101 108 108 111»
Фактически, вот переводчик ASCII, который позволяет вам это сделать. Но мы хотим преобразовать в двоичный код , а не в коды ASCII, верно? Что ж, как оказывается, когда мы конвертируем текст в двоичный, мы — это , просто конвертируем текст в строку кодов ASCII, но мы также конвертируем эти коды ASCII в двоичные числа вместо десятичных чисел (числа, которые вы узнаете в школа).
Изучение того, как преобразовывать десятичные числа в двоичные числа, выходит за рамки этого объяснения, но вот преобразователь десятичного числа в двоичный, который объясняет процесс преобразования.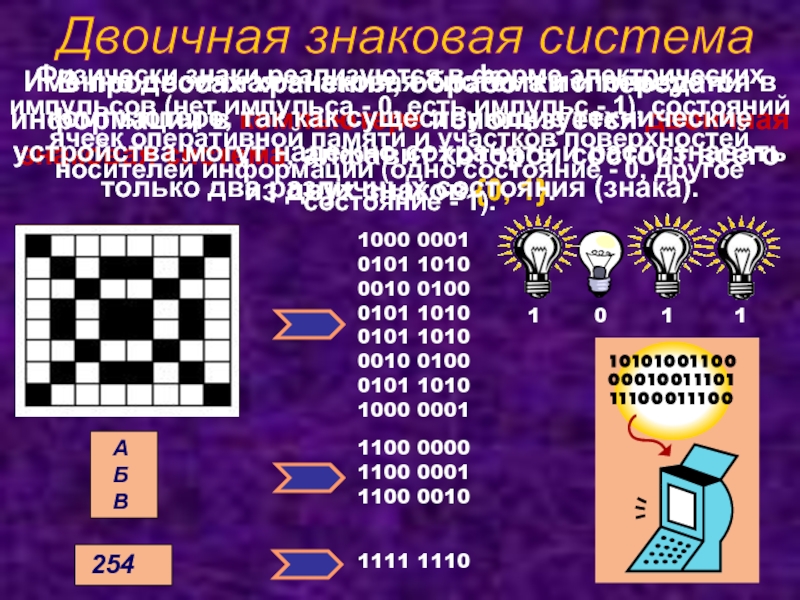 Итак, наконец, после преобразования десятичных кодов ASCII в двоичные коды ASCII мы получаем:
Итак, наконец, после преобразования десятичных кодов ASCII в двоичные коды ASCII мы получаем:
«привет» —> «0110100001100101011011000110110001101111»
Где каждое двоичное число имеет длину 8 бит, и все они сжаты в одну длинную строку.
Двоичное преобразование
Итак, вот оно.Этот переводчик может действовать как быстрый онлайн-кодировщик двоичного кода или двоичный декодер, так что вы можете переводить английский язык в двоичный и делиться закодированными сообщениями с друзьями. Затем они могут декодировать двоичное сообщение, используя тот же переводчик. Кто знает, если бы вы были достаточно посвящены изучению двоичных кодов ASCII, вы могли бы даже научиться писать в двоичном формате . Возможность преобразовывать двоичный код в текст в вашем мозгу довольно бессмысленна, но также довольно крута.
Я создал этот генератор двоичного кода днем, поэтому, если я могу что-то улучшить, дайте мне знать! Не стесняйтесь размещать странные двоичные сообщения в комментариях, чтобы другие люди могли их расшифровать! 🙂
↓ Подробнее.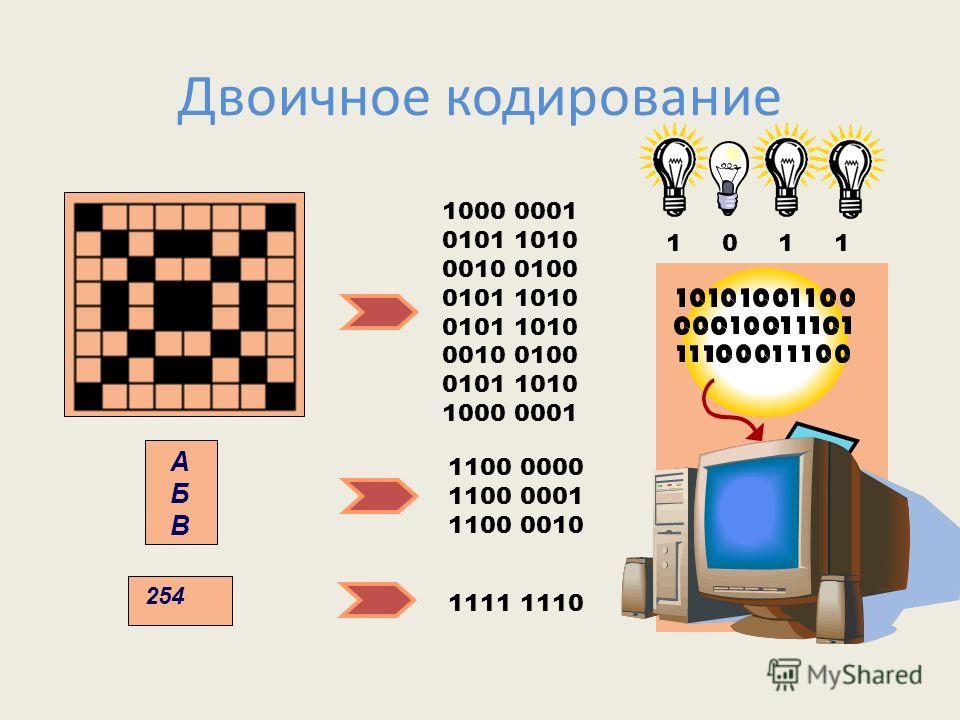 .. ↓
.. ↓
Почему компьютеры используют двоичные числа? Эссе
Двоичная система счисления, или система счисления с основанием 2, представляет числовые значения с использованием двух символов, 0 и 1. Более конкретно, обычная система счисления с основанием 2 представляет собой позиционную систему счисления с основанием 2. Из-за ее простой реализации в цифровой электронной схема с использованием логических вентилей, двоичная система используется внутри почти всех современных компьютеров.Почему в компьютерах используются двоичные числа
Двоичные числа, представляющие собой цепочки нулей и единиц, часто ассоциируются с компьютерами.Но почему это? Почему компьютеры не могут просто использовать основание 10 вместо преобразования в двоичный код и обратно? Разве не более эффективно использовать более высокое основание, поскольку двоичное (основание 2) представление использует больше «пробелов»?
Мне недавно задали этот вопрос кто-то, кто хорошо разбирается в компьютерах. Но этот вопрос также часто задают люди, не особо разбирающиеся в технологиях. В любом случае ответ довольно прост.
Но этот вопрос также часто задают люди, не особо разбирающиеся в технологиях. В любом случае ответ довольно прост.
Современный «цифровой» компьютер, в отличие от более старого «аналогового» компьютера, работает по принципу двух возможных состояний чего-либо — «включено» и «выключено».Это напрямую соответствует либо наличию электрического тока, либо его отсутствию. Состоянию «включено» присваивается значение «1», а состоянию «выключено» — значение «0».
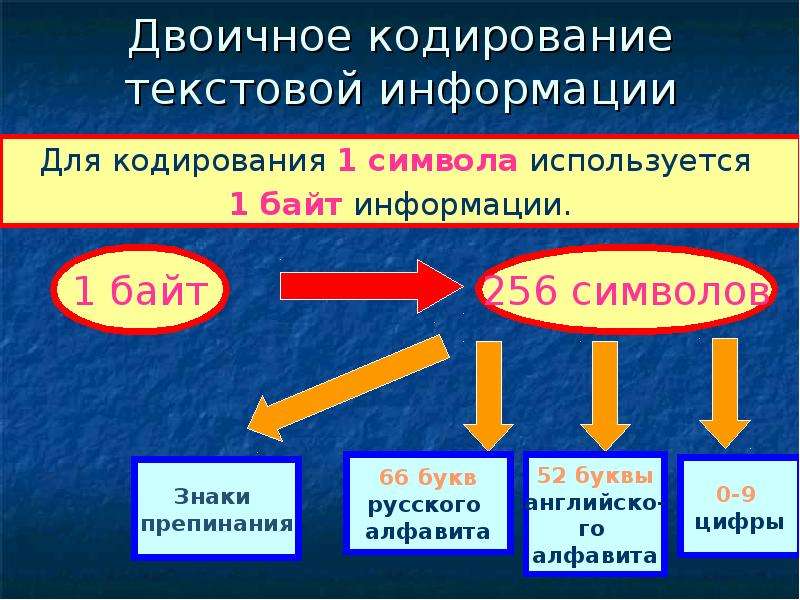
Термин «двоичный» подразумевает «два». Таким образом, двоичная система счисления — это система чисел, основанная на двух возможных цифрах — 0 и 1. Именно здесь вступают в силу строки двоичных цифр. Каждая двоичная цифра или «бит» представляет собой единичный 0 или 1, которые непосредственно соответствует одиночному «переключателю» в цепи.Сложите эти «переключатели» вместе, и вы сможете представить больше чисел. Таким образом, вместо 1 цифры вы получите 8, чтобы получить байт. (Байт, основная единица хранения, просто определяется как 8 бит; известные килобайты, мегабайты и гигабайты производятся из байта, и каждый из них в 1024 раза больше другого.


 . — — —
. — — — . —
. — 78 — действительное положительное число;
78 — действительное положительное число; Исполнителем является, в строгом приближении, процессор персонального компьютера. Например, число 129 состоит из трех цифр: 1, 2 и 9. Каждое из этих цифр входит в состав арабского алфавита. Если мы представим числовую информацию в виде значения 89J1’4, то подобное значение будет некорректно обработано процессором и он выдаст исключение, то есть сгенерирует ошибку. Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.
Исполнителем является, в строгом приближении, процессор персонального компьютера. Например, число 129 состоит из трех цифр: 1, 2 и 9. Каждое из этих цифр входит в состав арабского алфавита. Если мы представим числовую информацию в виде значения 89J1’4, то подобное значение будет некорректно обработано процессором и он выдаст исключение, то есть сгенерирует ошибку. Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.