Мега (M) → Кило (k), Метрические префиксы

Перевод величин: Мега (M) → Кило (k), Метрические префиксы

EN ES PT RU FR

Ой… Javascript не найден.

Увы, в вашем браузере отключен или не поддерживается JavaScript.

К сожалению, без JavaScript этот сайт работать не сможет. Проверьте настройки браузера, может быть JavaScript выключен случайно?

Перевод величин: мега (M) → кило (k), Метрические префиксы

?Настройки конвертера:

x

Объяснение настроек конвертера

Кстати, пользоваться настройками не обязательно. Вам вполне могут подойти настройки по умолчанию.

Количество значащих цифр

Для бытовых целей обычно не нужна высокая точность, удобнее получить округлённый результат. В таких случаях выберите 3 или 4 значащих цифры. Максимальная точность — 9 значащих цифр. Точность можно изменить в любой момент.

Разделитель групп разрядов

Выберите, в каком виде вам будет удобно получить результат:

1234567. 89	нет
1 234 567.89	пробел
1,234,567.89	запятая
1.234.567,89	точка

• Значащих цифр: 1  23456789
• Разделитель разрядов: нет  пробел  запятая  точка  

мега (M)

Метрические префиксы

кило (k)

Метрические префиксы

На этой странице мы можете сделать онлайновый перевод величин: мега → кило. Эти две единицы относятся к одной и той же системе измерения: Метрические префиксы.

Если вам нужен калькулятор для переводы из единицы мега в другую совместимую единицу, пожалуйста выберете нужную на этой странице ниже. Вы также можете переключиться на конвертер кило → мега.

Значения других единиц, равные введённым выше

» открыть »

» свернуть »

Единицы количества

мега → единица (1)
мега → пара
мега → тройка
мега → полдюжины
мега → декада
мега → дюжина
мега → чертова дюжина
мега → скор (англ. )
мега → флок (англ.)
мега → шок (англ.)
мега → сотня
мега → большая сотня (англ.)
мега → гросс
мега → тысяча
мега → большой гросс

Единицы: единица (1)  / пара  / тройка  / полдюжины  / декада  / дюжина  / чертова дюжина  / скор (англ.)  / флок (англ.)  / шок (англ.)  / сотня  / большая сотня (англ.)  / гросс  / тысяча  / большой гросс

» открыть »

» свернуть »

Проценты и доли

мега → процент (%)
мега → промилле (‰)
мега → частей на миллион (ppm)
мега → частей на миллиард (ppb)

Единицы: процент (%)  / промилле (‰)  / частей на миллион (ppm)  / частей на миллиард (ppb)

» открыть »

» свернуть »

Дроби

Внимание! Эта секция помогает ответить на вопросы такого типа: «Сколько 1/7-ых в одной половинке?» Чтобы получить ответ, введите 1 напротив 1/2 и посмотрите результат напротив 1/7.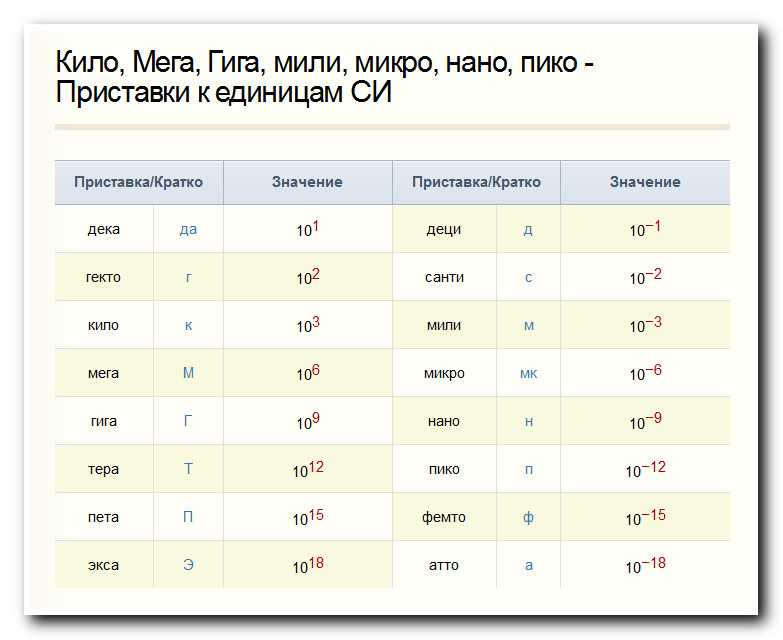 А теперь проверьте себя! Сможете при помощи нашего калькулятора быстро решить задачку: «Несколько одинаковых тортов разделили на 9 равных частей каждый, потом некоторые куски съели. Осталось 15 кусков. Если бы торты делили на 6 равных частей, и съели бы ровно такой же объём, сколько осталось бы кусков?». Наш калькулятор позволяет получить ответ в одно действие.

мега → половина (1/2)
мега → треть (1/3)
мега → четверть (1/4)
мега → одна пятая (1/5)
мега → одна шестая (1/6)
мега → одна седьмая (1/7)
мега → одна восьмая (1/8)
мега → одна девятая (1/9)
мега → одна десятая (1/10)
мега → одна шестнадцатая (1/16)
мега → одна тридцать вторая (1/32)

Единицы: половина (1/2)  / треть (1/3)  / четверть (1/4)  / одна пятая (1/5)  / одна шестая (1/6)  / одна седьмая (1/7)  / одна восьмая (1/8)  / одна девятая (1/9)  / одна десятая (1/10)  / одна шестнадцатая (1/16)  / одна тридцать вторая (1/32)

» открыть »

» свернуть »

Метрические префиксы

Эти префиксы широко используются в системе SI, могут применяться к любой единице.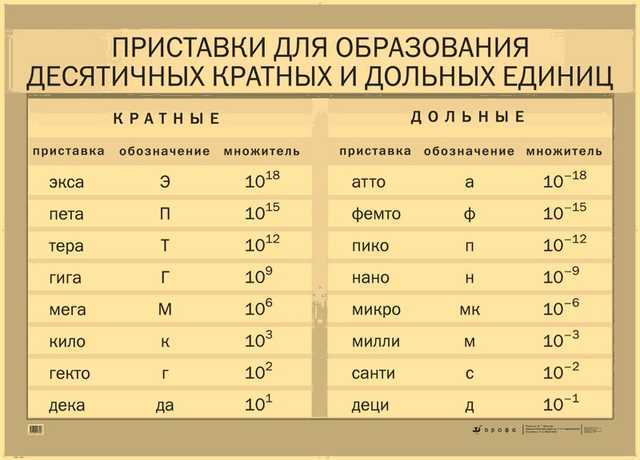

Например, килояблоко — это 1000 яблок.

мега → йокто (y)
мега → цепто (z)
мега → атто (a)
мега → фемто (f)
мега → пико (p)
мега → нано (n)
мега → микро (µ, mc)
мега → милли (m)
мега → санти (c)
мега → деци (d)
мега → дека (da)
мега → гекто (h)
мега → кило (k)
мега → мега (M)
мега → гига (G)
мега → тера (T)
мега → пета (P)
мега → экза (E)
мега → зетта (Z)
мега → йотта (Y)

Единицы: йокто (y)  / цепто (z)  / атто (a)  / фемто (f)  / пико (p)  / нано (n)  / микро (µ, mc)  / милли (m)  / санти (c)  / деци (d)  / дека (da)  / гекто (h)  / кило (k)  / мега (M)  / гига (G)  / тера (T)  / пета (P)  / экза (E)  / зетта (Z)  / йотта (Y)

» открыть »

» свернуть »

Количество выступающих

мега → солист
мега → дуэт
мега → трио
мега → квартет
мега → квинтет
мега → сикстет
мега → септет
мега → октет

Единицы: солист  / дуэт  / трио  / квартет  / квинтет  / сикстет  / септет  / октет

Не можете найти нужную единицу?

Попробуйте поискать:

Другие варианты:

Посмотрите алфавитный список всех единиц

Задайте вопрос на нашей странице в facebook

< Вернитесь к списку всех конвертеров

Надеемся, Вы смогли перевести все ваши величины, и Вам у нас на Convert-me. Com понравилось. Приходите снова!

 

 

! Значение единицы приблизительное.
Либо точного значения нет,
либо оно неизвестно. ? Пожалуйста, введите число. (?) Простите, неизвестное вещество. Пожалуйста, выберите что-то из списка. *** Нужно выбрать вещество.
От этого зависит результат.

Совет: Не можете найти нужную единицу? Попробуйте поиск по сайту. Поле для поиска в верхней части страницы.

Нашли ошибку? Хотите предложить дополнительные величины? Свяжитесь с нами в Facebook.

Действительно ли наш сайт существует с 1996 года? Да, это так. Первая версия онлайнового конвертера была сделана ещё в 1995, но тогда ещё не было языка JavaScript, поэтому все вычисления делались на сервере — это было медленно. А в 1996г была запущена первая версия сайта с мгновенными вычислениями.

Для экономии места блоки единиц могут отображаться в свёрнутом виде. Кликните по заголовку любого блока, чтобы свернуть или развернуть его.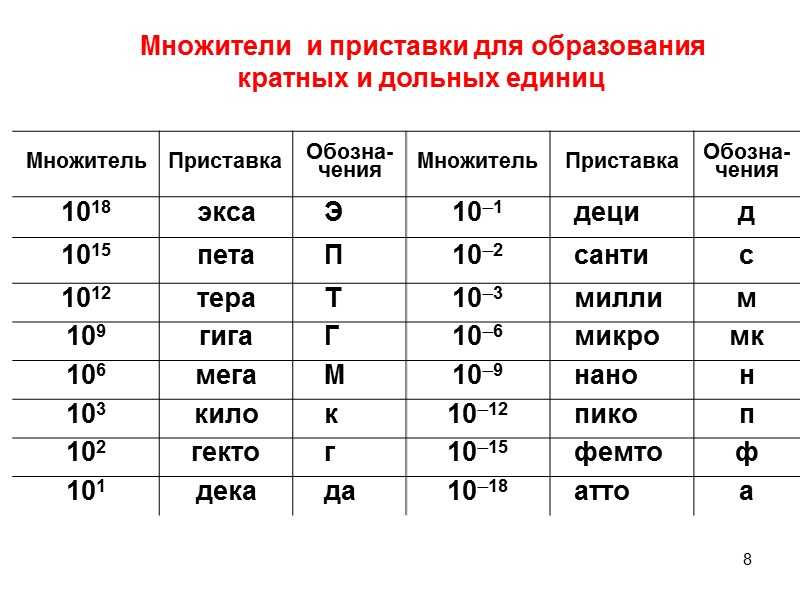

Слишком много единиц на странице? Сложно ориентироваться? Можно свернуть блок единиц — просто кликните по его заголовку. Второй клик развернёт блок обратно.

Наша цель — сделать перевод величин как можно более простой задачей. Есть идеи, как сделать наш сайт ещё удобнее? Поделитесь!

Минуточку, загружаем коэффициенты…

Как ПЕРЕВОДИТЬ единицы измерения ПРОСТО 🤔 ВСЕГО 3 правила

Краткий Курс школьной физики

СУПЕР АКЦИЯ!!!

Итак, прежде чем приступить к правилам перевода единиц измерения одной единицы измерения в другую, давайте посмотрим на две важные таблицы. В первой таблице приведены единицы измерения физических величин, которые используют в Системе СИ. Кстати, Система СИ особенно важна в физике. Поэтому, уделите ее изучению должное внимание.

Как вы понимаете, единиц измерения существует гораздо больше, чем указано в этой таблице. Остальные единицы измерения получают, добавляя приставки Системы СИ, которые представлены вот в этой таблице.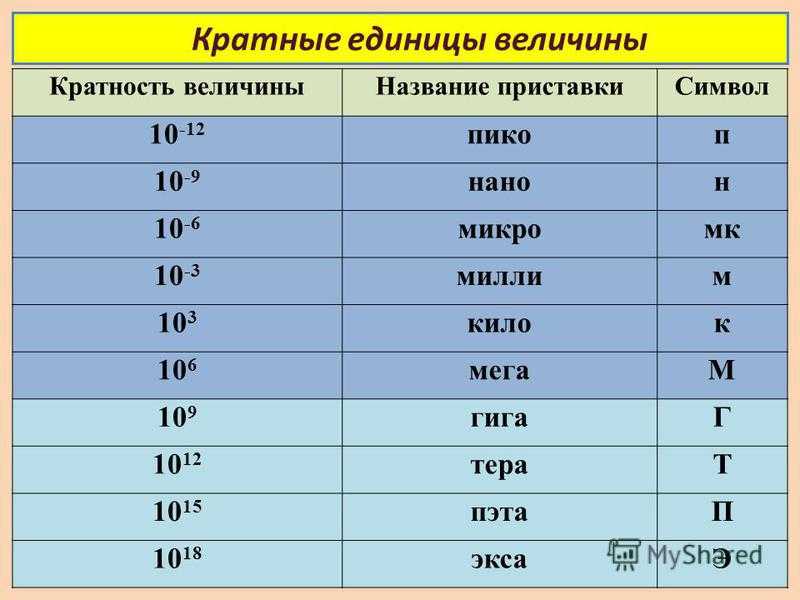

ВСЯ ГЕОМЕТРИЯ за 7 класс

ВСЯ ГЕОМЕТРИЯ за 8 класс

Как решать НЕРАВЕНСТВА

Так как переводить единицы измерения нужно часто, особенно в физике и математике (сантиметры в метры, миллиамперы в амперы и т.п.), и для их перевода нет никаких формул, то лучший способ научиться их переводить – вывести свои правила. Вот их мы с вами и рассмотрим. Таблицы у нас под рукой, значит, можем начинать.

Сначала рассмотрим Правило №1. По нему мы будем переводить в Систему СИ.

Здесь все просто. Приставку заменяем соответствующим множителем. Например, переведем единицы измерения длины: 2 километра (км) переведем в метры (м). Двойку просто переписываем и умножаем на множитель приставки «кило», который вы можете подсмотреть во второй таблице.

Еще один пример. Попробуем расчитать, сколько метров (м) в 5,3 сантиметров (см). 5,3 просто записываем и умножаем на множитель приставки «санти».

Теперь рассмотрим правило №2. Перевод единиц измерения из Системы СИ в другие единицы.

Здесь поступаем точно также, как по первому правилу, только у показателя степени меняем знак на противоположный. Например, 5 метров (м) перевести в километры (км). Пять так и записываем и умножаем на десять в минус третьей степени. Обратите внимание, что знак показателя мы поменяли на противоположный. 

Единицы измерения давления тоже можно перевести по нашим правилам. 6 паскалей (Па) переведем в килопаскали (кПа).

И напоследок рассмотрим Правило №3. Для тех, кому сложно сделать прямой перевод, например, «кило» в «мега» или «санти», можно сделать это в два этапа. Как переводить такие единицы измерения рассмотрим ниже.

Сначала нужно будет применить Правило №1, а затем Правило №2. Смотрите.

3 километра (км) переведем в сантиметры (см). После равно три так и записываем. По первому правилу переводим в метры. Значит, вместо приставки «кило» записываем множитель десять в степени три.

А теперь по второму правилу метры переводим в сантиметры, а, значит, умножаем на десять в степени два.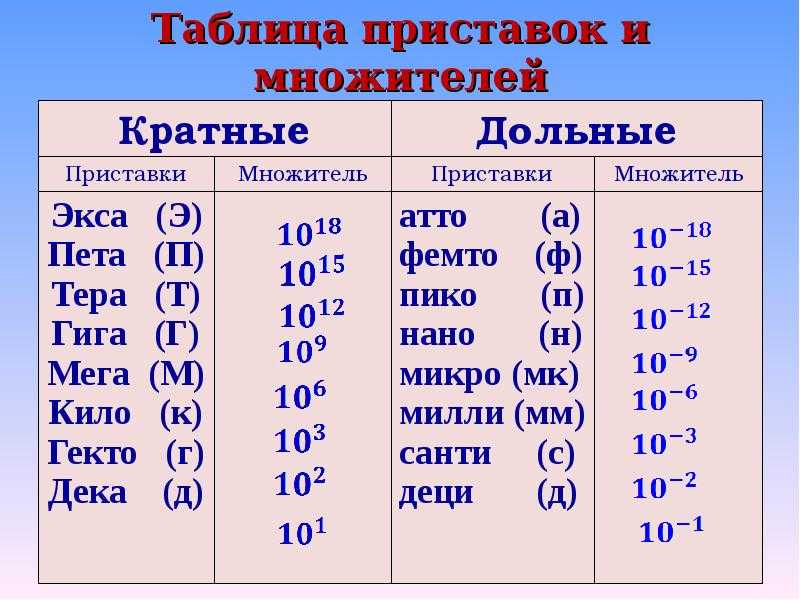 Не забываем менять знак показателя степени. Зная свойства степени, получаем три умножить на десять в пятой степени. Можно ответ оставить в таком виде, а можно записать так: триста тысяч сантиметров.

А теперь, еще немного потренируемся переводить единицы измерения, используя наши правила.

Для того, чтобы разобраться в этой теме более подробно, предлагаем посмотреть наш курс!

В нем мы научим вас переводить все единицы измерения, которые встречаются в физике и математике!

КУрс «Перевод единиц измерения»

В школе вам такое вряд ли расскажут…

Посмотреть бесплатный курс!

Конвертировать Единицы измерения / Конвертер единиц

Преобразуемое значение:

Калькулятор классических единиц измерения:

Категория измерения:Поглощенная дозаУскорениеКоличество веществаУголПлощадьБайты/БитыЕмкостьКаталитическая активностьВыброс CO2Скорость работы компьютера area productDose length productDynamic viscosityElectric chargeElectric conductanceElectric currentElectric dipole momentElectrical elastanceElectrical resistanceEnergyEquivalent doseFabric weight (Textiles)Font size (CSS)ForceFrequencyFuel consumptionIlluminanceImpulseInductanceIonizing radiation doseKinematic viscosityLuminanceLuminous energyLuminous fluxLuminous intensityMagnetic fieldMagnetic field strengthMagnetic fluxMagnetomotive forceMass / WeightMass flow rateMolar concentrationMolar massMolar volumeMusical intervalNumeral systemsOil equivalentParts-Per .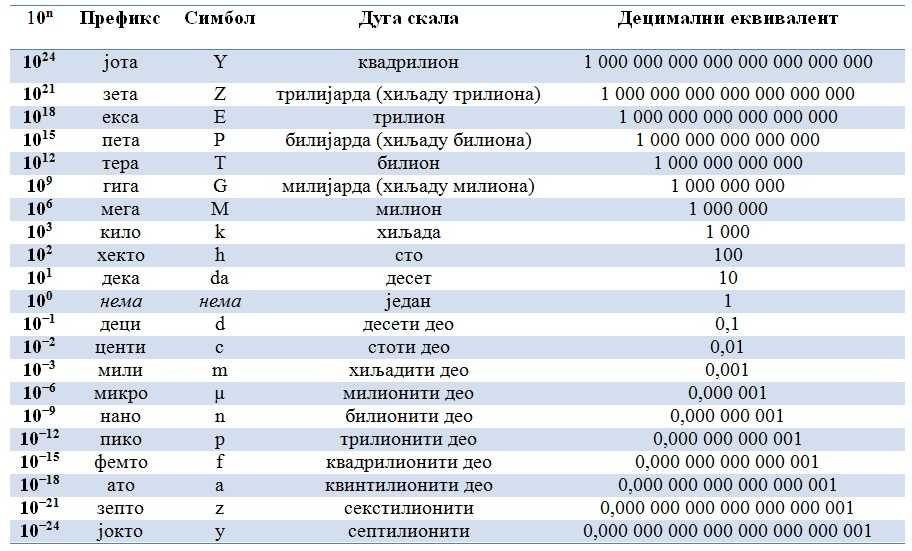 .. МощностьДавлениеДоза радиацииРадиоактивный ityСкорость вращенияSI-префиксыТвердый уголУровень звукаПоверхностное натяжениеТемператураИзмерение тканиВремяКрутящий моментСкоростьНапряжениеОбъемОбъемный расход   

Преобразуемое значение:

Исходная единица измерения: Ангстрем [Å]Астрономическая единица [AU]Аттометр [am]Длина кабеляСантиметр [см]Цепь [ch]Кубит (британский)Декаметр [dam]Дециметр [дм]FathomFemtometre [ fm]Фут [фут]ФурлонгГигаметр [Гм]Гектометр [чм]Дюйм [дюйм]Километр [км]Световые дниСветовые часыСветовые минутыСветовые секундыСветовые годыСсылкаМегаметр [Мм]Метр [м]Метрическая миляМикрометр [мкм] Мил — Тысяча миль (международная) [ми ]Миля (США)Миллиметр [мм]Нанометр [нм]Морская миляПарсек [ПК]ПершПиметр [pm]Планковая длинаПолюсКварталРимская миляСтатутная миляTwipX Единица — ЗигбанЯрды

Целевая единица: Ангстрем [Å] Астрономическая единица [AU] Аттометр [am] Длина кабеля Сантиметр [cm] Цепь [ch] Кубит (британский) Декаметр [dam] Дециметр [dm] Fathom Femtometre [fm] Foot [ft] Furlong Gigameter [Gm ]Гектометр [чм]Дюйм [дюйм]Километр [км]Световые дниСветовые часыСветовые минутыСветовые секундыСветовые годыСсылкаМегаметр [Мм]Метр [м]Метрическая миляМикрометр [мкм]Мил — ТысячаМиль (международная) [мили]Миля (США)Миллиметр [мм] Нанометр [нм]Морская миляПарсек [пк]ПершПиметр [пм]Планковая длинаПолюсКварталРимская миляСтатутная миляTwipX Единица — ЗигбанЯрды

Преобразование единиц измерения совсем не тривиально: Миллиметр, сантиметр, дециметр, метр, километр, мили, морской мили, футы, ярды, дюймы, локти, парсекы и световые годы. Со всеми эти измерения расстояний могут быть рассчитаны. И это даже не близкие ко всем возможным измерениям , вернее только самые распространенные те. В случае площадей (квадратный метр, квадратный километр, площадь, гектар, Морган, акр среди прочего), температуры (градусы Цельсия, Кельвина, по Фаренгейту), скорость (м/с, км/ч, мили/ч, узлы, мах), вес (сотни вес, килограмм, метрическая тонна, тонна США, имперская тонна, фунт и др.) и объемы (кубический метр, гектолитр, имперский галлон жидкости, галлон США жидкость, сухой галлон США, баррель среди прочего) не намного лучше. К полный хаос большинство из этих единицы также имеют подразделения и выше единиц (-> милли, санти, деци и др.). Короче: Хаос, в котором никто действительно, кажется, не видит ясно без помощи справки и различные формы помощи. Калькулятор для преобразования единиц измерения , подобный этому, идеально подходит для преобразования единиц измерения .

Преобразование — калькулятор в преобразование единиц измерения . Поддерживает огромное количество измерение единицы .

Мега в килограмм Конвертер

Введите значение

Введите значение

Вывод

Вывод

Сколько килограммов в мега?

---

Ответ: одна мега равна 1000 килограммам. Воспользуйтесь нашим онлайн-калькулятором перевода единиц измерения, чтобы перевести единицы из Мега в Килограммы. Просто введите значение 1 в Agate Line и посмотрите результат в килограммах.

Как конвертировать мега в килограммы (M в k)

---

Используя наш инструмент преобразования Мега в Кило, вы знаете, что одна Мега эквивалентна 1000 Кило. Следовательно, чтобы преобразовать мега в килограмм, нам просто нужно умножить число на 1000. Для этого мы будем использовать очень простую формулу преобразования мега в килограмм. См. приведенный ниже пример расчета.

Преобразовать 1 мега в килограмм ⇒ 1 мега = 1 × 1000 = 1000 килограмм

Что такое мега единица измерения?

---

Мега используется в качестве префикса в различных других единицах измерения для обозначения кратности конкретной единицы. Один мега равен 1e6.

Что такое символ Меги?

---

Мега символом является М. Это означает, что вы также можете записать одну Мега как 1 М.

Что такое килограмм?

---

Кило используется в качестве префикса в различных других единицах измерения для обозначения кратности конкретной единицы. Один килограмм равен 1000.

Какой символ у килограмма?

---

Символ килограмма — k. Это означает, что вы также можете записать один килограмм как 1 килобайт.

Таблица преобразования мегаграмм в килограммы

---

Mega [M]	Kilo [k]
1	1000
2	2000
3	3000
4	4000
5	5000
6	6000
7	7000
8	8000
9	9000
10	10000
100	100000
1000	1000000

Mega to Other Units Conversion Chart

---

Mega [M]	Выход
1 Мега в Йотте равен	1E-18
1 Мега в Zetta равен	1E-15
11110101 1E-15
111111111110101 1E-15
111111111111010102	1e-12
1 Mega in Peta is Equal to	1e-9
1 Mega in Tera is Equal to	0. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт